Template:Simulation Based Bounds: Difference between revisions
(Created page with '== Simulation Based Bounds == The SimuMatic tool in Weibull++ can be used to perform a large number of reliability analyses on data sets that have been created using Monte Carlo…') |
|||
| Line 3: | Line 3: | ||
The SimuMatic tool in Weibull++ can be used to perform a large number of reliability analyses on data sets that have been created using Monte Carlo simulation. This utility can assist the analyst to a) better understand life data analysis concepts, b) experiment with the influences of sample sizes and censoring schemes on analysis methods, c) construct simulation-based confidence intervals, d) better understand the concepts behind confidence intervals and e) design reliability tests. This section describes how to use simulation for estimating confidence bounds. <br> SimuMatic generates confidence bounds and assists in visualizing and understanding them. In addition, it allows one to determine the adequacy of certain parameter estimation methods (such as rank regression on X, rank regression on Y and maximum likelihood estimation) and to visualize the effects of different data censoring schemes on the confidence bounds. | The SimuMatic tool in Weibull++ can be used to perform a large number of reliability analyses on data sets that have been created using Monte Carlo simulation. This utility can assist the analyst to a) better understand life data analysis concepts, b) experiment with the influences of sample sizes and censoring schemes on analysis methods, c) construct simulation-based confidence intervals, d) better understand the concepts behind confidence intervals and e) design reliability tests. This section describes how to use simulation for estimating confidence bounds. <br> SimuMatic generates confidence bounds and assists in visualizing and understanding them. In addition, it allows one to determine the adequacy of certain parameter estimation methods (such as rank regression on X, rank regression on Y and maximum likelihood estimation) and to visualize the effects of different data censoring schemes on the confidence bounds. | ||
'''Example 4''' | |||
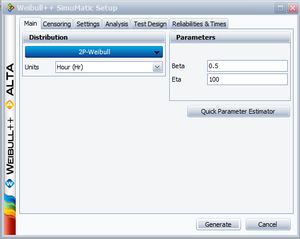
The purpose of this example is to determine the best parameter estimation method for a sample of ten units following a Weibull distribution with <math>\beta =2</math> and <math>\eta =100</math> and with complete time-to-failure data for each unit (i.e. no censoring). The number of generated data sets is set to 10,000. The SimuMatic inputs are shown next. | The purpose of this example is to determine the best parameter estimation method for a sample of ten units following a Weibull distribution with <math>\beta =2</math> and <math>\eta =100</math> and with complete time-to-failure data for each unit (i.e. no censoring). The number of generated data sets is set to 10,000. The SimuMatic inputs are shown next. | ||
Revision as of 23:09, 9 February 2012
Simulation Based Bounds
The SimuMatic tool in Weibull++ can be used to perform a large number of reliability analyses on data sets that have been created using Monte Carlo simulation. This utility can assist the analyst to a) better understand life data analysis concepts, b) experiment with the influences of sample sizes and censoring schemes on analysis methods, c) construct simulation-based confidence intervals, d) better understand the concepts behind confidence intervals and e) design reliability tests. This section describes how to use simulation for estimating confidence bounds.
SimuMatic generates confidence bounds and assists in visualizing and understanding them. In addition, it allows one to determine the adequacy of certain parameter estimation methods (such as rank regression on X, rank regression on Y and maximum likelihood estimation) and to visualize the effects of different data censoring schemes on the confidence bounds.
Example 4
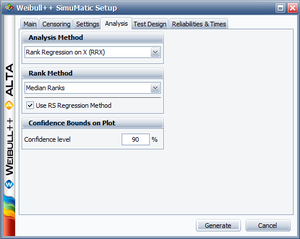
The purpose of this example is to determine the best parameter estimation method for a sample of ten units following a Weibull distribution with [math]\displaystyle{ \beta =2 }[/math] and [math]\displaystyle{ \eta =100 }[/math] and with complete time-to-failure data for each unit (i.e. no censoring). The number of generated data sets is set to 10,000. The SimuMatic inputs are shown next.
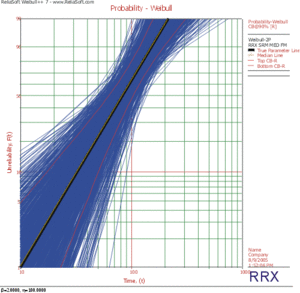
The parameters are estimated using RRX, RRY and MLE. The plotted results generated by SimuMatic are shown next.
- Using RRX:
- Using RRY:
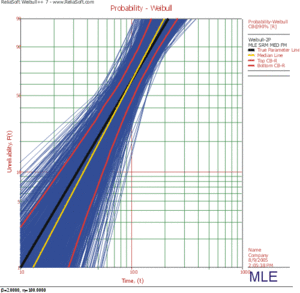
- Using MLE:
The results clearly demonstrate that the median RRX estimate provides the least deviation from the truth for this sample size and data type. However, the MLE outputs are grouped more closely together, as evidenced by the bounds. The previous figures also show the simulation-based bounds, as well as the expected variation due to sampling error.
This experiment can be repeated in SimuMatic using multiple censoring schemes (including Type I and Type II right censoring as well as random censoring) with various distributions. Multiple experiments can be performed with this utility to evaluate assumptions about the appropriate parameter estimation method to use for data sets.