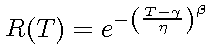Weibull++ Standard Folio Data 1P-Weibull: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 14: | Line 14: | ||
<math>\gamma=0 \,\!</math> and assuming <math>\beta=C=Constant \,\!</math> assumed value or: | <math>\gamma=0 \,\!</math> and assuming <math>\beta=C=Constant \,\!</math> assumed value or: | ||
[[Image:weibullreliabilityfunction. | [[Image:weibullreliabilityfunction.gif]] | ||
where the only unknown parameter is the scale parameter, <math>\eta\,\!</math>. | where the only unknown parameter is the scale parameter, <math>\eta\,\!</math>. | ||
Revision as of 21:21, 7 February 2012
The One-Parameter Weibull DistributionThe one-parameter Weibull reliability function is obtained by again setting [math]\displaystyle{ \gamma=0 \,\! }[/math] and assuming [math]\displaystyle{ \beta=C=Constant \,\! }[/math] assumed value or: where the only unknown parameter is the scale parameter, [math]\displaystyle{ \eta\,\! }[/math]. Note that in the formulation of the one-parameter Weibull, we assume that the shape parameter [math]\displaystyle{ \beta \,\! }[/math] is known a priori from past experience on identical or similar products. The advantage of doing this is that data sets with few or no failures can be analyzed.
|
| The Weibull Distribution |