Template:One parameter exponential distribution example Probability Plot: Difference between revisions
m (moved Template:One parameter exponential distribution example to Template:One parameter exponential distribution example 1: Make the name match the book) |
No edit summary |
||
| Line 1: | Line 1: | ||
====Example 1: One Parameter Exponential Example==== | ====Example 1: One Parameter Exponential Example RRY==== | ||
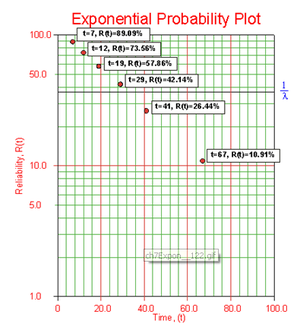
Six units are put on a life test and tested to failure. The failure times are 7, 12, 19, 29, 41, and 67 hours. Estimate the failure rate parameter for a one-parameter exponential distribution using the probability plotting method. | Six units are put on a life test and tested to failure. The failure times are 7, 12, 19, 29, 41, and 67 hours. Estimate the failure rate parameter for a one-parameter exponential distribution using the probability plotting method. | ||
Revision as of 23:35, 6 February 2012
Example 1: One Parameter Exponential Example RRY
Six units are put on a life test and tested to failure. The failure times are 7, 12, 19, 29, 41, and 67 hours. Estimate the failure rate parameter for a one-parameter exponential distribution using the probability plotting method.
Solution to Example 1
In order to plot the points for the probability plot, the appropriate reliability estimate values must be obtained. These will be equivalent to [math]\displaystyle{ 100%-MR }[/math], since the y-axis represents the reliability and the [math]\displaystyle{ MR }[/math] values represent unreliability estimates.
Next, these points are plotted on exponential probability plotting paper. A sample of this type of plotting paper is shown next, with the sample points in place. Notice how these points describe a line with a negative slope.
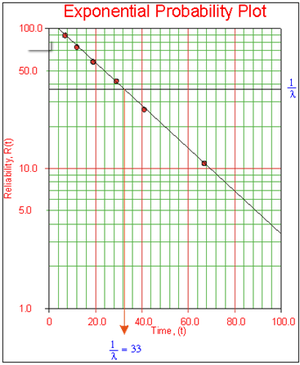
Once the points are plotted, draw the best possible straight line through these points. The time value at which this line intersects with a horizontal line drawn at the 36.8% reliability mark is the mean life, and the reciprocal of this is the failure rate [math]\displaystyle{ \lambda }[/math].
This is because at [math]\displaystyle{ t=m=\tfrac{1}{\lambda } }[/math]:
- [math]\displaystyle{ \begin{align} R(t)= & {{e}^{-\lambda \cdot t}} \\ R(t)= & {{e}^{-\lambda \cdot \tfrac{1}{\lambda }}} \\ R(t)= & {{e}^{-1}}=0.368=36.8%. \end{align} }[/math]
These steps are shown graphically in the next pages.
As can be seen in the plot below, the best-fit line through the data points crosses the [math]\displaystyle{ R=36.8% }[/math] line at [math]\displaystyle{ t=33 }[/math] hours.
Since [math]\displaystyle{ \tfrac{1}{\lambda }=33 }[/math] hours, [math]\displaystyle{ \lambda =0.0303 }[/math] failures/hour.