The Logistic Distribution

The Logistic Distribution

The logistic distribution has been used for growth models, and is used in a certain type of regression known as the logistic regression. It has also applications in modeling life data. The shape of the logistic distribution and the normal distribution are very similar [27]. There are some who argue that the logistic distribution is inappropriate for modeling lifetime data because the left-hand limit of the distribution extends to negative infinity. This could conceivably result in modeling negative times-to-failure. However, provided that the distribution in question has a relatively high mean and a relatively small location parameter, the issue of negative failure times should not present itself as a problem.

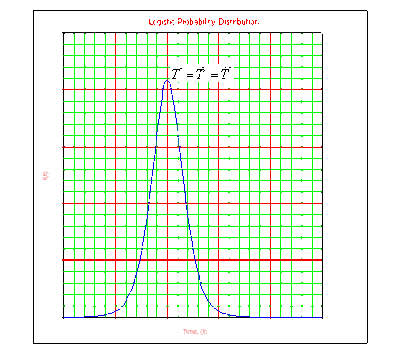
Logistic Probability Density Function

The logistic [math]\displaystyle{ pdf }[/math] is given by:

[math]\displaystyle{ \begin{matrix} f(T)=\tfrac{{{e}^{z}}}{\sigma {{(1+{{e}^{z}})}^{2}}} \\ z=\tfrac{t-\mu }{\sigma } \\ -\infty \lt T\lt \infty ,\ \ -\infty \lt \mu \lt \infty ,\sigma \gt 0 \\ \end{matrix} }[/math]

where:

[math]\displaystyle{ \begin{align} \mu = & \text{location parameter (also denoted as }\overline{T)} \\ \sigma = & \text{scale parameter} \end{align} }[/math]

The Logistic Mean, Median and Mode

The logistic mean or MTTF is actually one of the parameters of the distribution, usually denoted as [math]\displaystyle{ \mu }[/math] . Since the logistic distribution is symmetrical, the median and the mode are always equal to the mean, [math]\displaystyle{ \mu =\tilde{T}=\breve{T}. }[/math]

The Logistic Standard Deviation

The standard deviation of the logistic distribution, [math]\displaystyle{ {{\sigma }_{T}} }[/math] , is given by:

[math]\displaystyle{ {{\sigma }_{T}}=\sigma \pi \frac{\sqrt{3}}{3} }[/math]

The Logistic Reliability Function

The reliability for a mission of time [math]\displaystyle{ T }[/math] , starting at age 0, for the logistic distribution is determined by:

[math]\displaystyle{ R(T)=\int_{T}^{\infty }f(t)dt }[/math]

or:

[math]\displaystyle{ R(T)=\frac{1}{1+{{e}^{z}}} }[/math]

The unreliability function is:

[math]\displaystyle{ F=\frac{{{e}^{z}}}{1+{{e}^{z}}} }[/math]

where:

[math]\displaystyle{ z=\frac{T-\mu }{\sigma } }[/math]

The Logistic Conditional Reliability Function

The logistic conditional reliability function is given by:

[math]\displaystyle{ R(t/T)=\frac{R(T+t)}{R(T)}=\frac{1+{{e}^{\tfrac{T-\mu }{\sigma }}}}{1+{{e}^{\tfrac{t+T-\mu }{\sigma }}}} }[/math]

The Logistic Reliable Life

The logistic reliable life is given by:

[math]\displaystyle{ {{T}_{R}}=\mu +\sigma [\ln (1-R)-\ln (R)] }[/math]

The Logistic Failure Rate Function

The logistic failure rate function is given by:

[math]\displaystyle{ \lambda (T)=\frac{{{e}^{z}}}{\sigma (1+{{e}^{z}})} }[/math]

Characteristics of the Logistic Distribution

• The logistic distribution has no shape parameter. This means that the logistic [math]\displaystyle{ pdf }[/math] has only one shape, the bell shape, and this shape does not change. The shape of the logistic distribution is very similar to that of the normal distribution.

• The mean, [math]\displaystyle{ \mu }[/math] , or the mean life or the [math]\displaystyle{ MTTF }[/math] , is also the location parameter of the logistic [math]\displaystyle{ pdf }[/math] , as it locates the [math]\displaystyle{ pdf }[/math] along the abscissa. It can assume values of [math]\displaystyle{ -\infty \lt \bar{T}\lt \infty }[/math] .

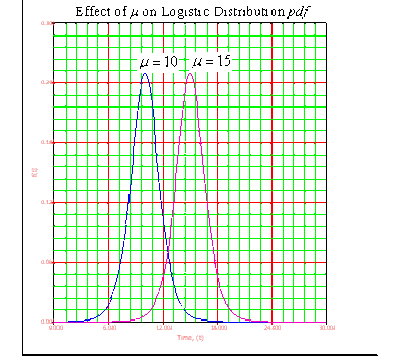
• As [math]\displaystyle{ \mu }[/math] decreases, the [math]\displaystyle{ pdf }[/math] is shifted to the left.

• As [math]\displaystyle{ \mu }[/math] increases, the [math]\displaystyle{ pdf }[/math] is shifted to the right.

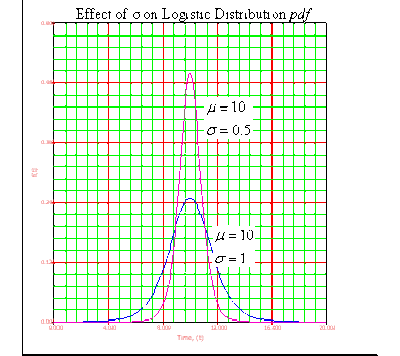
• As [math]\displaystyle{ \sigma }[/math] decreases, the [math]\displaystyle{ pdf }[/math] gets pushed toward the mean, or it becomes narrower and taller.

• As [math]\displaystyle{ \sigma }[/math] increases, the [math]\displaystyle{ pdf }[/math] spreads out away from the mean, or it becomes broader and shallower.

• The scale parameter can assume values of [math]\displaystyle{ 0\lt \sigma \lt \infty }[/math].

• The logistic [math]\displaystyle{ pdf }[/math] starts at [math]\displaystyle{ T=-\infty }[/math] with an [math]\displaystyle{ f(T)=0 }[/math] . As [math]\displaystyle{ T }[/math] increases, [math]\displaystyle{ f(T) }[/math] also increases, goes through its point of inflection and reaches its maximum value at [math]\displaystyle{ T=\bar{T} }[/math] . Thereafter, [math]\displaystyle{ f(T) }[/math] decreases, goes through its point of inflection and assumes a value of [math]\displaystyle{ f(T)=0 }[/math] at [math]\displaystyle{ T=+\infty }[/math] .

• For [math]\displaystyle{ T=\pm \infty , }[/math] the [math]\displaystyle{ pdf }[/math] equals [math]\displaystyle{ 0. }[/math] The maximum value of the [math]\displaystyle{ pdf }[/math] occurs at [math]\displaystyle{ T }[/math] = [math]\displaystyle{ \mu }[/math] and equals [math]\displaystyle{ \tfrac{1}{4\sigma }. }[/math]

• The point of inflection of the [math]\displaystyle{ pdf }[/math] plot is the point where the second derivative of the [math]\displaystyle{ pdf }[/math] equals zero. The inflection point occurs at [math]\displaystyle{ T=\mu +\sigma \ln (2\pm \sqrt{3}) }[/math] or [math]\displaystyle{ T\approx \mu \pm \sigma 1.31696 }[/math].

• If the location parameter [math]\displaystyle{ \mu }[/math] decreases, the reliability plot is shifted to the left. If [math]\displaystyle{ \mu }[/math] increases, the reliability plot is shifted to the right.

• If [math]\displaystyle{ T=\mu }[/math] then [math]\displaystyle{ R=0.5 }[/math] . is the inflection point. If [math]\displaystyle{ T\lt \mu }[/math] then [math]\displaystyle{ R(t) }[/math] is concave (concave down); if [math]\displaystyle{ T\gt \mu }[/math] then [math]\displaystyle{ R(t) }[/math] is convex (concave up). For [math]\displaystyle{ T\lt \mu , }[/math] [math]\displaystyle{ \lambda (t) }[/math] is convex (concave up), for [math]\displaystyle{ T\gt \mu ; }[/math] [math]\displaystyle{ \lambda (t) }[/math] is concave (concave down).

• The main difference between the normal distribution and logistic distribution lies in the tails and in the behavior of the failure rate function. The logistic distribution has slightly longer tails compared to the normal distribution. Also, in the upper tail of the logistic distribution, the failure rate function levels out for large [math]\displaystyle{ t }[/math] approaching 1/ [math]\displaystyle{ \delta . }[/math]

• If location parameter [math]\displaystyle{ \mu }[/math] decreases, the failure rate plot is shifted to the left. Vice versa if [math]\displaystyle{ \mu }[/math] increases, the failure rate plot is shifted to the right.

• [math]\displaystyle{ \lambda }[/math] always increases. For [math]\displaystyle{ T\to -\infty }[/math] for [math]\displaystyle{ T\to \infty }[/math] It is always [math]\displaystyle{ 0\le \lambda (t)\le \tfrac{1}{\sigma }. }[/math]

• If [math]\displaystyle{ \sigma }[/math] increases, then [math]\displaystyle{ \lambda (t) }[/math] increases more slowly and smoothly. The segment of time where [math]\displaystyle{ 0\lt \lambda (t)\lt \tfrac{1}{\sigma } }[/math] increases, too, whereas the region where [math]\displaystyle{ \lambda (t) }[/math] is close to [math]\displaystyle{ 0 }[/math] or [math]\displaystyle{ \tfrac{1}{\sigma } }[/math] gets narrower. Conversely, if [math]\displaystyle{ \sigma }[/math] decreases, then [math]\displaystyle{ \lambda (t) }[/math] increases more quickly and sharply. The segment of time where [math]\displaystyle{ 0\lt }[/math] [math]\displaystyle{ \lambda (t)\lt \tfrac{1}{\sigma } }[/math] decreases, too, whereas the region where [math]\displaystyle{ \lambda (t) }[/math] is close to [math]\displaystyle{ 0 }[/math] or [math]\displaystyle{ \tfrac{1}{\sigma } }[/math] gets broader.

Weibull++ Notes on Negative Time Values

One of the disadvantages of using the logistic distribution for reliability calculations is the fact that the logistic distribution starts at negative infinity. This can result in negative values for some of the results. Negative values for time are not accepted in most of the components of Weibull++, nor are they implemented. Certain components of the application reserve negative values for suspensions, or will not return negative results. For example, the Quick Calculation Pad will return a null value (zero) if the result is negative. Only the Free-Form (Probit) data sheet can accept negative values for the random variable (x-axis values).

Probability Paper

The form of the Logistic probability paper is based on linearizing the [math]\displaystyle{ cdf }[/math] . From Eqn. (UnR fcn), [math]\displaystyle{ z }[/math] can be calculated as a function of the [math]\displaystyle{ cdf }[/math] [math]\displaystyle{ F }[/math] as follows:

[math]\displaystyle{ z=\ln (F)-\ln (1-F) }[/math]

or using Eqn. (z func of parameters)

[math]\displaystyle{ \frac{T-\mu }{\sigma }=\ln (F)-\ln (1-F) }[/math]

Then:

[math]\displaystyle{ \ln (F)-\ln (1-F)=-\frac{\mu }{\sigma }+\frac{1}{\sigma }T }[/math]

Now let:

[math]\displaystyle{ y=\ln (F)-\ln (1-F) }[/math]

[math]\displaystyle{ x=T }[/math]

and:

[math]\displaystyle{ a=-\frac{\mu }{\sigma } }[/math]

[math]\displaystyle{ b=\frac{1}{\sigma } }[/math]

which results in the following linear equation:

[math]\displaystyle{ y=a+bx }[/math]

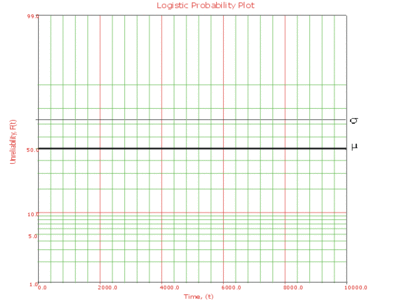
The logistic probability paper resulting from this linearized [math]\displaystyle{ cdf }[/math] function is shown next.

Since the logistic distribution is symmetrical, the area under the [math]\displaystyle{ pdf }[/math] curve from [math]\displaystyle{ -\infty }[/math] to [math]\displaystyle{ \mu }[/math] is [math]\displaystyle{ 0.5 }[/math] , as is the area from [math]\displaystyle{ \mu }[/math] to [math]\displaystyle{ +\infty }[/math] . Consequently, the value of [math]\displaystyle{ \mu }[/math] is said to be the point where [math]\displaystyle{ R(t)=Q(t)=50% }[/math] . This means that the estimate of [math]\displaystyle{ \mu }[/math] can be read from the point where the plotted line crosses the 50% unreliability line.

For [math]\displaystyle{ z=1 }[/math] , [math]\displaystyle{ \sigma =t-\mu }[/math] and [math]\displaystyle{ R(t)=\tfrac{1}{1+\exp (1)}\approx 0.2689. }[/math] Therefore, [math]\displaystyle{ \sigma }[/math] can be found by subtracting [math]\displaystyle{ \mu }[/math] from the time value where the plotted probability line crosses the 73.10% unreliability (26.89% reliability) horizontal line.

Confidence Bounds

In this section, we present the methods used in the application to estimate the different types of confidence bounds for logistically distributed data. The complete derivations were presented in detail (for a general function) in Chapter 5.

Bounds on the Parameters

The lower and upper bounds on the location parameter [math]\displaystyle{ \widehat{\mu } }[/math] are estimated from

[math]\displaystyle{ {{\mu }_{U}}=\widehat{\mu }+{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })\text{ }}\text{ (upper bound)} }[/math]

[math]\displaystyle{ {{\mu }_{L}}=\widehat{\mu }-{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })\text{ }}\text{ (lower bound)} }[/math]

The lower and upper bounds on the scale parameter [math]\displaystyle{ \widehat{\sigma } }[/math] are estimated from:

[math]\displaystyle{ {{\sigma }_{U}}=\widehat{\sigma }{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\sigma })\text{ }}}{\widehat{\sigma }}}}(\text{upper bound}) }[/math]

[math]\displaystyle{ {{\sigma }_{L}}=\widehat{\sigma }{{e}^{\tfrac{-{{K}_{\alpha }}\sqrt{Var(\widehat{\sigma })\text{ }}}{\widehat{\sigma }}}}\text{ (lower bound)} }[/math]

where [math]\displaystyle{ {{K}_{\alpha }} }[/math] is defined by:

[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }}) }[/math]

If [math]\displaystyle{ \delta }[/math] is the confidence level, then [math]\displaystyle{ \alpha =\tfrac{1-\delta }{2} }[/math] for the two-sided bounds, and [math]\displaystyle{ \alpha =1-\delta }[/math] for the one-sided bounds.

The variances and covariances of [math]\displaystyle{ \widehat{\mu } }[/math] and [math]\displaystyle{ \widehat{\sigma } }[/math] are estimated from the Fisher matrix, as follows:

[math]\displaystyle{ \left( \begin{matrix} \widehat{Var}\left( \widehat{\mu } \right) & \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right) \\ \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right) & \widehat{Var}\left( \widehat{\sigma } \right) \\ \end{matrix} \right)=\left( \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\mu }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \mu \partial \sigma } \\ {} & {} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial \mu \partial \sigma } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }^{2}}} \\ \end{matrix} \right)_{\mu =\widehat{\mu },\sigma =\widehat{\sigma }}^{-1} }[/math]

[math]\displaystyle{ \Lambda }[/math] is the log-likelihood function of the normal distribution, described in Chapter 3 and Appendix C.

Bounds on Reliability

The reliability of the logistic distribution is:

[math]\displaystyle{ \widehat{R}=\frac{1}{1+{{e}^{\widehat{z}}}} }[/math]

where:

[math]\displaystyle{ \widehat{z}=\frac{T-\widehat{\mu }}{\widehat{\sigma }} }[/math]

Here [math]\displaystyle{ -\infty \lt T\lt \infty }[/math] , [math]\displaystyle{ -\infty \lt \mu \lt \infty }[/math] , [math]\displaystyle{ 0\lt \sigma \lt \infty }[/math] . Therefore, [math]\displaystyle{ z }[/math] also is changing from [math]\displaystyle{ -\infty }[/math] to [math]\displaystyle{ +\infty }[/math] . Then the bounds on [math]\displaystyle{ z }[/math] are estimated from:

[math]\displaystyle{ {{z}_{U}}=\widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})\text{ }} }[/math]

[math]\displaystyle{ {{z}_{L}}=\widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})\text{ }}\text{ } }[/math]

where:

[math]\displaystyle{ Var(\widehat{z})={{(\frac{\partial z}{\partial \mu })}^{2}}Var(\widehat{\mu })+2(\frac{\partial z}{\partial \mu })(\frac{\partial z}{\partial \sigma })Cov(\widehat{\mu },\widehat{\sigma })+{{(\frac{\partial z}{\partial \sigma })}^{2}}Var(\widehat{\sigma }) }[/math]

or:

[math]\displaystyle{ Var(\widehat{z})=\frac{1}{{{\sigma }^{2}}}(Var(\widehat{\mu })+2\widehat{z}Cov(\widehat{\mu },\widehat{\sigma })+{{\widehat{z}}^{2}}Var(\widehat{\sigma })) }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ {{R}_{U}}=\frac{1}{1+{{e}^{{{z}_{L}}}}}\text{(upper bound)} }[/math]

[math]\displaystyle{ {{R}_{L}}=\frac{1}{1+{{e}^{{{z}_{U}}}}}\text{(lower bound)} }[/math]

Bounds on Time

The bounds around time for a given logistic percentile (unreliability) are estimated by first solving the reliability equation with respect to time as follows:

[math]\displaystyle{ \widehat{T}(\widehat{\mu },\widehat{\sigma })=\widehat{\mu }+\widehat{\sigma }z }[/math]

where:

[math]\displaystyle{ z=\ln (1-R)-\ln (R) }[/math]

[math]\displaystyle{ Var(\widehat{T})={{(\frac{\partial T}{\partial \mu })}^{2}}Var(\widehat{\mu })+2(\frac{\partial T}{\partial \mu })(\frac{\partial T}{\partial \sigma })Cov(\widehat{\mu },\widehat{\sigma })+{{(\frac{\partial T}{\partial \sigma })}^{2}}Var(\widehat{\sigma }) }[/math]

or:

[math]\displaystyle{ Var(\widehat{T})=Var(\widehat{\mu })+2\widehat{z}Cov(\widehat{\mu },\widehat{\sigma })+{{\widehat{z}}^{2}}Var(\widehat{\sigma }) }[/math]

The upper and lower bounds are then found by:

[math]\displaystyle{ {{T}_{U}}=\widehat{T}+{{K}_{\alpha }}\sqrt{Var(\widehat{T})\text{ }}(\text{upper bound}) }[/math]

[math]\displaystyle{ {{T}_{L}}=\widehat{T}-{{K}_{\alpha }}\sqrt{Var(\widehat{T})\text{ }}(\text{lower bound}) }[/math]

A Logistic Distribution Example

The lifetime of a mechanical valve is known to follow a logistic distribution. Ten units were tested for 28 months and the following months-to-failure data was collected.

[math]\displaystyle{ \overset{{}}{\mathop{\text{Table 10}\text{.1 - Times-to-Failure Data with Suspensions}}}\, }[/math] [math]\displaystyle{ \begin{matrix} \text{Data Point Index} & \text{State F or S} & \text{State End Time} \\ \text{1} & \text{F} & \text{8} \\ \text{2} & \text{F} & \text{10} \\ \text{3} & \text{F} & \text{15} \\ \text{4} & \text{F} & \text{17} \\ \text{5} & \text{F} & \text{19} \\ \text{6} & \text{F} & \text{26} \\ \text{7} & \text{F} & \text{27} \\ \text{8} & \text{S} & \text{28} \\ \text{9} & \text{S} & \text{28} \\ \text{10} & \text{S} & \text{28} \\ \end{matrix} }[/math]

• Determine the valve's design life if specifications call for a reliability goal of 0.90.

• The valve is to be used in a pumping device that requires 1 month of continuous operation. What is the probability of the pump failing due to the valve?

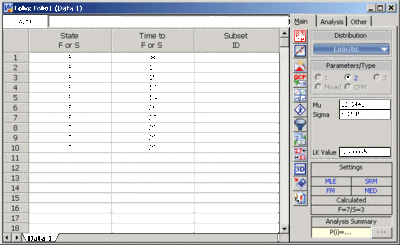
This data set can be entered into Weibull++ as follows:

The computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{align} & \widehat{\mu }= & 22.34 \\ & \hat{\sigma }= & 6.15 \end{align} }[/math]

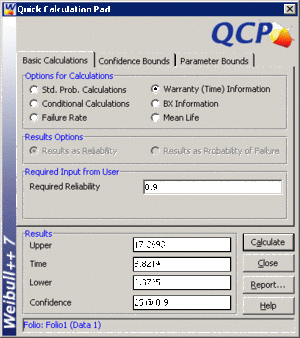
• The valve's design life, along with 90% two sided confidence bounds, can be obtained using the QCP as follows:

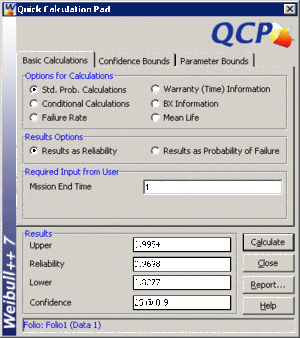
• The probability, along with 90% two sided confidence bounds, that the pump fails due to a valve failure during the first month is obtained as follows: