Failure Discounting: Difference between revisions
No edit summary |
|||
| Line 33: | Line 33: | ||
<br> | <br> | ||
<br> | <br> | ||
Table A.1 - Launch sequence with failure modes and failure values | :::Table A.1 - Launch sequence with failure modes and failure values | ||
<br> | |||
Launch Result/ | {|style= align="center" border="1" | ||
!Launch Number | |||
1 F1 1.000 | !Result/Mode | ||
2 F2 1.000 1.000 | !Failure 1 | ||
3 F3 0.900 1.000 1.000 | !Failure 2 | ||
4 S 0.684 0.900 1.000 | !Failure 3 | ||
5 F2 0.536 1.000 0.900 1.000 | !Failure 4 | ||
6 F3 0.438 1.000 1.000 1.000 1.000 | !Failure 5 | ||
7 S 0.369 0.900 1.000 0.900 1.000 | !Failure 6 | ||
8 S 0.319 0.684 0.900 0.684 0.900 | !Failure 7 | ||
9 S 0.280 0.536 0.684 0.536 0.684 | !Sum of Failures | ||
10 S 0.250 0.438 0.536 0.438 0.536 | |- | ||
11 S 0.226 0.369 0.438 0.369 0.438 | |1|| F1|| 1.000|| || || || || || || 1.000 | ||
12 S 0.206 0.319 0.369 0.319 0.369 | |- | ||
13 S 0.189 0.280 0.319 0.280 0.319 | |2|| F2|| 1.000|| 1.000 || || || || || || 2.000 | ||
14 S 0.175 0.250 0.280 0.250 0.280 | |- | ||
15 S 0.162 0.226 0.250 0.226 0.250 | |3|| F3|| 0.900|| 1.000|| 1.000|| || || || || 2.900 | ||
16 S 0.152 0.206 0.226 0.206 0.226 | |- | ||
17 F4 0.142 0.189 0.206 0.189 0.206 1.000 | |4|| S|| 0.684|| 0.900|| 1.000|| || || || || 2.584 | ||
18 S 0.134 0.175 0.189 0.175 0.189 1.000 | |- | ||
19 F5 0.127 0.162 0.175 0.162 0.175 0.900 1.000 2.701 | |5|| F2|| 0.536|| 1.000|| 0.900|| 1.000|| || || || 3.436 | ||
20 S 0.120 0.152 0.162 0.152 0.162 0.684 1.000 2.432 | |- | ||
21 S 0.114 0.142 0.152 0.142 0.152 0.536 0.900 2.138 | |6|| F3|| 0.438|| 1.000|| 1.000|| 1.000|| 1.000|| || || 4.438 | ||
22 S 0.109 0.134 0.142 0.134 0.142 0.438 0.684 1.783 | |- | ||
|7|| S|| 0.369|| 0.900|| 1.000|| 0.900|| 1.000|| || || 4.169 | |||
|- | |||
|8|| S|| 0.319|| 0.684|| 0.900|| 0.684|| 0.900|| || || 3.486 | |||
|- | |||
|9|| S|| 0.280|| 0.536|| 0.684|| 0.536|| 0.684|| || || 2.720 | |||
|- | |||
|10|| S|| 0.250|| 0.438|| 0.536|| 0.438|| 0.536|| || || 2.197 | |||
|- | |||
|11|| S|| 0.226|| 0.369|| 0.438|| 0.369|| 0.438|| || || 1.839 | |||
|- | |||
|12|| S|| 0.206|| 0.319|| 0.369|| 0.319|| 0.369|| || || 1.581 | |||
|- | |||
|13|| S|| 0.189|| 0.280|| 0.319|| 0.280|| 0.319|| || || 1.387 | |||
|- | |||
|14|| S|| 0.175|| 0.250|| 0.280|| 0.250|| 0.280|| || || 1.235 | |||
|- | |||
|15|| S|| 0.162|| 0.226|| 0.250|| 0.226|| 0.250|| || || 1.114 | |||
|- | |||
|16|| S|| 0.152|| 0.206|| 0.226|| 0.206|| 0.226|| || || 1.014 | |||
|- | |||
|17|| F4|| 0.142|| 0.189|| 0.206|| 0.189|| 0.206|| 1.000|| || 1.931 | |||
|- | |||
|18|| S|| 0.134|| 0.175|| 0.189|| 0.175|| 0.189|| 1.000|| || 1.861 | |||
|- | |||
|19|| F5|| 0.127|| 0.162|| 0.175|| 0.162|| 0.175|| 0.900|| 1.000|| 2.701 | |||
|- | |||
|20|| S|| 0.120|| 0.152|| 0.162|| 0.152|| 0.162|| 0.684|| 1.000|| 2.432 | |||
|- | |||
|21|| S|| 0.114|| 0.142|| 0.152|| 0.142|| 0.152|| 0.536|| 0.900|| 2.138 | |||
|- | |||
|22|| S|| 0.109|| 0.134|| 0.142|| 0.134|| 0.142|| 0.438|| 0.684|| 1.783 | |||
|} | |||
Revision as of 17:48, 19 July 2011
Failure Discounting
During a reliability growth test, once a failure has been analyzed and corrective actions for that specific failure mode have been implemented, the probability of its recurrence is diminished [4]. Then for the success/failure data that follow, the value of the failure for which corrective actions have already been implemented should be subtracted from the total number of failures. But certain questions arise, such as, To what extent should the failure value be diminished or discounted? and How should the failure value be defined? One answer would be to use engineering judgment, e.g. a panel of specialists would agree that the probability of failure has been reduced by [math]\displaystyle{ 50% }[/math] or [math]\displaystyle{ 90% }[/math] and therefore that failure should be given a value of 0.5 or 0.9. The obvious disadvantage of this approach is its arbitrariness and the difficulty of reaching an agreement. Therefore, a statistical basis is selected, one that is repeatable and less arbitrary. Failure discounting is applied when using the Lloyd-Lipow, Logistic and the Standard and Modified Gompertz models.
The value of the failure, [math]\displaystyle{ f }[/math] , is chosen to be the upper confidence limit on the probability of failure based on the number of successful tests following implementation of the corrective action. The failure value is given by the following equation:
- [math]\displaystyle{ f=1-{{(1-CL)}^{\tfrac{1}{{{S}_{n}}}}} }[/math]
where:
- [math]\displaystyle{ \begin{align} & CL= & \text{the confidence level}\text{.} \\ & {{S}_{n}}= & \text{the number of successful tests after the first success } \\ & & \text{following the corrective action}\text{.} \end{align} }[/math]
For example, after one successful test following a corrective action, [math]\displaystyle{ {{S}_{n}}=1 }[/math] , the failure is given a value of 0.9 based on a [math]\displaystyle{ 90% }[/math] confidence level. After two successful tests, [math]\displaystyle{ {{S}_{n}}=2 }[/math] , the failure is given a value of 0.684, and so on. The procedure for applying this method is illustrated in the next example.
Example
Use failure discounting to answer the questions below. Assume that during the 22 launches given in Table A.1, the first failure was caused by Mode 1, the second and fourth failures were caused by Mode 2, the third and fifth failures were caused by Mode 3, the sixth failure was caused by Mode 4 and the seventh failure was caused by Mode 5.
1) Find the Standard Gompertz reliability growth curve using the results of the first 15 launches.
2) Find the predicted reliability after launch 22.
3) Calculate the reliability after launch 22 based on the full data set from Table A.2 and compare with the estimate obtained for question 2.
- Table A.1 - Launch sequence with failure modes and failure values
| Launch Number | Result/Mode | Failure 1 | Failure 2 | Failure 3 | Failure 4 | Failure 5 | Failure 6 | Failure 7 | Sum of Failures |
|---|---|---|---|---|---|---|---|---|---|
| 1 | F1 | 1.000 | 1.000 | ||||||
| 2 | F2 | 1.000 | 1.000 | 2.000 | |||||
| 3 | F3 | 0.900 | 1.000 | 1.000 | 2.900 | ||||
| 4 | S | 0.684 | 0.900 | 1.000 | 2.584 | ||||
| 5 | F2 | 0.536 | 1.000 | 0.900 | 1.000 | 3.436 | |||
| 6 | F3 | 0.438 | 1.000 | 1.000 | 1.000 | 1.000 | 4.438 | ||
| 7 | S | 0.369 | 0.900 | 1.000 | 0.900 | 1.000 | 4.169 | ||
| 8 | S | 0.319 | 0.684 | 0.900 | 0.684 | 0.900 | 3.486 | ||
| 9 | S | 0.280 | 0.536 | 0.684 | 0.536 | 0.684 | 2.720 | ||
| 10 | S | 0.250 | 0.438 | 0.536 | 0.438 | 0.536 | 2.197 | ||
| 11 | S | 0.226 | 0.369 | 0.438 | 0.369 | 0.438 | 1.839 | ||
| 12 | S | 0.206 | 0.319 | 0.369 | 0.319 | 0.369 | 1.581 | ||
| 13 | S | 0.189 | 0.280 | 0.319 | 0.280 | 0.319 | 1.387 | ||
| 14 | S | 0.175 | 0.250 | 0.280 | 0.250 | 0.280 | 1.235 | ||
| 15 | S | 0.162 | 0.226 | 0.250 | 0.226 | 0.250 | 1.114 | ||
| 16 | S | 0.152 | 0.206 | 0.226 | 0.206 | 0.226 | 1.014 | ||
| 17 | F4 | 0.142 | 0.189 | 0.206 | 0.189 | 0.206 | 1.000 | 1.931 | |
| 18 | S | 0.134 | 0.175 | 0.189 | 0.175 | 0.189 | 1.000 | 1.861 | |
| 19 | F5 | 0.127 | 0.162 | 0.175 | 0.162 | 0.175 | 0.900 | 1.000 | 2.701 |
| 20 | S | 0.120 | 0.152 | 0.162 | 0.152 | 0.162 | 0.684 | 1.000 | 2.432 |
| 21 | S | 0.114 | 0.142 | 0.152 | 0.142 | 0.152 | 0.536 | 0.900 | 2.138 |
| 22 | S | 0.109 | 0.134 | 0.142 | 0.134 | 0.142 | 0.438 | 0.684 | 1.783 |
Table A.2 - Comparison of the predicted reliability with the actual data
Launch Calculated Gompertz Number Reliability (%) ln(R) Reliability (%) 1 0.000 2 0.000 3 3.333 1.204
4 35.406 3.567 16.426 5 31.283 3.443 26.691 6 26.039 3.260 37.858 7 40.442 3.670 48.691 8 56.422 4.033 58.363 9 69.783 4.245 66.496 [math]\displaystyle{ {{S}_{1}} }[/math] = 22.218 10 78.029 4.357 73.044 11 83.281 4.422 78.155 12 86.824 4.464 82.055 13 89.331 4.492 84.983 14 91.175 4.513 87.155 15 92.573 4.528 88.754 [math]\displaystyle{ {{S}_{2}} }[/math] = 26.776 16 93.660 4.540 89.923 17 88.639 4.484 90.774 18 89.661 4.496 91.392 19 85.787 4.452 91.839 20 87.841 4.476 92.163 21 89.820 4.498 92.396 [math]\displaystyle{ {{S}_{3}} }[/math] = 26.946 22 91.896 4.521 92.565
Solution
1) Table A.1 is organized as follows:
• Each failure is represented by a single column and named Failure 1, Failure 2 etc. The failure mode for each failure is shown in the Result/Mode column where is also incidated in the launch is a success.
• The values of failure are calculated from Eqn. (att4) and are based on [math]\displaystyle{ CL=0.90 }[/math] .
• These values are summed and the reliability is calculated from:
- [math]\displaystyle{ R=\left[ 1-\left( \frac{\mathop{}_{i=1}^{N}{{f}_{i}}}{n} \right) \right]\cdot 100\text{ }% }[/math]
where [math]\displaystyle{ N }[/math] is the number of failures and [math]\displaystyle{ n }[/math] is the number of events, tests, runs or launches.
• Failure 1 is Mode 1; it occurs at launch 1 and it does not recur throughout the process.
So at launch 3, [math]\displaystyle{ {{S}_{n}}=1 }[/math] , and so on.
• Failure 2 is Mode 2; it occurs at launch 2 and it recurs at launch 5. Therefore, [math]\displaystyle{ {{S}_{n}}=1 }[/math] at launch 4 and at launch 7, and so on.
• Failure 3 is Mode 3; it occurs at launch 3 and it recurs at launch 6. Therefore, [math]\displaystyle{ {{S}_{n}}=1 }[/math] at launch 5 and at launch 8, and so on.
• Failure 6 is Mode 4; it occurs at launch 17 and it does not recur throughout the process. So at launch 19, [math]\displaystyle{ {{S}_{n}}=1 }[/math] , and so on.
• Failure 7 is Mode 5; it occurs at launch 19 and it does not recur throughout the process. So at launch 21, [math]\displaystyle{ {{S}_{n}}=1 }[/math] , and so on.
For launch 3 and failure 1, [math]\displaystyle{ {{S}_{n}}=1 }[/math] in Eqn. (att4).
- [math]\displaystyle{ {{f}_{1/3}}=1-{{(1-0.90)}^{1/1}}=0.900 }[/math]
For launch 4 and failure 1, [math]\displaystyle{ {{S}_{n}}=2 }[/math] in Eqn. (att4).
- [math]\displaystyle{ {{f}_{1/4}}=1-{{(1-0.90)}^{1/2}}=0.684 }[/math]
And so on.
Calculate the initial values of the Gompertz parameters using Table A.2. Based on the equations from Chapter 7, the initial values are:
Now, since the initial values have been determined, the Gauss-Newton method can be used. Substituting [math]\displaystyle{ {{Y}_{i}}={{R}_{i}}, }[/math] [math]\displaystyle{ g_{1}^{(0)}=89.31, }[/math] [math]\displaystyle{ g_{2}^{(0)}=0.127, }[/math] [math]\displaystyle{ g_{3}^{(0)}=0.578 }[/math] . The iterations are continued to solve for the parameters. Using RGA, the estimators of the parameters for the given example are:
- [math]\displaystyle{ \begin{align} & \widehat{a}= & 0.9299 \\ & \widehat{b}= & 0.0943 \\ & \widehat{c}= & 0.7170 \end{align} }[/math]
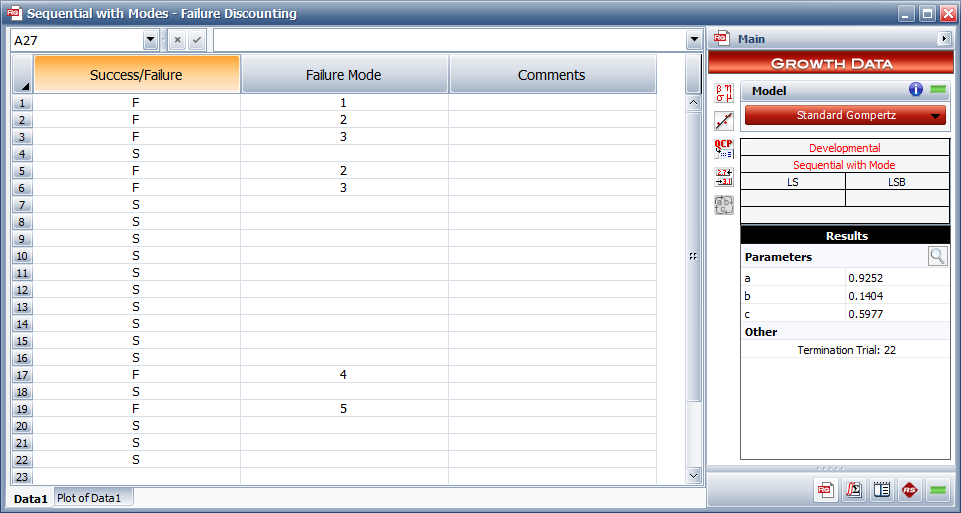
Figure entered data Standard GMP shows the entered data and the estimated parameters.
The Gompertz reliability growth curve may now be written as follows where [math]\displaystyle{ {{L}_{G}} }[/math] is the number of launches with the first successful launch being counted as [math]\displaystyle{ {{L}_{G}}=1 }[/math] . Therefore, [math]\displaystyle{ {{L}_{G}} }[/math] is equal to 19, since reliability growth starts with launch 4.
- [math]\displaystyle{ R=0.9299{{(0.0943)}^{{{0.7170}^{{{L}_{G}}}}}} }[/math]
- Figure A.1: Entered data and the estimated Standard Gompertz parameters.
2) Based on Eqn. (predictR), the predicted reliability after launch 22 is:
- [math]\displaystyle{ \begin{align} & R= & 0.9299{{(0.0943)}^{{{0.7170}^{19}}}} \\ & = & 0.9260 \end{align} }[/math]
The predicted reliability after launch 22 is calculated using the Quick Calculation Pad and is shown in Figure A1.
3) In Table A.2, the predicted reliability values, as calculated from Eqn. (predictR), are compared with the reliabilities that are calculated from the raw data using failure discounting. It can be seen in Table A.2 and in Figure oldfig34 that the Gompertz curve appears to provide a good fit to the actual data.