This example compares the results for the Arrhenius-Lognormal model with interval data.
Reference Case
The data set is from Example 19.11 on page 508 in the book Statistical Methods for Reliability Data by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998.
Data
The data set for a new-technology IC Device is given below.
| Number in Group |
Last Inspected (Hr) |
State F/S |
Time to State |
Temperature (K)
|
| 50 |
788 |
S |
1536 |
423.15
|
| 50 |
788 |
S |
1536 |
448.15
|
| 50 |
96 |
S |
96 |
473.15
|
| 1 |
384 |
F |
788 |
523.15
|
| 3 |
788 |
F |
1536 |
523.15
|
| 5 |
1536 |
F |
2304 |
523.15
|
| 41 |
1536 |
S |
2304 |
523.15
|
| 4 |
192 |
F |
384 |
573.15
|
| 27 |
384 |
F |
788 |
573.15
|
| 16 |
788 |
F |
1536 |
573.15
|
| 3 |
788 |
S |
1536 |
573.15
|
Result
The following function is used for the Ln-Mean [math]\displaystyle{ \mu'\,\! }[/math] of the lognormal distribution:
- [math]\displaystyle{ \mu' = \beta_{0}+\beta_{1} \times \frac{11605}{T}\,\! }[/math]
where T is the temperature; [math]\displaystyle{ \beta_{1}\,\! }[/math] is the activation energy; 11605 is calculated from the reciprocal of the Boltzmann constant. This function can be written in the following way:
- [math]\displaystyle{ e^{\mu'} = e^{\alpha_{0}+ \frac {\alpha_{1}}{T}}\,\! }[/math]
The above equation is the general log-linear model in ALTA. In ALTA, the coefficients are denoted by [math]\displaystyle{ \alpha_{i}\,\! }[/math]. We can see [math]\displaystyle{ \beta_{0} = \alpha_{0}\,\! }[/math] and [math]\displaystyle{ \beta_{1} = \frac{\alpha_{1}}{11605}\,\! }[/math].
In fact, the above model also can be expressed using the traditional Arrhenius model:
- [math]\displaystyle{ e^{\mu'} = e^{\alpha_{0}+ \frac {\alpha_{1}}{T}} = C \times e^{\frac{B}{T}}\,\! }[/math]
In the book, the following results are provided:
- ML estimations for the model parameters are: [math]\displaystyle{ \sigma\,\! }[/math] = 0.52, [math]\displaystyle{ \beta_{0}\,\! }[/math] = -10.2, [math]\displaystyle{ \beta_{1}\,\! }[/math] = 0.83, ([math]\displaystyle{ \alpha_{1}\,\! }[/math] = [math]\displaystyle{ \beta_{1}\times \,\! }[/math] 11605 = 9632.15).
- The standard deviation of each parameter: [math]\displaystyle{ std(\sigma)\,\! }[/math] = 0.06, [math]\displaystyle{ std(\beta_{0})\,\! }[/math] = 1.5, [math]\displaystyle{ std(\beta_{1})\,\! }[/math] = 0.07. Therefore, their variances are: [math]\displaystyle{ Var(\sigma)\,\! }[/math] = 0.0036, [math]\displaystyle{ Var(\beta_{0})\,\! }[/math] = 2.25, [math]\displaystyle{ Var(\beta_{1})\,\! }[/math] = 0.0049. In terms of [math]\displaystyle{ \alpha_{1}\,\! }[/math] , the variance is [math]\displaystyle{ Var(\alpha_{1})\,\! }[/math] = 116052 and [math]\displaystyle{ Var(\beta_{1})\,\! }[/math] = 659912.5.
- The 95% two-sided confidence bounds are: for [math]\displaystyle{ \sigma\,\! }[/math] it is [0.42, 0.64]; for [math]\displaystyle{ \beta_{0}\,\! }[/math] it is [-13.2, -7.2]; for [math]\displaystyle{ \beta_{1}\,\! }[/math] it is [0.68, 0.97]. In terms of [math]\displaystyle{ \alpha_{1}\,\! }[/math], the bounds are [7891.14, 11256.85].
- The log-likelihood value is -88.26.
- Common shape parameter test result: the likelihood ratio common shape parameter test statistic is 4.7. It is larger than the critical value 3.84. This indicates that there is some lack of fit in the constant [math]\displaystyle{ \sigma\,\! }[/math] assumption across all the stress levels.
Results in ALTA
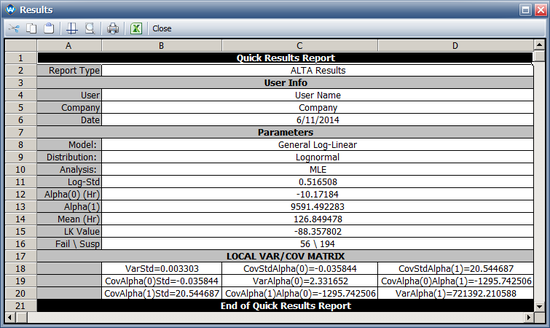
- The following picture shows the ML estimations for the model parameters in ALTA and the log-likelihood value (LK Value).
The picture above also shows the standard deviations of the parameters. These are: [math]\displaystyle{ std(\sigma)\,\! }[/math] = 0.06, [math]\displaystyle{ std(\beta_{0})\,\! }[/math] = 1.5, [math]\displaystyle{ std(\beta_{1})\,\! }[/math] = 0.07. Therefore, their variances are: [math]\displaystyle{ Var(\sigma)\,\! }[/math] = 0.0036, [math]\displaystyle{ Var(\beta_{0})\,\! }[/math] = 2.25, [math]\displaystyle{ Var(\beta_{1})\,\! }[/math] = 0.0049. In terms of [math]\displaystyle{ \alpha_{1}\,\! }[/math] , the variance is [math]\displaystyle{ Var(\alpha_{1})\,\! }[/math] = 116052 and [math]\displaystyle{ Var(\beta_{1})\,\! }[/math] = 659912.5.
The difference of the variance in ALTA and the results in the book are caused by the precision in the book since results are provided only up to the 2nd decimal.
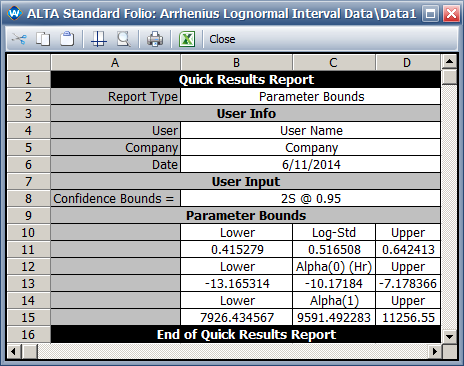
- The 95% two-sided confidence bounds on the parameters are shown next:
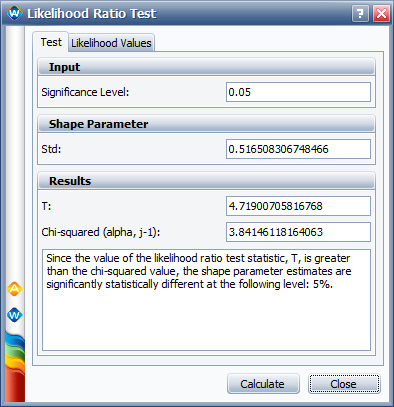
- The likelihood ratio common shape parameter test statistic is 4.7, as shown next.
As the results show, the values obtained by ALTA are very close to the results given in the book.
