Norris-Landzberg-Exponential Model: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Reference Example|ALTA_Reference_Examples_Banner.png|ALTA_Reference_Examples}} | {{Reference Example|ALTA_Reference_Examples_Banner.png|ALTA_Reference_Examples}} | ||
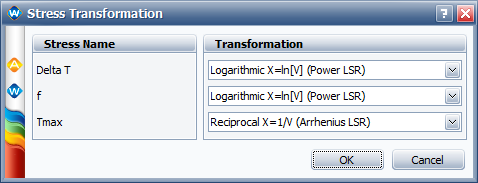
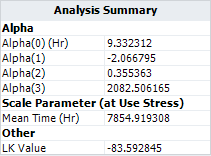
This example validates the calculation of the Norris-Landzberg relationship (can be done using the GLL model in ALTA with proper transformation for each stress). | |||
{{Reference_Example_Heading1}} | {{Reference_Example_Heading1}} | ||
The data set is from Example 7.2 on page 257 in book ''Life Cycle Reliability Engineering'' by Dr. Guangbin Yang, John Wiley & Sons, 2007. | |||
Revision as of 00:00, 10 June 2014
ALTA_Reference_Examples_Banner.png