Stress-Strength Interference: Difference between revisions
Jump to navigation
Jump to search
Kate Racaza (talk | contribs) Created page with '{{Reference Example}} This example compares the stress-strength interference results. {{Reference_Example_Heading1}} The data set is from Example 5.3 on page 129 in the book…' |
Kate Racaza (talk | contribs) No edit summary |
||
| Line 11: | Line 11: | ||
{{Reference_Example_Heading2}} | {{Reference_Example_Heading2}} | ||
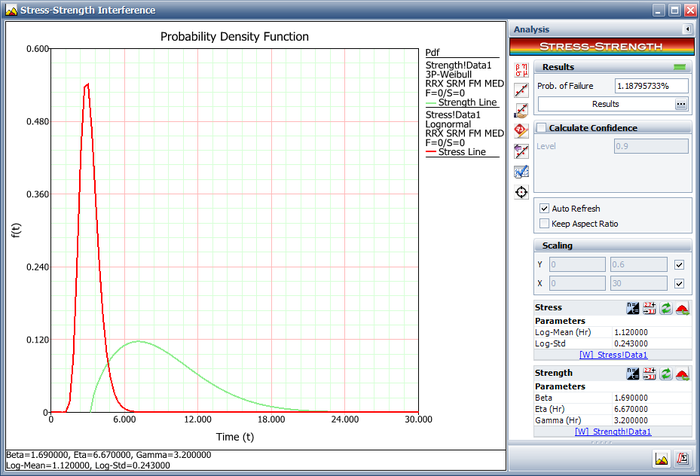
The stress (load) is a lognormal distribution with Ln-Mean = 1.12 and Ln-Std = 0.243. The strength is a | The stress (load) is a lognormal distribution with Ln-Mean = 1.12 and Ln-Std = 0.243. The strength is a 3-parameter Weibull distribution with Beta = 1.69, Eta = 6.67, and Gamma = 3.2. | ||
Revision as of 15:30, 13 June 2014
 |
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.