Crow-AMSAA Parameter Estimation Example: Difference between revisions
Chris Kahn (talk | contribs) No edit summary |
mNo edit summary |
||
| Line 59: | Line 59: | ||
For the failure terminated test, <math>{\beta}\,\!</math> is: | For the failure terminated test, <math>{\beta}\,\!</math> is: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 65: | Line 64: | ||
&=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} \\ | &=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} \\ | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
where: | where: | ||
:<math>\underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355\,\!</math> | :<math>\underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355\,\!</math> | ||
Then: | Then: | ||
:<math>\widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142\,\!</math> | :<math>\widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142\,\!</math> | ||
And for <math>{\lambda}\,\!</math> : | And for <math>{\lambda}\,\!</math> : | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 86: | Line 79: | ||
& =\frac{22}{{{620}^{0.6142}}}=0.4239 \\ | & =\frac{22}{{{620}^{0.6142}}}=0.4239 \\ | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
Therefore, <math>{{\lambda }_{i}}(T)\,\!</math> becomes: | Therefore, <math>{{\lambda }_{i}}(T)\,\!</math> becomes: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 95: | Line 86: | ||
= & 0.0217906\frac{\text{failures}}{\text{hr}} | = & 0.0217906\frac{\text{failures}}{\text{hr}} | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
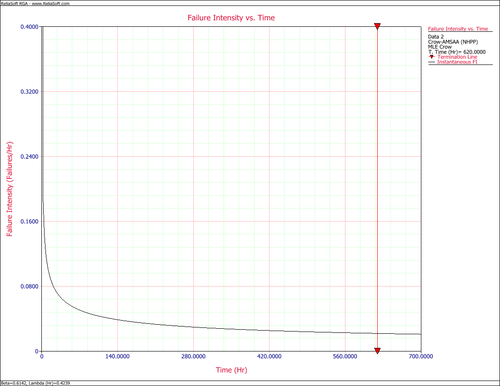
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is <math>\tfrac{1}{0.0217906}\,\!</math> or 46 hours. | The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is <math>\tfrac{1}{0.0217906}\,\!</math> or 46 hours. | ||
[[Image:FIvsTimeExample1.png|center|500px|Failure Intensity vs. Time plot]] | [[Image:FIvsTimeExample1.png|center|500px|Failure Intensity vs. Time plot]] | ||
Revision as of 20:49, 30 January 2014
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability Growth and Repairable System Analysis Reference book.
A prototype of a system was tested with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Row | Time to Event (hr) | [math]\displaystyle{ ln{(T)}\,\! }[/math] |
|---|---|---|
| 1 | 2.7 | 0.99325 |
| 2 | 10.3 | 2.33214 |
| 3 | 12.5 | 2.52573 |
| 4 | 30.6 | 3.42100 |
| 5 | 57.0 | 4.04305 |
| 6 | 61.3 | 4.11578 |
| 7 | 80.0 | 4.38203 |
| 8 | 109.5 | 4.69592 |
| 9 | 125.0 | 4.82831 |
| 10 | 128.6 | 4.85671 |
| 11 | 143.8 | 4.96842 |
| 12 | 167.9 | 5.12337 |
| 13 | 229.2 | 5.43459 |
| 14 | 296.7 | 5.69272 |
| 15 | 320.6 | 5.77019 |
| 16 | 328.2 | 5.79362 |
| 17 | 366.2 | 5.90318 |
| 18 | 396.7 | 5.98318 |
| 19 | 421.1 | 6.04287 |
| 20 | 438.2 | 6.08268 |
| 21 | 501.2 | 6.21701 |
| 22 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta}\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} \widehat{\beta }&=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} \\ &=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} \\ \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355\,\! }[/math]
Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142\,\! }[/math]
And for [math]\displaystyle{ {\lambda}\,\! }[/math] :
- [math]\displaystyle{ \begin{align} \widehat{\lambda }&=\frac{n}{{{T}^{*\beta }}} \\ & =\frac{22}{{{620}^{0.6142}}}=0.4239 \\ \end{align}\,\! }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T)\,\! }[/math] becomes:
- [math]\displaystyle{ \begin{align} {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align}\,\! }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906}\,\! }[/math] or 46 hours.