Gompertz Models: Difference between revisions
No edit summary |
|||
| Line 8: | Line 8: | ||
The Gompertz model is mathematically given by Virene [[RGA_References|[1]]]: | The Gompertz model is mathematically given by Virene [[RGA_References|[1]]]: | ||
::<math>R=a{{b}^{{{c}^{T}}}}</math> | ::<math>R=a{{b}^{{{c}^{T}}}}\,\!</math> | ||
where: | where: | ||
| Line 16: | Line 16: | ||
*<math>0<c<1\,\!</math> | *<math>0<c<1\,\!</math> | ||
*<math>T>0\,\!</math> | *<math>T>0\,\!</math> | ||
*<math>R=\,\!</math> | *<math>R=\,\!</math> the system's reliability at development time, launch number or stage number, <math>T\,\!</math>. | ||
*<math>a=\,\!</math> | *<math>a=\,\!</math> the upper limit that the reliability approaches asymptotically as <math>T\to \infty \,\!</math>, or the maximum reliability that can be attained. | ||
*<math>ab=\,\!</math> | *<math>ab=\,\!</math> initial reliability at <math>T=0.\,\!</math> | ||
*<math>c=\,\!</math> | *<math>c=\,\!</math> the growth pattern indicator (small values of <math>c\,\!</math> indicate rapid early reliability growth and large values of <math>c\,\!</math> indicate slow reliability growth). | ||
As it can be seen from the mathematical definition, the Gompertz model is a 3-parameter model with the parameters | As it can be seen from the mathematical definition, the Gompertz model is a 3-parameter model with the parameters <math>a\,\!</math>, <math>b\,\!</math> and <math>c\,\!</math>. The solution for the parameters, given <math>{{T}_{i}}\,\!</math> and <math>{{R}_{i}}\,\!</math>, is accomplished by fitting the best possible line through the data points. Many methods are available; all of which tend to be numerically intensive. When analyzing reliability data in the RGA software, you have the option to enter the reliability values in percent or in decimal format. However, <math>a\,\!</math> will always be returned in decimal format and not in percent. The estimated parameters in the RGA software are unitless. The next section presents an overview and background on some of the most commonly used algorithms/methods for obtaining these parameters. | ||
==Parameter Estimation== | ==Parameter Estimation== | ||
<PER LISA: ASK SME TO ADD SOME SORT OF INTRODUCTION THAT PREPARES THE READER FOR THE THREE SUBSECTIONS> | <PER LISA: ASK SME TO ADD SOME SORT OF INTRODUCTION THAT PREPARES THE READER FOR THE THREE SUBSECTIONS> | ||
===Linear Regression=== | ===Linear Regression=== | ||
The method of least squares requires that a straight line be fitted to a set of data points. If the regression is on | The method of least squares requires that a straight line be fitted to a set of data points. If the regression is on <math>Y\,\!</math>, then the sum of the squares of the vertical deviations from the points to the line is minimized. If the regression is on <math>X\,\!</math>, the line is fitted to a set of data points such that the sum of the squares of the horizontal deviations from the points to the line is minimized. To illustrate the method, this section presents a regression on <math>Y\,\!</math>. Consider the linear model given by Seber and Wild [[RGA_References|[2]]]: | ||
::<math>{{Y}_{i}}={{\widehat{\beta }}_{0}}+{{\widehat{\beta }}_{1}}{{X}_{i1}}+{{\widehat{\beta }}_{2}}{{X}_{i2}}+...+{{\widehat{\beta }}_{p}}{{X}_{ip}}</math> | ::<math>{{Y}_{i}}={{\widehat{\beta }}_{0}}+{{\widehat{\beta }}_{1}}{{X}_{i1}}+{{\widehat{\beta }}_{2}}{{X}_{i2}}+...+{{\widehat{\beta }}_{p}}{{X}_{ip}}\,\!</math> | ||
or in matrix form where bold letters indicate matrices: | or in matrix form where bold letters indicate matrices: | ||
| Line 34: | Line 34: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
Y=X\beta | Y=X\beta | ||
\end{align}</math> | \end{align}\,\!</math> | ||
:where: | :where: | ||
| Line 43: | Line 43: | ||
\vdots \\ | \vdots \\ | ||
{{Y}_{N}} \\ | {{Y}_{N}} \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
::<math>X=\left[ \begin{matrix} | ::<math>X=\left[ \begin{matrix} | ||
| Line 50: | Line 50: | ||
\vdots & \vdots & \ddots & \vdots \\ | \vdots & \vdots & \ddots & \vdots \\ | ||
1 & {{X}_{N,1}} & \cdots & {{X}_{N,p}} \\ | 1 & {{X}_{N,1}} & \cdots & {{X}_{N,p}} \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
<br> | <br> | ||
:and: | :and: | ||
| Line 59: | Line 59: | ||
\vdots \\ | \vdots \\ | ||
{{\beta }_{p}} \\ | {{\beta }_{p}} \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
The vector | The vector <math>\beta \,\!</math> holds the values of the parameters. Now let <math>\widehat{\beta }\,\!</math> be the estimates of these parameters, or the regression coefficients. The vector of estimated regression coefficients is denoted by: | ||
::<math>\widehat{\beta }=\left[ \begin{matrix} | ::<math>\widehat{\beta }=\left[ \begin{matrix} | ||
| Line 68: | Line 68: | ||
\vdots \\ | \vdots \\ | ||
{{\widehat{\beta }}_{p}} \\ | {{\widehat{\beta }}_{p}} \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
Solving for | Solving for <math>\beta \,\!</math> in Eqn. (linear) requires the analyst to left multiply both sides by the transpose of <math>X\,\!</math>, <math>{{X}^{T}}\,\!</math> : | ||
::<math>({{X}^{T}}X)\widehat{\beta }={{X}^{T}}Y</math> | ::<math>({{X}^{T}}X)\widehat{\beta }={{X}^{T}}Y\,\!</math> | ||
Now the term | Now the term <math>({{X}^{T}}X)\,\!</math> becomes a square and invertible matrix. Then taking it to the other side of the equation gives: | ||
::<math>\widehat{\beta }=({{X}^{T}}X)^{-1}{{X}^{T}}Y</math> | ::<math>\widehat{\beta }=({{X}^{T}}X)^{-1}{{X}^{T}}Y\,\!</math> | ||
===Nonlinear Regression=== | ===Nonlinear Regression=== | ||
Nonlinear regression is similar to linear regression, except that a curve is fitted to the data set instead of a straight line. Just as in the linear scenario, the sum of the squares of the horizontal and vertical distances between the line and the points are to be minimized. In the case of the nonlinear Gompertz model | Nonlinear regression is similar to linear regression, except that a curve is fitted to the data set instead of a straight line. Just as in the linear scenario, the sum of the squares of the horizontal and vertical distances between the line and the points are to be minimized. In the case of the nonlinear Gompertz model <math>R=a{{b}^{{{c}^{T}}}}\,\!</math>, let: | ||
::<math>{{Y}_{i}}=f({{T}_{i}},\delta )=a{{b}^{{{c}^{{{T}_{i}}}}}}</math> | ::<math>{{Y}_{i}}=f({{T}_{i}},\delta )=a{{b}^{{{c}^{{{T}_{i}}}}}}\,\!</math> | ||
:where: | :where: | ||
| Line 90: | Line 90: | ||
\vdots \\ | \vdots \\ | ||
{{T}_{N}} \\ | {{T}_{N}} \\ | ||
\end{matrix} \right],\quad i=1,2,...,N</math> | \end{matrix} \right],\quad i=1,2,...,N\,\!</math> | ||
:and: | :and: | ||
| Line 98: | Line 98: | ||
b \\ | b \\ | ||
c \\ | c \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
The Gauss-Newton method can be used to solve for the parameters | The Gauss-Newton method can be used to solve for the parameters <math>a\,\!</math>, <math>b\,\!</math> and <math>c\,\!</math> by performing a Taylor series expansion on <math>f({{T}_{i}},\delta ).\,\!</math> Then approximate the nonlinear model with linear terms and employ ordinary least squares to estimate the parameters. This procedure is performed in an iterative manner and it generally leads to a solution of the nonlinear problem. | ||
This procedure starts by using initial estimates of the parameters | This procedure starts by using initial estimates of the parameters <math>a\,\!</math>, <math>b\,\!</math> and <math>c\,\!</math>, denoted as <math>g_{1}^{(0)},\,\!</math> <math>g_{2}^{(0)}\,\!</math> and <math>g_{3}^{(0)},\,\!</math> where <math>^{(0)}\,\!</math> is the iteration number. The Taylor series expansion approximates the mean response, <math>f({{T}_{i}},\delta )\,\!</math>, around the starting values, <math>g_{1}^{(0)},\,\!</math> <math>g_{2}^{(0)}\,\!</math> and <math>g_{3}^{(0)}.\,\!</math> For the <math>{{i}^{th}}\,\!</math> observation: | ||
::<math>f({{T}_{i}},\delta )\simeq f({{T}_{i}},{{g}^{(0)}})+\underset{k=1}{\overset{p}{\mathop \sum }}\,{{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}}({{\delta }_{k}}-g_{k}^{(0)})</math> | ::<math>f({{T}_{i}},\delta )\simeq f({{T}_{i}},{{g}^{(0)}})+\underset{k=1}{\overset{p}{\mathop \sum }}\,{{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}}({{\delta }_{k}}-g_{k}^{(0)})\,\!</math> | ||
:where: | :where: | ||
| Line 112: | Line 112: | ||
g_{2}^{(0)} \\ | g_{2}^{(0)} \\ | ||
g_{3}^{(0)} \\ | g_{3}^{(0)} \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
:Let: | :Let: | ||
| Line 120: | Line 120: | ||
\nu _{k}^{(0)}= & ({{\delta }_{k}}-g_{k}^{(0)}) \\ | \nu _{k}^{(0)}= & ({{\delta }_{k}}-g_{k}^{(0)}) \\ | ||
D_{ik}^{(0)}= & {{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}} | D_{ik}^{(0)}= & {{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
So Eqn. (nl1) becomes: | So Eqn. (nl1) becomes: | ||
::<math>{{Y}_{i}}\simeq f_{i}^{(0)}+\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}</math> | ::<math>{{Y}_{i}}\simeq f_{i}^{(0)}+\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}\,\!</math> | ||
or by shifting | or by shifting <math>f_{i}^{(0)}\,\!</math> to the left of the equation: | ||
::<math>Y_{i}^{(0)}\simeq \underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}</math> | ::<math>Y_{i}^{(0)}\simeq \underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}\,\!</math> | ||
In matrix form this is given by: | In matrix form this is given by: | ||
::<math>{{Y}^{(0)}}\simeq {{D}^{(0)}}{{\nu }^{(0)}}</math> | ::<math>{{Y}^{(0)}}\simeq {{D}^{(0)}}{{\nu }^{(0)}}\,\!</math> | ||
:where: | :where: | ||
| Line 146: | Line 146: | ||
\vdots \\ | \vdots \\ | ||
{{Y}_{N}}-g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} \\ | {{Y}_{N}}-g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
:and: | :and: | ||
| Line 154: | Line 154: | ||
g_{2}^{(0)} \\ | g_{2}^{(0)} \\ | ||
g_{3}^{(0)} \\ | g_{3}^{(0)} \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
Note that Eqn. (matr) is in the form of the general linear regression model of Eqn. (linear). According to Eqn. (lincoeff), the estimate of the parameters | Note that Eqn. (matr) is in the form of the general linear regression model of Eqn. (linear). According to Eqn. (lincoeff), the estimate of the parameters <math>{{\nu }^{(0)}}\,\!</math> is given by: | ||
::<math>{{\widehat{\nu }}^{(0)}}={{\left( {{D}^{{{(0)}^{T}}}}{{D}^{(0)}} \right)}^{-1}}{{D}^{{{(0)}^{T}}}}{{Y}^{(0)}}</math> | ::<math>{{\widehat{\nu }}^{(0)}}={{\left( {{D}^{{{(0)}^{T}}}}{{D}^{(0)}} \right)}^{-1}}{{D}^{{{(0)}^{T}}}}{{Y}^{(0)}}\,\!</math> | ||
The revised estimated regression coefficients in matrix form are: | The revised estimated regression coefficients in matrix form are: | ||
::<math>{{g}^{(1)}}={{g}^{(0)}}+{{\widehat{\nu }}^{(0)}}</math> | ::<math>{{g}^{(1)}}={{g}^{(0)}}+{{\widehat{\nu }}^{(0)}}\,\!</math> | ||
The least squares criterion measure, | The least squares criterion measure, <math>Q,\,\!</math> should be checked to examine whether the revised regression coefficients will lead to a reasonable result. According to the Least Squares Principle, the solution to the values of the parameters are those values that minimize <math>Q\,\!</math>. With the starting coefficients, <math>{{g}^{(0)}}\,\!</math>, <math>Q\,\!</math> is: | ||
::<math>{{Q}^{(0)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(0)}} \right) \right]}^{2}}</math> | ::<math>{{Q}^{(0)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(0)}} \right) \right]}^{2}}\,\!</math> | ||
And with the coefficients at the end of the first iteration, | And with the coefficients at the end of the first iteration, <math>{{g}^{(1)}}\,\!</math>, <math>Q\,\!</math> is: | ||
::<math>{{Q}^{(1)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(1)}} \right) \right]}^{2}}</math> | ::<math>{{Q}^{(1)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(1)}} \right) \right]}^{2}}\,\!</math> | ||
For the Gauss-Newton method to work properly and to satisfy the Least Squares Principle, the relationship | For the Gauss-Newton method to work properly and to satisfy the Least Squares Principle, the relationship <math>{{Q}^{(k+1)}}<{{Q}^{(k)}}\,\!</math> has to hold for all <math>k\,\!</math>, meaning that <math>{{g}^{(k+1)}}\,\!</math> gives a better estimate than <math>{{g}^{(k)}}\,\!</math>. The problem is not yet completely solved. Now <math>{{g}^{(1)}}\,\!</math> are the starting values, producing a new set of values <math>{{g}^{(2)}}\,\!</math>. The process is continued until the following relationship has been satisfied: | ||
::<math>{{Q}^{(s-1)}}-{{Q}^{(s)}}\simeq 0</math> | ::<math>{{Q}^{(s-1)}}-{{Q}^{(s)}}\simeq 0\,\!</math> | ||
When using the Gauss-Newton method or some other estimation procedure, it is advisable to try several sets of starting values to make sure that the solution gives relatively consistent results. | When using the Gauss-Newton method or some other estimation procedure, it is advisable to try several sets of starting values to make sure that the solution gives relatively consistent results. | ||
| Line 183: | Line 183: | ||
Various methods were developed for obtaining valid initial values for the regression parameters. The following procedure is described by Virene [[RGA_References|[1]]] in estimating the Gompertz parameters. This procedure is rather simple. It will be used to get the starting values for the Gauss-Newton method, or for any other method that requires initial values. Some analysts are using this method to calculate the parameters if the data set is divisible into three groups of equal size. However, if the data set is not equally divisible, it can still provide good initial estimates. | Various methods were developed for obtaining valid initial values for the regression parameters. The following procedure is described by Virene [[RGA_References|[1]]] in estimating the Gompertz parameters. This procedure is rather simple. It will be used to get the starting values for the Gauss-Newton method, or for any other method that requires initial values. Some analysts are using this method to calculate the parameters if the data set is divisible into three groups of equal size. However, if the data set is not equally divisible, it can still provide good initial estimates. | ||
Consider the case where | Consider the case where <math>m\,\!</math> observations are available in the form shown next. Each reliability value, <math>{{R}_{i}}\,\!</math>, is measured at the specified times, <math>{{T}_{i}}\,\!</math>. | ||
::<math>\begin{matrix} | ::<math>\begin{matrix} | ||
| Line 192: | Line 192: | ||
\vdots & \vdots \\ | \vdots & \vdots \\ | ||
{{T}_{m-1}} & {{R}_{m-1}} \\ | {{T}_{m-1}} & {{R}_{m-1}} \\ | ||
\end{matrix}</math> | \end{matrix}\,\!</math> | ||
:where: | :where: | ||
:*<math>m=3n,\,\!</math> | :*<math>m=3n,\,\!</math> <math>n\,\!</math> is equal to the number of items in each equally sized group | ||
:*<math>{{T}_{i}}-{{T}_{i-1}}=const\,\!</math> | :*<math>{{T}_{i}}-{{T}_{i-1}}=const\,\!</math> | ||
:*<math>i=0,1,...,m-1\,\!</math> | :*<math>i=0,1,...,m-1\,\!</math> | ||
| Line 201: | Line 201: | ||
The Gompertz reliability equation is given by: | The Gompertz reliability equation is given by: | ||
::<math>R=a{{b}^{{{c}^{T}}}}</math> | ::<math>R=a{{b}^{{{c}^{T}}}}\,\!</math> | ||
:and: | :and: | ||
| Line 207: | Line 207: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
\ln (R)=\ln (a)+{{c}^{T}}\ln (b) | \ln (R)=\ln (a)+{{c}^{T}}\ln (b) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
:Define: | :Define: | ||
::<math>S_1=\sum_{i=0}^{n-1} ln(R_i)= n ln(a)+ln(b)\sum_{i=0}^{n-1} c^{T_i}</math> | ::<math>S_1=\sum_{i=0}^{n-1} ln(R_i)= n ln(a)+ln(b)\sum_{i=0}^{n-1} c^{T_i}\,\!</math> | ||
::<math>S_2=\sum_{i=n}^{2n-1} ln(R_i)= n ln(a)+ln(b)\sum_{i=n}^{2n-1} c^{T_i}</math> | ::<math>S_2=\sum_{i=n}^{2n-1} ln(R_i)= n ln(a)+ln(b)\sum_{i=n}^{2n-1} c^{T_i}\,\!</math> | ||
::<math>S_3=\sum_{i=2n}^{m-1} ln(R_i)= n ln(a)+ln(b)\sum_{i=2n}^{m-1} c^{T_i}</math> | ::<math>S_3=\sum_{i=2n}^{m-1} ln(R_i)= n ln(a)+ln(b)\sum_{i=2n}^{m-1} c^{T_i}\,\!</math> | ||
:Then: | :Then: | ||
::<math>\frac{S_3-S_2}{S_2-S_1}=\frac{\sum_{i=2n}{m-1} c^{T_i}-\sum_{i=n}^{2n-1} c^T_i}{\sum_{i=0}^{n-1} c^{T_i}}</math> | ::<math>\frac{S_3-S_2}{S_2-S_1}=\frac{\sum_{i=2n}{m-1} c^{T_i}-\sum_{i=n}^{2n-1} c^T_i}{\sum_{i=0}^{n-1} c^{T_i}}\,\!</math> | ||
::<math>\frac{S_3-S_2}{S_2-S_1}=c^T_{2n}\frac{\sum_{i=0}{n-1} c^{T_i}-c^{T_n}\sum_{i=0}^{n-1} c^T_i}{c^{T_n}\sum_{i=0}^{n-1} c^{T_i}}</math> | ::<math>\frac{S_3-S_2}{S_2-S_1}=c^T_{2n}\frac{\sum_{i=0}{n-1} c^{T_i}-c^{T_n}\sum_{i=0}^{n-1} c^T_i}{c^{T_n}\sum_{i=0}^{n-1} c^{T_i}}\,\!</math> | ||
::<math>\frac{S_3 - S_2}{S_2-S_1}=\frac{c^{T_2n}-c^{T_n}}{c^{T_n}-1}=c^{T_{a_n}}=c^{n\cdot I+T_0}</math> | ::<math>\frac{S_3 - S_2}{S_2-S_1}=\frac{c^{T_2n}-c^{T_n}}{c^{T_n}-1}=c^{T_{a_n}}=c^{n\cdot I+T_0}\,\!</math> | ||
Without loss of generality, take | Without loss of generality, take <math>{{T}_{{{a}_{0}}}}=0\,\!</math> ; then: | ||
::<math>\frac{{{S}_{3}}-{{S}_{2}}}{{{S}_{2}}-{{S}_{1}}}={{c}^{n\cdot I}}</math> | ::<math>\frac{{{S}_{3}}-{{S}_{2}}}{{{S}_{2}}-{{S}_{1}}}={{c}^{n\cdot I}}\,\!</math> | ||
Solving for | Solving for <math>c\,\!</math> yields: | ||
<<NEED TO ADD AN EQUATION>> | <<NEED TO ADD AN EQUATION>> | ||
| Line 232: | Line 232: | ||
{{S}_{1}}-n\cdot \ln (a)= & \ln (b)\underset{i=0}{\overset{n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \\ | {{S}_{1}}-n\cdot \ln (a)= & \ln (b)\underset{i=0}{\overset{n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \\ | ||
{{S}_{2}}-n\cdot \ln (a)= & \ln (b)\underset{i=n}{\overset{2n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} | {{S}_{2}}-n\cdot \ln (a)= & \ln (b)\underset{i=n}{\overset{2n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
:or: | :or: | ||
::<math>\frac{{{S}_{1}}-n\cdot \ln (a)}{{{S}_{2}}-n\cdot \ln (a)}=\frac{1}{{{c}^{n\cdot I}}}</math> | ::<math>\frac{{{S}_{1}}-n\cdot \ln (a)}{{{S}_{2}}-n\cdot \ln (a)}=\frac{1}{{{c}^{n\cdot I}}}\,\!</math> | ||
Reordering the equation yields: | Reordering the equation yields: | ||
| Line 243: | Line 243: | ||
\ln (a)= & \frac{1}{n}\left( {{S}_{1}}+\frac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n\cdot I}}} \right) \\ | \ln (a)= & \frac{1}{n}\left( {{S}_{1}}+\frac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n\cdot I}}} \right) \\ | ||
a= & {{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}+\tfrac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n\cdot I}}} \right) \right]}} | a= & {{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}+\tfrac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n\cdot I}}} \right) \right]}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
If the reliability values are in percent then | If the reliability values are in percent then <math>a\,\!</math> needs to be divided by 100 to return the estimate in decimal format. Consider Eqns. (gomp3a) and (gomp3b) again, where: | ||
<<NEED TO ADD AN EQUATION>> | <<NEED TO ADD AN EQUATION>> | ||
| Line 254: | Line 254: | ||
\ln (b)= & \frac{({{S}_{2}}-{{S}_{1}})({{c}^{I}}-1)}{{{(1-{{c}^{n\cdot I}})}^{2}}} \\ | \ln (b)= & \frac{({{S}_{2}}-{{S}_{1}})({{c}^{I}}-1)}{{{(1-{{c}^{n\cdot I}})}^{2}}} \\ | ||
b= & {{e}^{\left[ \tfrac{\left( {{S}_{2}}-{{S}_{1}} \right)\left( {{c}^{I}}-1 \right)}{{{\left( 1-{{c}^{n\cdot I}} \right)}^{2}}} \right]}} | b= & {{e}^{\left[ \tfrac{\left( {{S}_{2}}-{{S}_{1}} \right)\left( {{c}^{I}}-1 \right)}{{{\left( 1-{{c}^{n\cdot I}} \right)}^{2}}} \right]}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
For the special case where | For the special case where <math>I=1\,\!</math>, from Eqns. (gomp4), (gomp5) and (gomp7), the parameters are: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 262: | Line 262: | ||
a= & {{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}+\tfrac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n}}} \right) \right]}} \\ | a= & {{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}+\tfrac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n}}} \right) \right]}} \\ | ||
b= & {{e}^{\left[ \tfrac{({{S}_{2}}-{{S}_{1}})(c-1)}{{{\left( 1-{{c}^{n}} \right)}^{2}}} \right]}} | b= & {{e}^{\left[ \tfrac{({{S}_{2}}-{{S}_{1}})(c-1)}{{{\left( 1-{{c}^{n}} \right)}^{2}}} \right]}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
To estimate the values of the parameters | To estimate the values of the parameters <math>a,b\,\!</math> and <math>c\,\!</math>, do the following: | ||
:1) Arrange the currently available data in terms of | :1) Arrange the currently available data in terms of <math>T\,\!</math> and <math>R\,\!</math> as in the table below. The <math>T\,\!</math> values should be chosen at equal intervals and increasing in value by 1, such as one month, one hour, etc. | ||
{|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | ||
| Line 279: | Line 279: | ||
|1|| 1|| 66|| 4.190 | |1|| 1|| 66|| 4.190 | ||
|- | |- | ||
| || || || <math>{{S}_{1}}</math> | | || || || <math>{{S}_{1}}\,\!</math> = 8.250 | ||
|- | |- | ||
| || 2|| 72.5|| 4.284 | | || 2|| 72.5|| 4.284 | ||
| Line 285: | Line 285: | ||
|2|| 3|| 78|| 4.357 | |2|| 3|| 78|| 4.357 | ||
|- | |- | ||
| || || || <math>{{S}_{2}}</math> | | || || || <math>{{S}_{2}}\,\!</math> = 8.641 | ||
|- | |- | ||
| || 4|| 82|| 4.407 | | || 4|| 82|| 4.407 | ||
| Line 291: | Line 291: | ||
|3|| 5|| 85|| 4.443 | |3|| 5|| 85|| 4.443 | ||
|- | |- | ||
| || || || <math>{{S}_{3}}</math> | | || || || <math>{{S}_{3}}\,\!</math> = 8.850 | ||
|} | |} | ||
:2) Calculate the natural log | :2) Calculate the natural log <math>R\,\!</math>. | ||
:3) Divide the column of values for log | :3) Divide the column of values for log <math>R\,\!</math> into three groups of equal size, each containing <math>n\,\!</math> items. There should always be three groups. Each group should always have the same number, <math>n\,\!</math>, of items, measurements or values. | ||
:4) Add the values of the natural log | :4) Add the values of the natural log <math>R\,\!</math> in each group, obtaining the sums identified as <math>{{S}_{1}}\,\!</math>, <math>{{S}_{2}}\,\!</math> and <math>{{S}_{3}}\,\!</math>, starting with the lowest values of the natural log <math>R\,\!</math>. | ||
:5) Calculate | :5) Calculate <math>c\,\!</math> from Eqn. (eq9): | ||
::<math>c={{\left( \frac{{{S}_{3}}-{{S}_{2}}}{{{S}_{2}}-{{S}_{1}}} \right)}^{\tfrac{1}{n}}}</math> | ::<math>c={{\left( \frac{{{S}_{3}}-{{S}_{2}}}{{{S}_{2}}-{{S}_{1}}} \right)}^{\tfrac{1}{n}}}\,\!</math> | ||
:6) Calculate | :6) Calculate <math>a\,\!</math> from Eqn. (eq10): | ||
::<math>a={{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}+\tfrac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n}}} \right) \right]}}</math> | ::<math>a={{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}+\tfrac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n}}} \right) \right]}}\,\!</math> | ||
:7) Calculate | :7) Calculate <math>b\,\!</math> from Eqn. (eq11): | ||
::<math>b={{e}^{\left[ \tfrac{({{S}_{2}}-{{S}_{1}})(c-1)}{{{\left( 1-{{c}^{n}} \right)}^{2}}} \right]}}</math> | ::<math>b={{e}^{\left[ \tfrac{({{S}_{2}}-{{S}_{1}})(c-1)}{{{\left( 1-{{c}^{n}} \right)}^{2}}} \right]}}\,\!</math> | ||
:8) Write the Gompertz reliability growth equation. | :8) Write the Gompertz reliability growth equation. | ||
:9) Substitute the value of | :9) Substitute the value of <math>T\,\!</math>, the time at which the reliability goal is to be achieved, to see if the reliability is indeed to be attained or exceeded by <math>T\,\!</math>. | ||
==Confidence Bounds== | ==Confidence Bounds== | ||
The approximate reliability confidence bounds under the Gompertz model can be obtained with nonlinear regression. Additionally, the reliability is always between 0 and 1. In order to keep the endpoints of the confidence interval, the logit transformation is used to obtain the confidence bounds on reliability. | The approximate reliability confidence bounds under the Gompertz model can be obtained with nonlinear regression. Additionally, the reliability is always between 0 and 1. In order to keep the endpoints of the confidence interval, the logit transformation is used to obtain the confidence bounds on reliability. | ||
::<math>CB=\frac{{{{\hat{R}}}_{i}}}{{{{\hat{R}}}_{i}}+(1-{{{\hat{R}}}_{i}}){{e}^{\pm {{z}_{\alpha }}{{{\hat{\sigma }}}_{R}}/\left[ {{{\hat{R}}}_{i}}(1-{{{\hat{R}}}_{i}}) \right]}}}</math> | ::<math>CB=\frac{{{{\hat{R}}}_{i}}}{{{{\hat{R}}}_{i}}+(1-{{{\hat{R}}}_{i}}){{e}^{\pm {{z}_{\alpha }}{{{\hat{\sigma }}}_{R}}/\left[ {{{\hat{R}}}_{i}}(1-{{{\hat{R}}}_{i}}) \right]}}}\,\!</math> | ||
::<math>{{\hat{\sigma }}^{2}}=\frac{SSE}{n-p}</math> | ::<math>{{\hat{\sigma }}^{2}}=\frac{SSE}{n-p}\,\!</math> | ||
where | where <math>p\,\!</math> is the total number of groups (in this case 3) and <math>n\,\!</math> is the total number of items in each group. | ||
==Example: Standard Gompertz for Reliability Data== | ==Example: Standard Gompertz for Reliability Data== | ||
| Line 335: | Line 335: | ||
|1|| 1|| 66|| 4.190 | |1|| 1|| 66|| 4.190 | ||
|- | |- | ||
| || || || <math>{{S}_{1}}</math> | | || || || <math>{{S}_{1}}\,\!</math> = 8.250 | ||
|- | |- | ||
| || 2|| 72.5|| 4.284 | | || 2|| 72.5|| 4.284 | ||
| Line 341: | Line 341: | ||
|2|| 3|| 78|| 4.357 | |2|| 3|| 78|| 4.357 | ||
|- | |- | ||
| || || || <math>{{S}_{2}}</math> | | || || || <math>{{S}_{2}}\,\!</math> = 8.641 | ||
|- | |- | ||
| || 4|| 82|| 4.407 | | || 4|| 82|| 4.407 | ||
| Line 347: | Line 347: | ||
|3|| 5|| 85|| 4.443 | |3|| 5|| 85|| 4.443 | ||
|- | |- | ||
| || || || <math>{{S}_{3}}</math> | | || || || <math>{{S}_{3}}\,\!</math> = 8.850 | ||
|} | |} | ||
'''Solution''' | '''Solution''' | ||
Having completed Steps 1 through 4 by preparing the table and calculating the last column to find | Having completed Steps 1 through 4 by preparing the table and calculating the last column to find <math>{{S}_{1}}\,\!</math>, <math>{{S}_{2}}\,\!</math> and <math>{{S}_{3}}\,\!</math>, proceed as follows: | ||
:a) Find | :a) Find <math>c\,\!</math> from Eqn. (eq9). | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
c= & {{\left( \frac{8.850-8.641}{8.641-8.250} \right)}^{\tfrac{1}{2}}} \\ | c= & {{\left( \frac{8.850-8.641}{8.641-8.250} \right)}^{\tfrac{1}{2}}} \\ | ||
= & 0.731 | = & 0.731 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
:b) Find | :b) Find <math>a\,\!</math> from Eqn. (eq10). | ||
::This is the upper limit for the reliability as | ::This is the upper limit for the reliability as <math>T\to \infty \,\!</math>. | ||
:c) Find | :c) Find <math>b\,\!</math> from Eqn. (eq11). | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 371: | Line 371: | ||
= & {{e}^{(-0.485)}} \\ | = & {{e}^{(-0.485)}} \\ | ||
= & 0.615 | = & 0.615 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::Now, since the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting | ::Now, since the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting <math>{{Y}_{i}}={{R}_{i}},\,\!</math> <math>g_{1}^{(0)}=94.16,\,\!</math> <math>g_{2}^{(0)}=0.615,\,\!</math> <math>g_{3}^{(0)}=0.731,\,\!</math> <math>{{Y}^{(0)}},{{D}^{(0)}},\,\!</math> <math>{{\nu }^{(0)}}\,\!</math> become: | ||
::<math>{{Y}^{(0)}}=\left[ \begin{matrix} | ::<math>{{Y}^{(0)}}=\left[ \begin{matrix} | ||
| Line 382: | Line 382: | ||
0.0439 \\ | 0.0439 \\ | ||
-0.0743 \\ | -0.0743 \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
::<math>{{D}^{(0)}}=\left[ \begin{matrix} | ::<math>{{D}^{(0)}}=\left[ \begin{matrix} | ||
0.6150 & 94.1600 & 0.0000 \\ | 0.6150 & 94.1600 & 0.0000 \\ | ||
| Line 390: | Line 390: | ||
0.8704 & 38.0519 & -62.2513 \\ | 0.8704 & 38.0519 & -62.2513 \\ | ||
0.9035 & 28.8742 & -59.0463 \\ | 0.9035 & 28.8742 & -59.0463 \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
::<math>{{\nu }^{(0)}}=\left[ \begin{matrix} | ::<math>{{\nu }^{(0)}}=\left[ \begin{matrix} | ||
g_{1}^{(0)} \\ | g_{1}^{(0)} \\ | ||
| Line 399: | Line 399: | ||
0.615 \\ | 0.615 \\ | ||
0.731 \\ | 0.731 \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
The estimate of the parameters | The estimate of the parameters <math>{{\nu }^{(0)}}\,\!</math> is given by: | ||
The revised estimated regression coefficients in matrix form are: | The revised estimated regression coefficients in matrix form are: | ||
| Line 407: | Line 407: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
{{Q}^{(k+1)}}<{{Q}^{(k)}} | {{Q}^{(k+1)}}<{{Q}^{(k)}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
If the Gauss-Newton method works effectively, then the relationship has to hold, meaning that | If the Gauss-Newton method works effectively, then the relationship has to hold, meaning that <math>{{g}^{(k+1)}}\,\!</math> gives better estimates than <math>{{g}^{(k)}}\,\!</math>, after <math>k\,\!</math>. With the starting coefficients, <math>{{g}^{(0)}},\,\!</math> <math>Q\,\!</math> is: | ||
And with the coefficients at the end of the first iteration, | And with the coefficients at the end of the first iteration, <math>{{g}^{(1)}},\,\!</math> <math>Q\,\!</math> is: | ||
Therefore, it can be justified that the Gauss-Newton method works in the right direction. The iterations are continued until the relationship of Eqn.(crit) is satisfied. Note that the RGA siftware uses a different analysis method called the Levenberg-Marquardt. This method utilizes the best features of the Gauss-Newton method and the method of the steepest descent, and occupies a middle ground between these two methods. The estimated parameters using RGA are shown in the figure below. | Therefore, it can be justified that the Gauss-Newton method works in the right direction. The iterations are continued until the relationship of Eqn.(crit) is satisfied. Note that the RGA siftware uses a different analysis method called the Levenberg-Marquardt. This method utilizes the best features of the Gauss-Newton method and the method of the steepest descent, and occupies a middle ground between these two methods. The estimated parameters using RGA are shown in the figure below. | ||
| Line 423: | Line 423: | ||
& \widehat{b}= & 0.6152 \\ | & \widehat{b}= & 0.6152 \\ | ||
& \widehat{c}= & 0.7321 | & \widehat{c}= & 0.7321 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
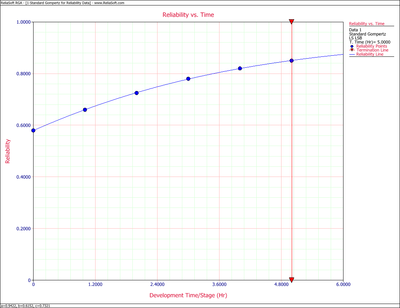
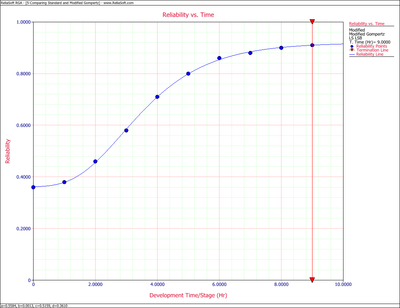
The Gompertz reliability growth curve is: | The Gompertz reliability growth curve is: | ||
::<math>R=0.9422{{(0.6152)}^{{{0.7321}^{T}}}}</math> | ::<math>R=0.9422{{(0.6152)}^{{{0.7321}^{T}}}}\,\!</math> | ||
:1) The achievable reliability at the end of the 12-month period of design and development is: | :1) The achievable reliability at the end of the 12-month period of design and development is: | ||
| Line 433: | Line 433: | ||
The required reliability is 92%. Consequently, from the previous result, this requirement will barely be met. Every effort should therefore be expended to implement the reliability program plan fully, and perhaps augment it slightly to assure that the reliability goal will be met. | The required reliability is 92%. Consequently, from the previous result, this requirement will barely be met. Every effort should therefore be expended to implement the reliability program plan fully, and perhaps augment it slightly to assure that the reliability goal will be met. | ||
:2) The maximum achievable reliability from Step 2, or from the value of | :2) The maximum achievable reliability from Step 2, or from the value of <math>a\,\!</math>, is 0.9422. | ||
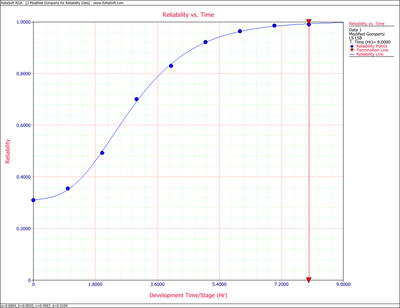
:3) The predicted reliability values, as calculated from the Gompertz equation, Eqn. (eq8), are compared with the actual data in the table below. It may be seen in the table that the Gompertz curve appears to provide a very good fit for the data used because the equation reproduces the available data with less than 1% error. Eqn. (eq8) is plotted in the figure below the table and identifies the type of reliability growth curve this equation represents. | :3) The predicted reliability values, as calculated from the Gompertz equation, Eqn. (eq8), are compared with the actual data in the table below. It may be seen in the table that the Gompertz curve appears to provide a very good fit for the data used because the equation reproduces the available data with less than 1% error. Eqn. (eq8) is plotted in the figure below the table and identifies the type of reliability growth curve this equation represents. | ||
| Line 543: | Line 543: | ||
For many kinds of equipment, especially missiles and space systems, only success/failure data (also called discrete or attribute data) is obtained. Conservatively, the cumulative reliability can be used to estimate the trend of reliability growth. The cumulative reliability is given by Kececioglu [[RGA_References|[3]]]: | For many kinds of equipment, especially missiles and space systems, only success/failure data (also called discrete or attribute data) is obtained. Conservatively, the cumulative reliability can be used to estimate the trend of reliability growth. The cumulative reliability is given by Kececioglu [[RGA_References|[3]]]: | ||
::<math>\bar{R}(N)=\frac{N-r}{N}</math> | ::<math>\bar{R}(N)=\frac{N-r}{N}\,\!</math> | ||
where: | where: | ||
| Line 557: | Line 557: | ||
If we apply a shift in the vertical coordinate, then the Gompertz model is defined by: | If we apply a shift in the vertical coordinate, then the Gompertz model is defined by: | ||
::<math>R=d+a{{b}^{{{c}^{T}}}}</math> | ::<math>R=d+a{{b}^{{{c}^{T}}}}\,\!</math> | ||
where: | where: | ||
| Line 573: | Line 573: | ||
==Parameter Estimation== | ==Parameter Estimation== | ||
To implement the Modified Gompertz growth model, initial values of the parameters | To implement the Modified Gompertz growth model, initial values of the parameters <math>a\,\!</math>, <math>b\,\!</math>, <math>c\,\!</math> and <math>d\,\!</math> must be determined. When analyzing reliability data in RGA, you have the option to enter the reliability values in percent or in decimal format. However, <math>a\,\!</math> and <math>d\,\!</math> will always be returned in decimal format and not in percent. The estimated parameters in RGA are unitless. | ||
Given that | Given that <math>R=d+a{{b}^{{{c}^{T}}}}\,\!</math> and <math>\ln (R-d)=\ln (a)+{{c}^{T}}\ln (b)\,\!</math>, it follows that <math>{{S}_{1}}\,\!</math>, <math>{{S}_{2}}\,\!</math> and <math>{{S}_{3}}\,\!</math>, as defined in the derivation of the Standard Gompertz model, can be expressed as functions of <math>d\,\!</math>. | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 581: | Line 581: | ||
{{S}_{2}}(d)= & \underset{i=n}{\overset{2n-1}{\mathop \sum }}\,\ln ({{R}_{i}}-d)=n\ln (a)+\ln (b)\underset{i=n}{\overset{2n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \\ | {{S}_{2}}(d)= & \underset{i=n}{\overset{2n-1}{\mathop \sum }}\,\ln ({{R}_{i}}-d)=n\ln (a)+\ln (b)\underset{i=n}{\overset{2n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \\ | ||
{{S}_{3}}(d)= & \underset{i=2n}{\overset{m-1}{\mathop \sum }}\,\ln ({{R}_{i}}-d)=n\ln (a)+\ln (b)\underset{i=2n}{\overset{m-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} | {{S}_{3}}(d)= & \underset{i=2n}{\overset{m-1}{\mathop \sum }}\,\ln ({{R}_{i}}-d)=n\ln (a)+\ln (b)\underset{i=2n}{\overset{m-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
Modifying the equations given above in the [[Gompertz_Models#Choice_of_Initial_Values|Standard Gompertz Parameter Estimation section]] as functions of | Modifying the equations given above in the [[Gompertz_Models#Choice_of_Initial_Values|Standard Gompertz Parameter Estimation section]] as functions of <math>d\,\!</math> yields: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 589: | Line 589: | ||
a(d)= & {{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}(d)+\tfrac{{{S}_{2}}(d)-{{S}_{1}}(d)}{1-{{[c(d)]}^{n\cdot I}}} \right) \right]}} \\ | a(d)= & {{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}(d)+\tfrac{{{S}_{2}}(d)-{{S}_{1}}(d)}{1-{{[c(d)]}^{n\cdot I}}} \right) \right]}} \\ | ||
b(d)= & {{e}^{\left[ \tfrac{\left[ {{S}_{2}}(d)-{{S}_{1}}(d) \right]\left[ {{[c(d)]}^{I}}-1 \right]}{{{\left[ 1-{{[c(d)]}^{n\cdot I}} \right]}^{2}}} \right]}} | b(d)= & {{e}^{\left[ \tfrac{\left[ {{S}_{2}}(d)-{{S}_{1}}(d) \right]\left[ {{[c(d)]}^{I}}-1 \right]}{{{\left[ 1-{{[c(d)]}^{n\cdot I}} \right]}^{2}}} \right]}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where | where <math>I\,\!</math> is the time interval increment. At this point, you can use the initial constraint of: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
d+ab=\text{original level of reliability at }T=0 | d+ab=\text{original level of reliability at }T=0 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
Now there are four equations, Eqns. (eq17), (eq18), (eq19) and (eq20), and four unknowns, | Now there are four equations, Eqns. (eq17), (eq18), (eq19) and (eq20), and four unknowns, <math>a\,\!</math>, <math>b\,\!</math>, <math>c\,\!</math> and <math>d\,\!</math>. The simultaneous solution of these equations yields the four initial values for the parameters of the Modified Gompertz model. This procedure is similar to the one discussed before. It starts by using initial estimates of the parameters, <math>a\,\!</math>, <math>b\,\!</math>, <math>c\,\!</math> and <math>d\,\!</math>, denoted as <math>g_{1}^{(0)},\,\!</math> <math>g_{2}^{(0)},\,\!</math> <math>g_{3}^{(0)},\,\!</math> and <math>g_{4}^{(0)},\,\!</math> where <math>^{(0)}\,\!</math> is the iteration number. | ||
The Taylor series expansion approximates the mean response, | The Taylor series expansion approximates the mean response, <math>f({{T}_{i}},\delta )\,\!</math>, around the starting values, <math>g_{1}^{(0)},\,\!</math> <math>g_{2}^{(0)},\,\!</math> <math>g_{3}^{(0)}\,\!</math> and <math>g_{4}^{(0)}\,\!</math>. For the <math>{{i}^{th}}\,\!</math> observation: | ||
::<math>f({{T}_{i}},\delta )\simeq f({{T}_{i}},{{g}^{(0)}})+\underset{k=1}{\overset{p}{\mathop \sum }}\,{{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}}\cdot ({{\delta }_{k}}-g_{k}^{(0)})</math> | ::<math>f({{T}_{i}},\delta )\simeq f({{T}_{i}},{{g}^{(0)}})+\underset{k=1}{\overset{p}{\mathop \sum }}\,{{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}}\cdot ({{\delta }_{k}}-g_{k}^{(0)})\,\!</math> | ||
:where: | :where: | ||
| Line 610: | Line 610: | ||
g_{3}^{(0)} \\ | g_{3}^{(0)} \\ | ||
g_{4}^{(0)} \\ | g_{4}^{(0)} \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
:Let: | :Let: | ||
| Line 618: | Line 618: | ||
\nu _{k}^{(0)}= & ({{\delta }_{k}}-g_{k}^{(0)}) \\ | \nu _{k}^{(0)}= & ({{\delta }_{k}}-g_{k}^{(0)}) \\ | ||
D_{ik}^{(0)}= & {{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}} | D_{ik}^{(0)}= & {{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
:Therefore: | :Therefore: | ||
::<math>{{Y}_{i}}=f_{i}^{(0)}+\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}</math> | ::<math>{{Y}_{i}}=f_{i}^{(0)}+\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}\,\!</math> | ||
or by shifting | or by shifting <math>f_{i}^{(0)}\,\!</math> to the left of the equation: | ||
::<math>Y_{i}^{(0)}-f_{i}^{(0)}=\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}</math> | ::<math>Y_{i}^{(0)}-f_{i}^{(0)}=\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}\,\!</math> | ||
In matrix form, this is given by: | In matrix form, this is given by: | ||
::<math>{{Y}^{(0)}}\simeq {{D}^{(0)}}{{\nu }^{(0)}}</math> | ::<math>{{Y}^{(0)}}\simeq {{D}^{(0)}}{{\nu }^{(0)}}\,\!</math> | ||
where: | where: | ||
| Line 644: | Line 644: | ||
. \\ | . \\ | ||
{{Y}_{N}}-g_{4}^{(0)}+g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} \\ | {{Y}_{N}}-g_{4}^{(0)}+g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 659: | Line 659: | ||
g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & \tfrac{g_{1}^{(0)}}{g_{2}^{(0)}}g_{3}^{(0){{T}_{N}}}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & \tfrac{g_{1}^{(0)}}{g_{3}^{(0)}}g_{3}^{(0){{T}_{N}}}\ln (g_{2}^{(0)}){{T}_{N}}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & 1 \\ | g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & \tfrac{g_{1}^{(0)}}{g_{2}^{(0)}}g_{3}^{(0){{T}_{N}}}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & \tfrac{g_{1}^{(0)}}{g_{3}^{(0)}}g_{3}^{(0){{T}_{N}}}\ln (g_{2}^{(0)}){{T}_{N}}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & 1 \\ | ||
\end{matrix} \right] | \end{matrix} \right] | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::<math>{{\nu }^{(0)}}=\left[ \begin{matrix} | ::<math>{{\nu }^{(0)}}=\left[ \begin{matrix} | ||
| Line 666: | Line 666: | ||
g_{3}^{(0)} \\ | g_{3}^{(0)} \\ | ||
g_{4}^{(0)} \\ | g_{4}^{(0)} \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
The same reasoning as before is followed here, and the estimate of the parameters | The same reasoning as before is followed here, and the estimate of the parameters <math>{{\nu }^{(0)}}\,\!</math> is given by: | ||
::<math>{{\widehat{\nu }}^{(0)}}={{\left( {{D}^{{{(0)}^{T}}}}{{D}^{(0)}} \right)}^{-1}}{{D}^{{{(0)}^{T}}}}{{Y}^{(0)}}</math> | ::<math>{{\widehat{\nu }}^{(0)}}={{\left( {{D}^{{{(0)}^{T}}}}{{D}^{(0)}} \right)}^{-1}}{{D}^{{{(0)}^{T}}}}{{Y}^{(0)}}\,\!</math> | ||
The revised estimated regression coefficients in matrix form are: | The revised estimated regression coefficients in matrix form are: | ||
::<math>{{g}^{(1)}}={{g}^{(0)}}+{{\widehat{\nu }}^{(0)}}</math> | ::<math>{{g}^{(1)}}={{g}^{(0)}}+{{\widehat{\nu }}^{(0)}}\,\!</math> | ||
To see if the revised regression coefficients will lead to a reasonable result, the least squares criterion measure, , should be checked. According to the Least Squares Principle, the solution to the values of the parameters are those values that minimize | To see if the revised regression coefficients will lead to a reasonable result, the least squares criterion measure, , should be checked. According to the Least Squares Principle, the solution to the values of the parameters are those values that minimize <math>Q\,\!</math>. With the starting coefficients, <math>{{g}^{(0)}}\,\!</math>, <math>Q\,\!</math> is: | ||
::<math>{{Q}^{(0)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(0)}}) \right)}^{2}}</math> | ::<math>{{Q}^{(0)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(0)}}) \right)}^{2}}\,\!</math> | ||
With the coefficients at the end of the first iteration, | With the coefficients at the end of the first iteration, <math>{{g}^{(1)}}\,\!</math>, <math>Q\,\!</math> is: | ||
::<math>{{Q}^{(1)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(1)}}) \right)}^{2}}</math> | ::<math>{{Q}^{(1)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(1)}}) \right)}^{2}}\,\!</math> | ||
For the Gauss-Newton method to work properly, and to satisfy the Least Squares Principle, the relationship | For the Gauss-Newton method to work properly, and to satisfy the Least Squares Principle, the relationship <math>{{Q}^{(k+1)}}<{{Q}^{(k)}}\,\!</math> has to hold for all <math>k\,\!</math>, meaning that <math>{{g}^{(k+1)}}\,\!</math> gives a better estimate than <math>{{g}^{(k)}}\,\!</math>. The problem is not yet completely solved. Now <math>{{g}^{(1)}}\,\!</math> are the starting values, producing a new set of values <math>{{g}^{(2)}}.\,\!</math> The process is continued until the following relationship has been satisfied. | ||
::<math>{{Q}^{(s-1)}}-{{Q}^{(s)}}\simeq 0</math> | ::<math>{{Q}^{(s-1)}}-{{Q}^{(s)}}\simeq 0\,\!</math> | ||
As mentioned previously, when using the Gauss-Newton method or some other estimation procedure, it is advisable to try several sets of starting values to make sure that the solution gives relatively consistent results. Note that RGA uses a different analysis method called the Levenberg-Marquardt. This method utilizes the best features of the Gauss-Newton method and the method of the steepest descent, and occupies a middle ground between these two methods. | As mentioned previously, when using the Gauss-Newton method or some other estimation procedure, it is advisable to try several sets of starting values to make sure that the solution gives relatively consistent results. Note that RGA uses a different analysis method called the Levenberg-Marquardt. This method utilizes the best features of the Gauss-Newton method and the method of the steepest descent, and occupies a middle ground between these two methods. | ||
| Line 694: | Line 694: | ||
The approximate reliability confidence bounds under the Modified Gompertz model can be obtained using nonlinear regression. Additionally, the reliability is always between 0 and 1. In order to keep the endpoints of the confidence interval, the logit transformation can be used to obtain the confidence bounds on reliability. | The approximate reliability confidence bounds under the Modified Gompertz model can be obtained using nonlinear regression. Additionally, the reliability is always between 0 and 1. In order to keep the endpoints of the confidence interval, the logit transformation can be used to obtain the confidence bounds on reliability. | ||
::<math>CB=\frac{{{{\hat{R}}}_{i}}}{{{{\hat{R}}}_{i}}+(1-{{{\hat{R}}}_{i}}){{e}^{\pm {{z}_{\alpha }}{{{\hat{\sigma }}}_{R}}/\left[ {{{\hat{R}}}_{i}}(1-{{{\hat{R}}}_{i}}) \right]}}}</math> | ::<math>CB=\frac{{{{\hat{R}}}_{i}}}{{{{\hat{R}}}_{i}}+(1-{{{\hat{R}}}_{i}}){{e}^{\pm {{z}_{\alpha }}{{{\hat{\sigma }}}_{R}}/\left[ {{{\hat{R}}}_{i}}(1-{{{\hat{R}}}_{i}}) \right]}}}\,\!</math> | ||
::<math>{{\hat{\sigma }}^{2}}=\frac{SSE}{n-p}</math> | ::<math>{{\hat{\sigma }}^{2}}=\frac{SSE}{n-p}\,\!</math> | ||
where | where <math>p\,\!</math> is the total number of groups (in this case 4) and <math>n\,\!</math> is the total number of items in each group. | ||
==Example: Modified Gompertz for Reliability Data== | ==Example: Modified Gompertz for Reliability Data== | ||
| Line 741: | Line 741: | ||
& {{S}_{2}}(d)= & \underset{i=3}{\overset{5}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ | & {{S}_{2}}(d)= & \underset{i=3}{\overset{5}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ | ||
& {{S}_{3}}(d)= & \underset{i=6}{\overset{8}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) | & {{S}_{3}}(d)= & \underset{i=6}{\overset{8}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::<math>c(d)={{\left[ \frac{{{S}_{3}}(d)-{{S}_{2}}(d)}{{{S}_{2}}(d)-{{S}_{1}}(d)} \right]}^{\tfrac{1}{3}}}</math> | ::<math>c(d)={{\left[ \frac{{{S}_{3}}(d)-{{S}_{2}}(d)}{{{S}_{2}}(d)-{{S}_{1}}(d)} \right]}^{\tfrac{1}{3}}}\,\!</math> | ||
::<math>a(d)={{e}^{\left[ \tfrac{1}{3}\left( {{S}_{1}}(d)+\tfrac{{{S}_{2}}(d)-{{S}_{1}}(d)}{1-{{[c(d)]}^{3}}} \right) \right]}}</math> | ::<math>a(d)={{e}^{\left[ \tfrac{1}{3}\left( {{S}_{1}}(d)+\tfrac{{{S}_{2}}(d)-{{S}_{1}}(d)}{1-{{[c(d)]}^{3}}} \right) \right]}}\,\!</math> | ||
::<math>b(d)={{e}^{\left[ \tfrac{({{S}_{2}}(d)-{{S}_{1}}(d))(c(d)-1)}{{{\left[ 1-{{[c(d)]}^{3}} \right]}^{2}}} \right]}}</math> | ::<math>b(d)={{e}^{\left[ \tfrac{({{S}_{2}}(d)-{{S}_{1}}(d))(c(d)-1)}{{{\left[ 1-{{[c(d)]}^{3}} \right]}^{2}}} \right]}}\,\!</math> | ||
:and: | :and: | ||
::<math>{{R}_{0}}=d+a(d)\cdot b(d)</math> | ::<math>{{R}_{0}}=d+a(d)\cdot b(d)\,\!</math> | ||
where | where <math>{{R}_{0}}=31%\,\!</math>. Then, Eqn. (eq27) may be rewritten as: | ||
::<math>d-31+a(d)\cdot b(d)=0</math> | ::<math>d-31+a(d)\cdot b(d)=0\,\!</math> | ||
Eqns. (eq24), (eq25), (eq26) and (eq28) can now be solved simultaneously. One method for solving these equations numerically is to substitute different values of | Eqns. (eq24), (eq25), (eq26) and (eq28) can now be solved simultaneously. One method for solving these equations numerically is to substitute different values of <math>d\,\!</math>, which must be less than <math>{{R}_{0}}\,\!</math>, into Eqn. (eq28) and plot along the y-axis with the value of <math>d\,\!</math> along the x-axis. The value of <math>d\,\!</math> can then be read from the x-intercept. This can be repeated for greater accuracy using smaller and smaller increments of <math>d\,\!</math>. Once the desired accuracy on <math>d\,\!</math> has been achieved, the value of <math>d\,\!</math> can then be substituted into Eqns. (eq24), (eq25) and (eq26). Now <math>a\,\!</math>, <math>b\,\!</math> and <math>c\,\!</math> can be calculated. For this case, the initial estimates of the parameters are: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 764: | Line 764: | ||
\widehat{c}= & 0.46012 \\ | \widehat{c}= & 0.46012 \\ | ||
\widehat{d}= & 30.825 | \widehat{d}= & 30.825 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
Now, since the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting | Now, since the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting <math>{{Y}_{i}}={{R}_{i}},\,\!</math> <math>g_{1}^{(0)}=69.324,\,\!</math> <math>g_{2}^{(0)}=0.002524,\,\!</math> <math>g_{3}^{(0)}=0.46012,\,\!</math> and <math>g_{4}^{(0)}=30.825\,\!</math>, <math>{{Y}^{(0)}},{{D}^{(0)}},\,\!</math> <math>{{\nu }^{(0)}}\,\!</math> become: | ||
::<math>{{Y}^{(0)}}=\left[ \begin{matrix} | ::<math>{{Y}^{(0)}}=\left[ \begin{matrix} | ||
| Line 778: | Line 778: | ||
0.238155 \\ | 0.238155 \\ | ||
-0.320890 \\ | -0.320890 \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
::<math>{{D}^{(0)}}=\left[ \begin{matrix} | ::<math>{{D}^{(0)}}=\left[ \begin{matrix} | ||
| Line 790: | Line 790: | ||
0.974220 & 116.829 & -26.8352 & 1 \\ | 0.974220 & 116.829 & -26.8352 & 1 \\ | ||
0.988055 & 54.5185 & -14.3117 & 1 \\ | 0.988055 & 54.5185 & -14.3117 & 1 \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
::<math>{{\nu }^{(0)}}=\left[ \begin{matrix} | ::<math>{{\nu }^{(0)}}=\left[ \begin{matrix} | ||
| Line 802: | Line 802: | ||
0.46012 \\ | 0.46012 \\ | ||
30.825 \\ | 30.825 \\ | ||
\end{matrix} \right]</math> | \end{matrix} \right]\,\!</math> | ||
The estimate of the parameters | The estimate of the parameters <math>{{\nu }^{(0)}}\,\!</math> is given by: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 814: | Line 814: | ||
0.209458 \\ | 0.209458 \\ | ||
\end{matrix} \right] | \end{matrix} \right] | ||
\end{align}</math> | \end{align}\,\!</math> | ||
The revised estimated regression coefficients in matrix form are given by: | The revised estimated regression coefficients in matrix form are given by: | ||
| Line 837: | Line 837: | ||
31.0345 \\ | 31.0345 \\ | ||
\end{matrix} \right] | \end{matrix} \right] | ||
\end{align}</math> | \end{align}\,\!</math> | ||
With the starting coefficients | With the starting coefficients <math>{{g}^{(0)}}\,\!</math>, <math>Q\,\!</math> is: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
{{Q}^{(0)}}= & \underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(0)}}) \right)}^{2}} \\ | {{Q}^{(0)}}= & \underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(0)}}) \right)}^{2}} \\ | ||
= & 2.403672 | = & 2.403672 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
With the coefficients at the end of the first iteration, | With the coefficients at the end of the first iteration, <math>{{g}^{(1)}}\,\!</math>, <math>Q\,\!</math> is: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
{{Q}^{(1)}}= & \underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(1)}} \right) \right]}^{2}} \\ | {{Q}^{(1)}}= & \underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(1)}} \right) \right]}^{2}} \\ | ||
= & 2.073964 | = & 2.073964 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
Therefore: | Therefore: | ||
| Line 857: | Line 857: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
{{Q}^{(1)}}<{{Q}^{(0)}} | {{Q}^{(1)}}<{{Q}^{(0)}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
Hence, the Gauss-Newton method works in the right direction. The iterations are continued until the relationship of Eqn. (critir) has been satisfied. Using RGA, the estimators of the parameters are: | Hence, the Gauss-Newton method works in the right direction. The iterations are continued until the relationship of Eqn. (critir) has been satisfied. Using RGA, the estimators of the parameters are: | ||
| Line 866: | Line 866: | ||
\widehat{c}= & 0.4567 \\ | \widehat{c}= & 0.4567 \\ | ||
\widehat{d}= & 0.3104 | \widehat{d}= & 0.3104 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
Therefore, the Modified Gompertz model is: | Therefore, the Modified Gompertz model is: | ||
::<math>R=0.3104+(0.6904){{(0.0020)}^{{{0.4567}^{T}}}}</math> | ::<math>R=0.3104+(0.6904){{(0.0020)}^{{{0.4567}^{T}}}}\,\!</math> | ||
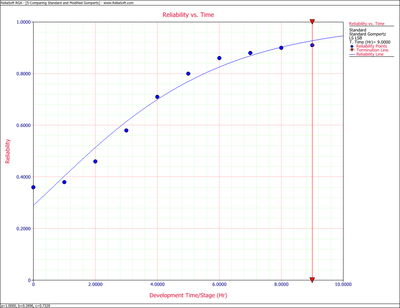
Using Eqn. (eq29), the predicted reliability is plotted in the following figure along with the raw data. It can be seen from the plot in the figure that the Modified Gompertz curve represents the data very well. | Using Eqn. (eq29), the predicted reliability is plotted in the following figure along with the raw data. It can be seen from the plot in the figure that the Modified Gompertz curve represents the data very well. | ||
| Line 881: | Line 881: | ||
:1) Estimate the parameters of the Standard Gompertz model. | :1) Estimate the parameters of the Standard Gompertz model. | ||
:2) What is the initial reliability at | :2) What is the initial reliability at <math>T=0\,\!</math> ? | ||
:3) Determine the reliability at the end of the ninth stage and check to see if the goal has been met. | :3) Determine the reliability at the end of the ninth stage and check to see if the goal has been met. | ||
| Line 915: | Line 915: | ||
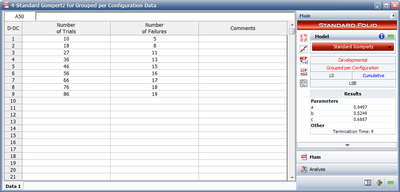
[[Image:rga7.6.png|thumb|center|400px|Entered data and the estimated Standard Gompertz parameters.]] | [[Image:rga7.6.png|thumb|center|400px|Entered data and the estimated Standard Gompertz parameters.]] | ||
:2) The initial reliability at | :2) The initial reliability at <math>T=0\,\!</math> is equal to: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 921: | Line 921: | ||
= & 0.9497\cdot 0.5249 \\ | = & 0.9497\cdot 0.5249 \\ | ||
= & 0.4985 | = & 0.4985 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
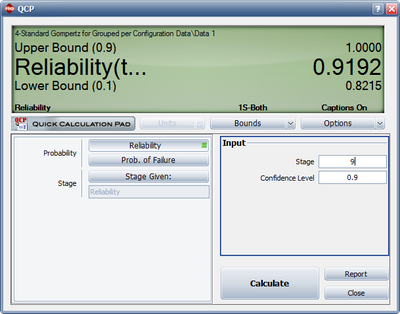
:3) The reliability at the ninth stage can be calculated using the Quick Calculation Pad (QCP) as shown in the figure below. | :3) The reliability at the ninth stage can be calculated using the Quick Calculation Pad (QCP) as shown in the figure below. | ||
Revision as of 20:46, 14 September 2012
This chapter discusses the two Gompertz models that are used in RGA. The Standard Gompertz and the Modified Gompertz.
The Standard Gompertz Model
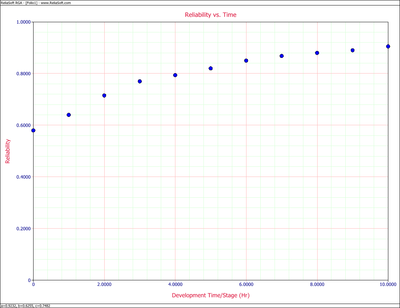
The Gompertz reliability growth model is often used when analyzing reliability data. It is most applicable when the data set follows a smooth curve, as shown in the plot below.
The Gompertz model is mathematically given by Virene [1]:
- [math]\displaystyle{ R=a{{b}^{{{c}^{T}}}}\,\! }[/math]
where:
- [math]\displaystyle{ 0\lt a\le 1\,\! }[/math]
- [math]\displaystyle{ 0\lt b\lt 1\,\! }[/math]
- [math]\displaystyle{ 0\lt c\lt 1\,\! }[/math]
- [math]\displaystyle{ T\gt 0\,\! }[/math]
- [math]\displaystyle{ R=\,\! }[/math] the system's reliability at development time, launch number or stage number, [math]\displaystyle{ T\,\! }[/math].
- [math]\displaystyle{ a=\,\! }[/math] the upper limit that the reliability approaches asymptotically as [math]\displaystyle{ T\to \infty \,\! }[/math], or the maximum reliability that can be attained.
- [math]\displaystyle{ ab=\,\! }[/math] initial reliability at [math]\displaystyle{ T=0.\,\! }[/math]
- [math]\displaystyle{ c=\,\! }[/math] the growth pattern indicator (small values of [math]\displaystyle{ c\,\! }[/math] indicate rapid early reliability growth and large values of [math]\displaystyle{ c\,\! }[/math] indicate slow reliability growth).
As it can be seen from the mathematical definition, the Gompertz model is a 3-parameter model with the parameters [math]\displaystyle{ a\,\! }[/math], [math]\displaystyle{ b\,\! }[/math] and [math]\displaystyle{ c\,\! }[/math]. The solution for the parameters, given [math]\displaystyle{ {{T}_{i}}\,\! }[/math] and [math]\displaystyle{ {{R}_{i}}\,\! }[/math], is accomplished by fitting the best possible line through the data points. Many methods are available; all of which tend to be numerically intensive. When analyzing reliability data in the RGA software, you have the option to enter the reliability values in percent or in decimal format. However, [math]\displaystyle{ a\,\! }[/math] will always be returned in decimal format and not in percent. The estimated parameters in the RGA software are unitless. The next section presents an overview and background on some of the most commonly used algorithms/methods for obtaining these parameters.
Parameter Estimation
<PER LISA: ASK SME TO ADD SOME SORT OF INTRODUCTION THAT PREPARES THE READER FOR THE THREE SUBSECTIONS>
Linear Regression
The method of least squares requires that a straight line be fitted to a set of data points. If the regression is on [math]\displaystyle{ Y\,\! }[/math], then the sum of the squares of the vertical deviations from the points to the line is minimized. If the regression is on [math]\displaystyle{ X\,\! }[/math], the line is fitted to a set of data points such that the sum of the squares of the horizontal deviations from the points to the line is minimized. To illustrate the method, this section presents a regression on [math]\displaystyle{ Y\,\! }[/math]. Consider the linear model given by Seber and Wild [2]:
- [math]\displaystyle{ {{Y}_{i}}={{\widehat{\beta }}_{0}}+{{\widehat{\beta }}_{1}}{{X}_{i1}}+{{\widehat{\beta }}_{2}}{{X}_{i2}}+...+{{\widehat{\beta }}_{p}}{{X}_{ip}}\,\! }[/math]
or in matrix form where bold letters indicate matrices:
- [math]\displaystyle{ \begin{align} Y=X\beta \end{align}\,\! }[/math]
- where:
- [math]\displaystyle{ Y=\left[ \begin{matrix} {{Y}_{1}} \\ {{Y}_{2}} \\ \vdots \\ {{Y}_{N}} \\ \end{matrix} \right]\,\! }[/math]
- [math]\displaystyle{ X=\left[ \begin{matrix} 1 & {{X}_{1,1}} & \cdots & {{X}_{1,p}} \\ 1 & {{X}_{2,1}} & \cdots & {{X}_{2,p}} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & {{X}_{N,1}} & \cdots & {{X}_{N,p}} \\ \end{matrix} \right]\,\! }[/math]
- and:
- [math]\displaystyle{ \beta =\left[ \begin{matrix} {{\beta }_{0}} \\ {{\beta }_{1}} \\ \vdots \\ {{\beta }_{p}} \\ \end{matrix} \right]\,\! }[/math]
The vector [math]\displaystyle{ \beta \,\! }[/math] holds the values of the parameters. Now let [math]\displaystyle{ \widehat{\beta }\,\! }[/math] be the estimates of these parameters, or the regression coefficients. The vector of estimated regression coefficients is denoted by:
- [math]\displaystyle{ \widehat{\beta }=\left[ \begin{matrix} {{\widehat{\beta }}_{0}} \\ {{\widehat{\beta }}_{1}} \\ \vdots \\ {{\widehat{\beta }}_{p}} \\ \end{matrix} \right]\,\! }[/math]
Solving for [math]\displaystyle{ \beta \,\! }[/math] in Eqn. (linear) requires the analyst to left multiply both sides by the transpose of [math]\displaystyle{ X\,\! }[/math], [math]\displaystyle{ {{X}^{T}}\,\! }[/math] :
- [math]\displaystyle{ ({{X}^{T}}X)\widehat{\beta }={{X}^{T}}Y\,\! }[/math]
Now the term [math]\displaystyle{ ({{X}^{T}}X)\,\! }[/math] becomes a square and invertible matrix. Then taking it to the other side of the equation gives:
- [math]\displaystyle{ \widehat{\beta }=({{X}^{T}}X)^{-1}{{X}^{T}}Y\,\! }[/math]
Nonlinear Regression
Nonlinear regression is similar to linear regression, except that a curve is fitted to the data set instead of a straight line. Just as in the linear scenario, the sum of the squares of the horizontal and vertical distances between the line and the points are to be minimized. In the case of the nonlinear Gompertz model [math]\displaystyle{ R=a{{b}^{{{c}^{T}}}}\,\! }[/math], let:
- [math]\displaystyle{ {{Y}_{i}}=f({{T}_{i}},\delta )=a{{b}^{{{c}^{{{T}_{i}}}}}}\,\! }[/math]
- where:
- [math]\displaystyle{ {{T}_{i}}=\left[ \begin{matrix} {{T}_{1}} \\ {{T}_{2}} \\ \vdots \\ {{T}_{N}} \\ \end{matrix} \right],\quad i=1,2,...,N\,\! }[/math]
- and:
- [math]\displaystyle{ \delta =\left[ \begin{matrix} a \\ b \\ c \\ \end{matrix} \right]\,\! }[/math]
The Gauss-Newton method can be used to solve for the parameters [math]\displaystyle{ a\,\! }[/math], [math]\displaystyle{ b\,\! }[/math] and [math]\displaystyle{ c\,\! }[/math] by performing a Taylor series expansion on [math]\displaystyle{ f({{T}_{i}},\delta ).\,\! }[/math] Then approximate the nonlinear model with linear terms and employ ordinary least squares to estimate the parameters. This procedure is performed in an iterative manner and it generally leads to a solution of the nonlinear problem.
This procedure starts by using initial estimates of the parameters [math]\displaystyle{ a\,\! }[/math], [math]\displaystyle{ b\,\! }[/math] and [math]\displaystyle{ c\,\! }[/math], denoted as [math]\displaystyle{ g_{1}^{(0)},\,\! }[/math] [math]\displaystyle{ g_{2}^{(0)}\,\! }[/math] and [math]\displaystyle{ g_{3}^{(0)},\,\! }[/math] where [math]\displaystyle{ ^{(0)}\,\! }[/math] is the iteration number. The Taylor series expansion approximates the mean response, [math]\displaystyle{ f({{T}_{i}},\delta )\,\! }[/math], around the starting values, [math]\displaystyle{ g_{1}^{(0)},\,\! }[/math] [math]\displaystyle{ g_{2}^{(0)}\,\! }[/math] and [math]\displaystyle{ g_{3}^{(0)}.\,\! }[/math] For the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] observation:
- [math]\displaystyle{ f({{T}_{i}},\delta )\simeq f({{T}_{i}},{{g}^{(0)}})+\underset{k=1}{\overset{p}{\mathop \sum }}\,{{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}}({{\delta }_{k}}-g_{k}^{(0)})\,\! }[/math]
- where:
- [math]\displaystyle{ {{g}^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ \end{matrix} \right]\,\! }[/math]
- Let:
- [math]\displaystyle{ \begin{align} f_{i}^{(0)}= & f({{T}_{i}},{{g}^{(0)}}) \\ \nu _{k}^{(0)}= & ({{\delta }_{k}}-g_{k}^{(0)}) \\ D_{ik}^{(0)}= & {{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}} \end{align}\,\! }[/math]
So Eqn. (nl1) becomes:
- [math]\displaystyle{ {{Y}_{i}}\simeq f_{i}^{(0)}+\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}\,\! }[/math]
or by shifting [math]\displaystyle{ f_{i}^{(0)}\,\! }[/math] to the left of the equation:
- [math]\displaystyle{ Y_{i}^{(0)}\simeq \underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}\,\! }[/math]
In matrix form this is given by:
- [math]\displaystyle{ {{Y}^{(0)}}\simeq {{D}^{(0)}}{{\nu }^{(0)}}\,\! }[/math]
- where:
- [math]\displaystyle{ {{Y}^{(0)}}=\left[ \begin{matrix} {{Y}_{1}}-f_{1}^{(0)} \\ {{Y}_{2}}-f_{2}^{(0)} \\ \vdots \\ {{Y}_{N}}-f_{N}^{(0)} \\ \end{matrix} \right]=\left[ \begin{matrix} {{Y}_{1}}-g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{1}}}} \\ {{Y}_{1}}-g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{2}}}} \\ \vdots \\ {{Y}_{N}}-g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} \\ \end{matrix} \right]\,\! }[/math]
- and:
- [math]\displaystyle{ {{\nu }^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ \end{matrix} \right]\,\! }[/math]
Note that Eqn. (matr) is in the form of the general linear regression model of Eqn. (linear). According to Eqn. (lincoeff), the estimate of the parameters [math]\displaystyle{ {{\nu }^{(0)}}\,\! }[/math] is given by:
- [math]\displaystyle{ {{\widehat{\nu }}^{(0)}}={{\left( {{D}^{{{(0)}^{T}}}}{{D}^{(0)}} \right)}^{-1}}{{D}^{{{(0)}^{T}}}}{{Y}^{(0)}}\,\! }[/math]
The revised estimated regression coefficients in matrix form are:
- [math]\displaystyle{ {{g}^{(1)}}={{g}^{(0)}}+{{\widehat{\nu }}^{(0)}}\,\! }[/math]
The least squares criterion measure, [math]\displaystyle{ Q,\,\! }[/math] should be checked to examine whether the revised regression coefficients will lead to a reasonable result. According to the Least Squares Principle, the solution to the values of the parameters are those values that minimize [math]\displaystyle{ Q\,\! }[/math]. With the starting coefficients, [math]\displaystyle{ {{g}^{(0)}}\,\! }[/math], [math]\displaystyle{ Q\,\! }[/math] is:
- [math]\displaystyle{ {{Q}^{(0)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(0)}} \right) \right]}^{2}}\,\! }[/math]
And with the coefficients at the end of the first iteration, [math]\displaystyle{ {{g}^{(1)}}\,\! }[/math], [math]\displaystyle{ Q\,\! }[/math] is:
- [math]\displaystyle{ {{Q}^{(1)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(1)}} \right) \right]}^{2}}\,\! }[/math]
For the Gauss-Newton method to work properly and to satisfy the Least Squares Principle, the relationship [math]\displaystyle{ {{Q}^{(k+1)}}\lt {{Q}^{(k)}}\,\! }[/math] has to hold for all [math]\displaystyle{ k\,\! }[/math], meaning that [math]\displaystyle{ {{g}^{(k+1)}}\,\! }[/math] gives a better estimate than [math]\displaystyle{ {{g}^{(k)}}\,\! }[/math]. The problem is not yet completely solved. Now [math]\displaystyle{ {{g}^{(1)}}\,\! }[/math] are the starting values, producing a new set of values [math]\displaystyle{ {{g}^{(2)}}\,\! }[/math]. The process is continued until the following relationship has been satisfied:
- [math]\displaystyle{ {{Q}^{(s-1)}}-{{Q}^{(s)}}\simeq 0\,\! }[/math]
When using the Gauss-Newton method or some other estimation procedure, it is advisable to try several sets of starting values to make sure that the solution gives relatively consistent results.
Choice of Initial Values
The choice of the starting values for the nonlinear regression is not an easy task. A poor choice may result in a lengthy computation with many iterations. It may also lead to divergence, or to a convergence due to a local minimum. Therefore, good initial values will result in fast computations with few iterations and if multiple minima exist, it will lead to a solution that is a minimum.
Various methods were developed for obtaining valid initial values for the regression parameters. The following procedure is described by Virene [1] in estimating the Gompertz parameters. This procedure is rather simple. It will be used to get the starting values for the Gauss-Newton method, or for any other method that requires initial values. Some analysts are using this method to calculate the parameters if the data set is divisible into three groups of equal size. However, if the data set is not equally divisible, it can still provide good initial estimates.
Consider the case where [math]\displaystyle{ m\,\! }[/math] observations are available in the form shown next. Each reliability value, [math]\displaystyle{ {{R}_{i}}\,\! }[/math], is measured at the specified times, [math]\displaystyle{ {{T}_{i}}\,\! }[/math].
- [math]\displaystyle{ \begin{matrix} {{T}_{i}} & {{R}_{i}} \\ {{T}_{0}} & {{R}_{0}} \\ {{T}_{1}} & {{R}_{1}} \\ {{T}_{2}} & {{R}_{2}} \\ \vdots & \vdots \\ {{T}_{m-1}} & {{R}_{m-1}} \\ \end{matrix}\,\! }[/math]
- where:
- [math]\displaystyle{ m=3n,\,\! }[/math] [math]\displaystyle{ n\,\! }[/math] is equal to the number of items in each equally sized group
- [math]\displaystyle{ {{T}_{i}}-{{T}_{i-1}}=const\,\! }[/math]
- [math]\displaystyle{ i=0,1,...,m-1\,\! }[/math]
The Gompertz reliability equation is given by:
- [math]\displaystyle{ R=a{{b}^{{{c}^{T}}}}\,\! }[/math]
- and:
- [math]\displaystyle{ \begin{align} \ln (R)=\ln (a)+{{c}^{T}}\ln (b) \end{align}\,\! }[/math]
- Define:
- [math]\displaystyle{ S_1=\sum_{i=0}^{n-1} ln(R_i)= n ln(a)+ln(b)\sum_{i=0}^{n-1} c^{T_i}\,\! }[/math]
- [math]\displaystyle{ S_2=\sum_{i=n}^{2n-1} ln(R_i)= n ln(a)+ln(b)\sum_{i=n}^{2n-1} c^{T_i}\,\! }[/math]
- [math]\displaystyle{ S_3=\sum_{i=2n}^{m-1} ln(R_i)= n ln(a)+ln(b)\sum_{i=2n}^{m-1} c^{T_i}\,\! }[/math]
- Then:
- [math]\displaystyle{ \frac{S_3-S_2}{S_2-S_1}=\frac{\sum_{i=2n}{m-1} c^{T_i}-\sum_{i=n}^{2n-1} c^T_i}{\sum_{i=0}^{n-1} c^{T_i}}\,\! }[/math]
- [math]\displaystyle{ \frac{S_3-S_2}{S_2-S_1}=c^T_{2n}\frac{\sum_{i=0}{n-1} c^{T_i}-c^{T_n}\sum_{i=0}^{n-1} c^T_i}{c^{T_n}\sum_{i=0}^{n-1} c^{T_i}}\,\! }[/math]
- [math]\displaystyle{ \frac{S_3 - S_2}{S_2-S_1}=\frac{c^{T_2n}-c^{T_n}}{c^{T_n}-1}=c^{T_{a_n}}=c^{n\cdot I+T_0}\,\! }[/math]
Without loss of generality, take [math]\displaystyle{ {{T}_{{{a}_{0}}}}=0\,\! }[/math] ; then:
- [math]\displaystyle{ \frac{{{S}_{3}}-{{S}_{2}}}{{{S}_{2}}-{{S}_{1}}}={{c}^{n\cdot I}}\,\! }[/math]
Solving for [math]\displaystyle{ c\,\! }[/math] yields:
<<NEED TO ADD AN EQUATION>>
Considering Eqns. (gomp3a) and (gomp3b), then:
- [math]\displaystyle{ \begin{align} {{S}_{1}}-n\cdot \ln (a)= & \ln (b)\underset{i=0}{\overset{n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \\ {{S}_{2}}-n\cdot \ln (a)= & \ln (b)\underset{i=n}{\overset{2n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \end{align}\,\! }[/math]
- or:
- [math]\displaystyle{ \frac{{{S}_{1}}-n\cdot \ln (a)}{{{S}_{2}}-n\cdot \ln (a)}=\frac{1}{{{c}^{n\cdot I}}}\,\! }[/math]
Reordering the equation yields:
- [math]\displaystyle{ \begin{align} \ln (a)= & \frac{1}{n}\left( {{S}_{1}}+\frac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n\cdot I}}} \right) \\ a= & {{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}+\tfrac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n\cdot I}}} \right) \right]}} \end{align}\,\! }[/math]
If the reliability values are in percent then [math]\displaystyle{ a\,\! }[/math] needs to be divided by 100 to return the estimate in decimal format. Consider Eqns. (gomp3a) and (gomp3b) again, where:
<<NEED TO ADD AN EQUATION>>
Reordering Eqn. (gomp6) yields:
- [math]\displaystyle{ \begin{align} \ln (b)= & \frac{({{S}_{2}}-{{S}_{1}})({{c}^{I}}-1)}{{{(1-{{c}^{n\cdot I}})}^{2}}} \\ b= & {{e}^{\left[ \tfrac{\left( {{S}_{2}}-{{S}_{1}} \right)\left( {{c}^{I}}-1 \right)}{{{\left( 1-{{c}^{n\cdot I}} \right)}^{2}}} \right]}} \end{align}\,\! }[/math]
For the special case where [math]\displaystyle{ I=1\,\! }[/math], from Eqns. (gomp4), (gomp5) and (gomp7), the parameters are:
- [math]\displaystyle{ \begin{align} c= & {{\left( \frac{{{S}_{3}}-{{S}_{2}}}{{{S}_{2}}-{{S}_{1}}} \right)}^{\tfrac{1}{n}}} \\ a= & {{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}+\tfrac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n}}} \right) \right]}} \\ b= & {{e}^{\left[ \tfrac{({{S}_{2}}-{{S}_{1}})(c-1)}{{{\left( 1-{{c}^{n}} \right)}^{2}}} \right]}} \end{align}\,\! }[/math]
To estimate the values of the parameters [math]\displaystyle{ a,b\,\! }[/math] and [math]\displaystyle{ c\,\! }[/math], do the following:
- 1) Arrange the currently available data in terms of [math]\displaystyle{ T\,\! }[/math] and [math]\displaystyle{ R\,\! }[/math] as in the table below. The [math]\displaystyle{ T\,\! }[/math] values should be chosen at equal intervals and increasing in value by 1, such as one month, one hour, etc.
| Group Number | Growth Time [math]\displaystyle{ T\,\! }[/math](months) | Reliability [math]\displaystyle{ R\,\! }[/math](%) | [math]\displaystyle{ \ln{R}\,\! }[/math] |
|---|---|---|---|
| 0 | 58 | 4.060 | |
| 1 | 1 | 66 | 4.190 |
| [math]\displaystyle{ {{S}_{1}}\,\! }[/math] = 8.250 | |||
| 2 | 72.5 | 4.284 | |
| 2 | 3 | 78 | 4.357 |
| [math]\displaystyle{ {{S}_{2}}\,\! }[/math] = 8.641 | |||
| 4 | 82 | 4.407 | |
| 3 | 5 | 85 | 4.443 |
| [math]\displaystyle{ {{S}_{3}}\,\! }[/math] = 8.850 |
- 2) Calculate the natural log [math]\displaystyle{ R\,\! }[/math].
- 3) Divide the column of values for log [math]\displaystyle{ R\,\! }[/math] into three groups of equal size, each containing [math]\displaystyle{ n\,\! }[/math] items. There should always be three groups. Each group should always have the same number, [math]\displaystyle{ n\,\! }[/math], of items, measurements or values.
- 4) Add the values of the natural log [math]\displaystyle{ R\,\! }[/math] in each group, obtaining the sums identified as [math]\displaystyle{ {{S}_{1}}\,\! }[/math], [math]\displaystyle{ {{S}_{2}}\,\! }[/math] and [math]\displaystyle{ {{S}_{3}}\,\! }[/math], starting with the lowest values of the natural log [math]\displaystyle{ R\,\! }[/math].
- 5) Calculate [math]\displaystyle{ c\,\! }[/math] from Eqn. (eq9):
- [math]\displaystyle{ c={{\left( \frac{{{S}_{3}}-{{S}_{2}}}{{{S}_{2}}-{{S}_{1}}} \right)}^{\tfrac{1}{n}}}\,\! }[/math]
- 6) Calculate [math]\displaystyle{ a\,\! }[/math] from Eqn. (eq10):
- [math]\displaystyle{ a={{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}+\tfrac{{{S}_{2}}-{{S}_{1}}}{1-{{c}^{n}}} \right) \right]}}\,\! }[/math]
- 7) Calculate [math]\displaystyle{ b\,\! }[/math] from Eqn. (eq11):
- [math]\displaystyle{ b={{e}^{\left[ \tfrac{({{S}_{2}}-{{S}_{1}})(c-1)}{{{\left( 1-{{c}^{n}} \right)}^{2}}} \right]}}\,\! }[/math]
- 8) Write the Gompertz reliability growth equation.
- 9) Substitute the value of [math]\displaystyle{ T\,\! }[/math], the time at which the reliability goal is to be achieved, to see if the reliability is indeed to be attained or exceeded by [math]\displaystyle{ T\,\! }[/math].
Confidence Bounds
The approximate reliability confidence bounds under the Gompertz model can be obtained with nonlinear regression. Additionally, the reliability is always between 0 and 1. In order to keep the endpoints of the confidence interval, the logit transformation is used to obtain the confidence bounds on reliability.
- [math]\displaystyle{ CB=\frac{{{{\hat{R}}}_{i}}}{{{{\hat{R}}}_{i}}+(1-{{{\hat{R}}}_{i}}){{e}^{\pm {{z}_{\alpha }}{{{\hat{\sigma }}}_{R}}/\left[ {{{\hat{R}}}_{i}}(1-{{{\hat{R}}}_{i}}) \right]}}}\,\! }[/math]
- [math]\displaystyle{ {{\hat{\sigma }}^{2}}=\frac{SSE}{n-p}\,\! }[/math]
where [math]\displaystyle{ p\,\! }[/math] is the total number of groups (in this case 3) and [math]\displaystyle{ n\,\! }[/math] is the total number of items in each group.
Example: Standard Gompertz for Reliability Data
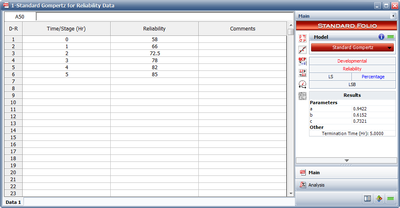
A device is required to have a reliability of 92% at the end of a 12-month design and development period. The following table gives the data obtained for the first five moths.
- 1) What will the reliability be at the end of this 12-month period?
- 2) What will the maximum achievable reliability be if the reliability program plan pursued during the first 5 months is continued?
- 3) How do the predicted reliability values compare with the actual values?
| Group Number | Growth Time [math]\displaystyle{ T\,\! }[/math](months) | Reliability [math]\displaystyle{ R\,\! }[/math](%) | [math]\displaystyle{ \ln{R}\,\! }[/math] |
|---|---|---|---|
| 0 | 58 | 4.060 | |
| 1 | 1 | 66 | 4.190 |
| [math]\displaystyle{ {{S}_{1}}\,\! }[/math] = 8.250 | |||
| 2 | 72.5 | 4.284 | |
| 2 | 3 | 78 | 4.357 |
| [math]\displaystyle{ {{S}_{2}}\,\! }[/math] = 8.641 | |||
| 4 | 82 | 4.407 | |
| 3 | 5 | 85 | 4.443 |
| [math]\displaystyle{ {{S}_{3}}\,\! }[/math] = 8.850 |
Solution
Having completed Steps 1 through 4 by preparing the table and calculating the last column to find [math]\displaystyle{ {{S}_{1}}\,\! }[/math], [math]\displaystyle{ {{S}_{2}}\,\! }[/math] and [math]\displaystyle{ {{S}_{3}}\,\! }[/math], proceed as follows:
- a) Find [math]\displaystyle{ c\,\! }[/math] from Eqn. (eq9).
- [math]\displaystyle{ \begin{align} c= & {{\left( \frac{8.850-8.641}{8.641-8.250} \right)}^{\tfrac{1}{2}}} \\ = & 0.731 \end{align}\,\! }[/math]
- b) Find [math]\displaystyle{ a\,\! }[/math] from Eqn. (eq10).
- This is the upper limit for the reliability as [math]\displaystyle{ T\to \infty \,\! }[/math].
- c) Find [math]\displaystyle{ b\,\! }[/math] from Eqn. (eq11).
- [math]\displaystyle{ \begin{align} b= & {{e}^{\left[ \tfrac{(8.641-8.250)(0.731-1)}{{{(1-{{0.731}^{2}})}^{2}}} \right]}} \\ = & {{e}^{(-0.485)}} \\ = & 0.615 \end{align}\,\! }[/math]
- Now, since the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting [math]\displaystyle{ {{Y}_{i}}={{R}_{i}},\,\! }[/math] [math]\displaystyle{ g_{1}^{(0)}=94.16,\,\! }[/math] [math]\displaystyle{ g_{2}^{(0)}=0.615,\,\! }[/math] [math]\displaystyle{ g_{3}^{(0)}=0.731,\,\! }[/math] [math]\displaystyle{ {{Y}^{(0)}},{{D}^{(0)}},\,\! }[/math] [math]\displaystyle{ {{\nu }^{(0)}}\,\! }[/math] become:
- [math]\displaystyle{ {{Y}^{(0)}}=\left[ \begin{matrix} 0.0916 \\ 0.0015 \\ -0.1190 \\ 0.1250 \\ 0.0439 \\ -0.0743 \\ \end{matrix} \right]\,\! }[/math]
- [math]\displaystyle{ {{D}^{(0)}}=\left[ \begin{matrix} 0.6150 & 94.1600 & 0.0000 \\ 0.7009 & 78.4470 & -32.0841 \\ 0.7712 & 63.0971 & -51.6122 \\ 0.8270 & 49.4623 & -60.6888 \\ 0.8704 & 38.0519 & -62.2513 \\ 0.9035 & 28.8742 & -59.0463 \\ \end{matrix} \right]\,\! }[/math]
- [math]\displaystyle{ {{\nu }^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ \end{matrix} \right]=\left[ \begin{matrix} 94.16 \\ 0.615 \\ 0.731 \\ \end{matrix} \right]\,\! }[/math]
The estimate of the parameters [math]\displaystyle{ {{\nu }^{(0)}}\,\! }[/math] is given by:
The revised estimated regression coefficients in matrix form are:
- [math]\displaystyle{ \begin{align} {{Q}^{(k+1)}}\lt {{Q}^{(k)}} \end{align}\,\! }[/math]
If the Gauss-Newton method works effectively, then the relationship has to hold, meaning that [math]\displaystyle{ {{g}^{(k+1)}}\,\! }[/math] gives better estimates than [math]\displaystyle{ {{g}^{(k)}}\,\! }[/math], after [math]\displaystyle{ k\,\! }[/math]. With the starting coefficients, [math]\displaystyle{ {{g}^{(0)}},\,\! }[/math] [math]\displaystyle{ Q\,\! }[/math] is:
And with the coefficients at the end of the first iteration, [math]\displaystyle{ {{g}^{(1)}},\,\! }[/math] [math]\displaystyle{ Q\,\! }[/math] is:
Therefore, it can be justified that the Gauss-Newton method works in the right direction. The iterations are continued until the relationship of Eqn.(crit) is satisfied. Note that the RGA siftware uses a different analysis method called the Levenberg-Marquardt. This method utilizes the best features of the Gauss-Newton method and the method of the steepest descent, and occupies a middle ground between these two methods. The estimated parameters using RGA are shown in the figure below.
They are:
- [math]\displaystyle{ \begin{align} & \widehat{a}= & 0.9422 \\ & \widehat{b}= & 0.6152 \\ & \widehat{c}= & 0.7321 \end{align}\,\! }[/math]
The Gompertz reliability growth curve is:
- [math]\displaystyle{ R=0.9422{{(0.6152)}^{{{0.7321}^{T}}}}\,\! }[/math]
- 1) The achievable reliability at the end of the 12-month period of design and development is:
The required reliability is 92%. Consequently, from the previous result, this requirement will barely be met. Every effort should therefore be expended to implement the reliability program plan fully, and perhaps augment it slightly to assure that the reliability goal will be met.
- 2) The maximum achievable reliability from Step 2, or from the value of [math]\displaystyle{ a\,\! }[/math], is 0.9422.
- 3) The predicted reliability values, as calculated from the Gompertz equation, Eqn. (eq8), are compared with the actual data in the table below. It may be seen in the table that the Gompertz curve appears to provide a very good fit for the data used because the equation reproduces the available data with less than 1% error. Eqn. (eq8) is plotted in the figure below the table and identifies the type of reliability growth curve this equation represents.
| Growth Time [math]\displaystyle{ T\,\! }[/math](months) | Gompertz Reliability(%) | Raw Data Reliability(%) |
|---|---|---|
| 0 | 57.97 | 58.00 |
| 1 | 66.02 | 66.00 |
| 2 | 72.62 | 72.50 |
| 3 | 77.87 | 78.00 |
| 4 | 81.95 | 82.00 |
| 5 | 85.07 | 85.00 |
| 6 | 87.43 | |
| 7 | 89.20 | |
| 8 | 90.52 | |
| 9 | 91.50 | |
| 10 | 92.22 | |
| 11 | 92.75 | |
| 12 | 93.14 |
Example: Standard Gompertz for Sequential Data
Calculate the parameters of the Gompertz model using the sequential data in the following table.
| Run Number | Result | Successes | Observed Reliability(%) |
|---|---|---|---|
| 1 | F | 0 | |
| 2 | F | 0 | |
| 3 | F | 0 | |
| 4 | S | 1 | 25.00 |
| 5 | F | 1 | 20.00 |
| 6 | F | 1 | 16.67 |
| 7 | S | 2 | 28.57 |
| 8 | S | 3 | 37.50 |
| 9 | S | 4 | 44.44 |
| 10 | S | 5 | 50.00 |
| 11 | S | 6 | 54.55 |
| 12 | S | 7 | 58.33 |
| 13 | S | 8 | 61.54 |
| 14 | S | 9 | 64.29 |
| 15 | S | 10 | 66.67 |
| 16 | S | 11 | 68.75 |
| 17 | F | 11 | 64.71 |
| 18 | S | 12 | 66.67 |
| 19 | F | 12 | 63.16 |
| 20 | S | 13 | 65.00 |
| 21 | S | 14 | 66.67 |
| 22 | S | 15 | 68.18 |
Solution Using RGA, the parameter estimates are shown in the following figure.
Cumulative Reliability
<PER LISA: ASK SME HOW THIS FITS IN. IS IT A SUBSECTION FOR STANDARD GOMPERTZ OR DOES IT APPLY TO BOTH?> For many kinds of equipment, especially missiles and space systems, only success/failure data (also called discrete or attribute data) is obtained. Conservatively, the cumulative reliability can be used to estimate the trend of reliability growth. The cumulative reliability is given by Kececioglu [3]:
- [math]\displaystyle{ \bar{R}(N)=\frac{N-r}{N}\,\! }[/math]
where:
- [math]\displaystyle{ N\,\! }[/math] is the current number of trials
- [math]\displaystyle{ r\,\! }[/math] is the number of failures
It must be emphasized that the instantaneous reliability of the developed equipment is increasing as the test-analyze-fix-and-test process continues. In addition, the instantaneous reliability is higher than the cumulative reliability. Therefore, the reliability growth curve based on the cumulative reliability can be thought of as the lower bound of the true reliability growth curve.
The Modified Gompertz Model
Sometimes reliability growth data with an S-shaped trend cannot be described accurately by the Standard Gompertz or Logistic curves. Because these two models have fixed values of reliability at the inflection points, only a few reliability growth data sets following an S-shaped reliability growth curve can be fitted to them. A modification of the Gompertz curve, which overcomes this shortcoming, is given next [5].
If we apply a shift in the vertical coordinate, then the Gompertz model is defined by:
- [math]\displaystyle{ R=d+a{{b}^{{{c}^{T}}}}\,\! }[/math]
where:
- [math]\displaystyle{ 0\lt a+d\le 1\,\! }[/math]
- [math]\displaystyle{ 0\lt b\lt 1,0\lt c\lt 1,\text{and}T\ge 0\,\! }[/math]
- [math]\displaystyle{ R\,\! }[/math] is the system's reliability at development time [math]\displaystyle{ T\,\! }[/math] or at launch number [math]\displaystyle{ T\,\! }[/math], or stage number [math]\displaystyle{ T\,\! }[/math].
- [math]\displaystyle{ d\,\! }[/math] is the shift parameter.
- [math]\displaystyle{ d+a\,\! }[/math] is the upper limit that the reliability approaches asymptotically as [math]\displaystyle{ T\to\infty\,\! }[/math]
- [math]\displaystyle{ d+ab\,\! }[/math] is the initial reliability at [math]\displaystyle{ T=0\,\! }[/math]
- [math]\displaystyle{ c\,\! }[/math] is the growth pattern indicator(small values of [math]\displaystyle{ c\,\! }[/math] indicate rapid early reliability growth and large values of [math]\displaystyle{ c\,\! }[/math] indicate slow reliability growth).
The Modified Gompertz model is more flexible than the original, especially when fitting growth data with S-shaped trends.
Parameter Estimation
To implement the Modified Gompertz growth model, initial values of the parameters [math]\displaystyle{ a\,\! }[/math], [math]\displaystyle{ b\,\! }[/math], [math]\displaystyle{ c\,\! }[/math] and [math]\displaystyle{ d\,\! }[/math] must be determined. When analyzing reliability data in RGA, you have the option to enter the reliability values in percent or in decimal format. However, [math]\displaystyle{ a\,\! }[/math] and [math]\displaystyle{ d\,\! }[/math] will always be returned in decimal format and not in percent. The estimated parameters in RGA are unitless.
Given that [math]\displaystyle{ R=d+a{{b}^{{{c}^{T}}}}\,\! }[/math] and [math]\displaystyle{ \ln (R-d)=\ln (a)+{{c}^{T}}\ln (b)\,\! }[/math], it follows that [math]\displaystyle{ {{S}_{1}}\,\! }[/math], [math]\displaystyle{ {{S}_{2}}\,\! }[/math] and [math]\displaystyle{ {{S}_{3}}\,\! }[/math], as defined in the derivation of the Standard Gompertz model, can be expressed as functions of [math]\displaystyle{ d\,\! }[/math].
- [math]\displaystyle{ \begin{align} {{S}_{1}}(d)= & \underset{i=0}{\overset{n-1}{\mathop \sum }}\,\ln ({{R}_{i}}-d)=n\ln (a)+\ln (b)\underset{i=0}{\overset{n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \\ {{S}_{2}}(d)= & \underset{i=n}{\overset{2n-1}{\mathop \sum }}\,\ln ({{R}_{i}}-d)=n\ln (a)+\ln (b)\underset{i=n}{\overset{2n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \\ {{S}_{3}}(d)= & \underset{i=2n}{\overset{m-1}{\mathop \sum }}\,\ln ({{R}_{i}}-d)=n\ln (a)+\ln (b)\underset{i=2n}{\overset{m-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \end{align}\,\! }[/math]
Modifying the equations given above in the Standard Gompertz Parameter Estimation section as functions of [math]\displaystyle{ d\,\! }[/math] yields:
- [math]\displaystyle{ \begin{align} c(d)= & {{\left[ \frac{{{S}_{3}}(d)-{{S}_{2}}(d)}{{{S}_{2}}(d)-{{S}_{1}}(d)} \right]}^{\tfrac{1}{n\cdot I}}} \\ a(d)= & {{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}(d)+\tfrac{{{S}_{2}}(d)-{{S}_{1}}(d)}{1-{{[c(d)]}^{n\cdot I}}} \right) \right]}} \\ b(d)= & {{e}^{\left[ \tfrac{\left[ {{S}_{2}}(d)-{{S}_{1}}(d) \right]\left[ {{[c(d)]}^{I}}-1 \right]}{{{\left[ 1-{{[c(d)]}^{n\cdot I}} \right]}^{2}}} \right]}} \end{align}\,\! }[/math]
where [math]\displaystyle{ I\,\! }[/math] is the time interval increment. At this point, you can use the initial constraint of:
- [math]\displaystyle{ \begin{align} d+ab=\text{original level of reliability at }T=0 \end{align}\,\! }[/math]
Now there are four equations, Eqns. (eq17), (eq18), (eq19) and (eq20), and four unknowns, [math]\displaystyle{ a\,\! }[/math], [math]\displaystyle{ b\,\! }[/math], [math]\displaystyle{ c\,\! }[/math] and [math]\displaystyle{ d\,\! }[/math]. The simultaneous solution of these equations yields the four initial values for the parameters of the Modified Gompertz model. This procedure is similar to the one discussed before. It starts by using initial estimates of the parameters, [math]\displaystyle{ a\,\! }[/math], [math]\displaystyle{ b\,\! }[/math], [math]\displaystyle{ c\,\! }[/math] and [math]\displaystyle{ d\,\! }[/math], denoted as [math]\displaystyle{ g_{1}^{(0)},\,\! }[/math] [math]\displaystyle{ g_{2}^{(0)},\,\! }[/math] [math]\displaystyle{ g_{3}^{(0)},\,\! }[/math] and [math]\displaystyle{ g_{4}^{(0)},\,\! }[/math] where [math]\displaystyle{ ^{(0)}\,\! }[/math] is the iteration number.
The Taylor series expansion approximates the mean response, [math]\displaystyle{ f({{T}_{i}},\delta )\,\! }[/math], around the starting values, [math]\displaystyle{ g_{1}^{(0)},\,\! }[/math] [math]\displaystyle{ g_{2}^{(0)},\,\! }[/math] [math]\displaystyle{ g_{3}^{(0)}\,\! }[/math] and [math]\displaystyle{ g_{4}^{(0)}\,\! }[/math]. For the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] observation:
- [math]\displaystyle{ f({{T}_{i}},\delta )\simeq f({{T}_{i}},{{g}^{(0)}})+\underset{k=1}{\overset{p}{\mathop \sum }}\,{{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}}\cdot ({{\delta }_{k}}-g_{k}^{(0)})\,\! }[/math]
- where:
- [math]\displaystyle{ {{g}^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ g_{4}^{(0)} \\ \end{matrix} \right]\,\! }[/math]
- Let:
- [math]\displaystyle{ \begin{align} f_{i}^{(0)}= & f({{T}_{i}},{{g}^{(0)}}) \\ \nu _{k}^{(0)}= & ({{\delta }_{k}}-g_{k}^{(0)}) \\ D_{ik}^{(0)}= & {{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}} \end{align}\,\! }[/math]
- Therefore:
- [math]\displaystyle{ {{Y}_{i}}=f_{i}^{(0)}+\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}\,\! }[/math]
or by shifting [math]\displaystyle{ f_{i}^{(0)}\,\! }[/math] to the left of the equation:
- [math]\displaystyle{ Y_{i}^{(0)}-f_{i}^{(0)}=\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)}\,\! }[/math]
In matrix form, this is given by:
- [math]\displaystyle{ {{Y}^{(0)}}\simeq {{D}^{(0)}}{{\nu }^{(0)}}\,\! }[/math]
where:
- [math]\displaystyle{ {{Y}^{(0)}}=\left[ \begin{matrix} {{Y}_{1}}-f_{1}^{(0)} \\ . \\ . \\ {{Y}_{N}}-f_{N}^{(0)} \\ \end{matrix} \right]=\left[ \begin{matrix} {{Y}_{1}}-g_{4}^{(0)}+g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{1}}}} \\ . \\ . \\ {{Y}_{N}}-g_{4}^{(0)}+g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} \\ \end{matrix} \right]\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{D}^{(0)}}= & \left[ \begin{matrix} D_{11}^{(0)} & D_{12}^{(0)} & D_{13}^{(0)} & D_{14}^{(0)} \\ . & . & . & . \\ . & . & . & . \\ D_{N1}^{(0)} & D_{N2}^{(0)} & D_{N3}^{(0)} & D_{N4}^{(0)} \\ \end{matrix} \right] \\ = & \left[ \begin{matrix} g_{2}^{(0)g_{3}^{(0){{T}_{1}}}} & \tfrac{g_{1}^{(0)}}{g_{2}^{(0)}}g_{3}^{(0){{T}_{1}}}g_{2}^{(0)g_{3}^{(0){{T}_{1}}}} & \tfrac{g_{1}^{(0)}}{g_{3}^{(0)}}g_{3}^{(0){{T}_{1}}}\ln (g_{2}^{(0)}){{T}_{1}}g_{2}^{(0)g_{3}^{(0){{T}_{1}}}} & 1 \\ . & . & . & . \\ . & . & . & . \\ g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & \tfrac{g_{1}^{(0)}}{g_{2}^{(0)}}g_{3}^{(0){{T}_{N}}}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & \tfrac{g_{1}^{(0)}}{g_{3}^{(0)}}g_{3}^{(0){{T}_{N}}}\ln (g_{2}^{(0)}){{T}_{N}}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & 1 \\ \end{matrix} \right] \end{align}\,\! }[/math]
- [math]\displaystyle{ {{\nu }^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ g_{4}^{(0)} \\ \end{matrix} \right]\,\! }[/math]
The same reasoning as before is followed here, and the estimate of the parameters [math]\displaystyle{ {{\nu }^{(0)}}\,\! }[/math] is given by:
- [math]\displaystyle{ {{\widehat{\nu }}^{(0)}}={{\left( {{D}^{{{(0)}^{T}}}}{{D}^{(0)}} \right)}^{-1}}{{D}^{{{(0)}^{T}}}}{{Y}^{(0)}}\,\! }[/math]
The revised estimated regression coefficients in matrix form are:
- [math]\displaystyle{ {{g}^{(1)}}={{g}^{(0)}}+{{\widehat{\nu }}^{(0)}}\,\! }[/math]
To see if the revised regression coefficients will lead to a reasonable result, the least squares criterion measure, , should be checked. According to the Least Squares Principle, the solution to the values of the parameters are those values that minimize [math]\displaystyle{ Q\,\! }[/math]. With the starting coefficients, [math]\displaystyle{ {{g}^{(0)}}\,\! }[/math], [math]\displaystyle{ Q\,\! }[/math] is:
- [math]\displaystyle{ {{Q}^{(0)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(0)}}) \right)}^{2}}\,\! }[/math]
With the coefficients at the end of the first iteration, [math]\displaystyle{ {{g}^{(1)}}\,\! }[/math], [math]\displaystyle{ Q\,\! }[/math] is:
- [math]\displaystyle{ {{Q}^{(1)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(1)}}) \right)}^{2}}\,\! }[/math]
For the Gauss-Newton method to work properly, and to satisfy the Least Squares Principle, the relationship [math]\displaystyle{ {{Q}^{(k+1)}}\lt {{Q}^{(k)}}\,\! }[/math] has to hold for all [math]\displaystyle{ k\,\! }[/math], meaning that [math]\displaystyle{ {{g}^{(k+1)}}\,\! }[/math] gives a better estimate than [math]\displaystyle{ {{g}^{(k)}}\,\! }[/math]. The problem is not yet completely solved. Now [math]\displaystyle{ {{g}^{(1)}}\,\! }[/math] are the starting values, producing a new set of values [math]\displaystyle{ {{g}^{(2)}}.\,\! }[/math] The process is continued until the following relationship has been satisfied.
- [math]\displaystyle{ {{Q}^{(s-1)}}-{{Q}^{(s)}}\simeq 0\,\! }[/math]
As mentioned previously, when using the Gauss-Newton method or some other estimation procedure, it is advisable to try several sets of starting values to make sure that the solution gives relatively consistent results. Note that RGA uses a different analysis method called the Levenberg-Marquardt. This method utilizes the best features of the Gauss-Newton method and the method of the steepest descent, and occupies a middle ground between these two methods.
Confidence Bounds
The approximate reliability confidence bounds under the Modified Gompertz model can be obtained using nonlinear regression. Additionally, the reliability is always between 0 and 1. In order to keep the endpoints of the confidence interval, the logit transformation can be used to obtain the confidence bounds on reliability.
- [math]\displaystyle{ CB=\frac{{{{\hat{R}}}_{i}}}{{{{\hat{R}}}_{i}}+(1-{{{\hat{R}}}_{i}}){{e}^{\pm {{z}_{\alpha }}{{{\hat{\sigma }}}_{R}}/\left[ {{{\hat{R}}}_{i}}(1-{{{\hat{R}}}_{i}}) \right]}}}\,\! }[/math]
- [math]\displaystyle{ {{\hat{\sigma }}^{2}}=\frac{SSE}{n-p}\,\! }[/math]
where [math]\displaystyle{ p\,\! }[/math] is the total number of groups (in this case 4) and [math]\displaystyle{ n\,\! }[/math] is the total number of items in each group.
Example: Modified Gompertz for Reliability Data
A reliability growth data set is given in columns 1 and 2 of the following table. Find the Modified Gompertz curve that represents the data and plot it comparatively with the raw data.
| Time(months) | Raw Data Reliability(%) | Gompertz Reliability(%) | Logistic Reliability(%) | Modified Gompertz Reliability(%) |
|---|---|---|---|---|
| 0 | 31.00 | 25.17 | 22.70 | 31.18 |
| 1 | 35.50 | 38.33 | 38.10 | 35.08 |
| 2 | 49.30 | 51.35 | 56.40 | 49.92 |
| 3 | 70.10 | 62.92 | 73.00 | 69.23 |
| 4 | 83.00 | 72.47 | 85.00 | 83.72 |
| 5 | 92.20 | 79.94 | 93.20 | 92.06 |
| 6 | 96.40 | 85.59 | 96.10 | 96.29 |
| 7 | 98.60 | 89.75 | 98.10 | 98.32 |
| 8 | 99.00 | 92.76 | 99.10 | 99.27 |
Solution
To determine the parameters of the Modified Gompertz curve, use:
- [math]\displaystyle{ \begin{align} & {{S}_{1}}(d)= & \underset{i=0}{\overset{2}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ & {{S}_{2}}(d)= & \underset{i=3}{\overset{5}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ & {{S}_{3}}(d)= & \underset{i=6}{\overset{8}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \end{align}\,\! }[/math]
- [math]\displaystyle{ c(d)={{\left[ \frac{{{S}_{3}}(d)-{{S}_{2}}(d)}{{{S}_{2}}(d)-{{S}_{1}}(d)} \right]}^{\tfrac{1}{3}}}\,\! }[/math]
- [math]\displaystyle{ a(d)={{e}^{\left[ \tfrac{1}{3}\left( {{S}_{1}}(d)+\tfrac{{{S}_{2}}(d)-{{S}_{1}}(d)}{1-{{[c(d)]}^{3}}} \right) \right]}}\,\! }[/math]
- [math]\displaystyle{ b(d)={{e}^{\left[ \tfrac{({{S}_{2}}(d)-{{S}_{1}}(d))(c(d)-1)}{{{\left[ 1-{{[c(d)]}^{3}} \right]}^{2}}} \right]}}\,\! }[/math]
- and:
- [math]\displaystyle{ {{R}_{0}}=d+a(d)\cdot b(d)\,\! }[/math]
where [math]\displaystyle{ {{R}_{0}}=31%\,\! }[/math]. Then, Eqn. (eq27) may be rewritten as:
- [math]\displaystyle{ d-31+a(d)\cdot b(d)=0\,\! }[/math]
Eqns. (eq24), (eq25), (eq26) and (eq28) can now be solved simultaneously. One method for solving these equations numerically is to substitute different values of [math]\displaystyle{ d\,\! }[/math], which must be less than [math]\displaystyle{ {{R}_{0}}\,\! }[/math], into Eqn. (eq28) and plot along the y-axis with the value of [math]\displaystyle{ d\,\! }[/math] along the x-axis. The value of [math]\displaystyle{ d\,\! }[/math] can then be read from the x-intercept. This can be repeated for greater accuracy using smaller and smaller increments of [math]\displaystyle{ d\,\! }[/math]. Once the desired accuracy on [math]\displaystyle{ d\,\! }[/math] has been achieved, the value of [math]\displaystyle{ d\,\! }[/math] can then be substituted into Eqns. (eq24), (eq25) and (eq26). Now [math]\displaystyle{ a\,\! }[/math], [math]\displaystyle{ b\,\! }[/math] and [math]\displaystyle{ c\,\! }[/math] can be calculated. For this case, the initial estimates of the parameters are:
- [math]\displaystyle{ \begin{align} \widehat{a}= & 69.324 \\ \widehat{b}= & 0.002524 \\ \widehat{c}= & 0.46012 \\ \widehat{d}= & 30.825 \end{align}\,\! }[/math]
Now, since the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting [math]\displaystyle{ {{Y}_{i}}={{R}_{i}},\,\! }[/math] [math]\displaystyle{ g_{1}^{(0)}=69.324,\,\! }[/math] [math]\displaystyle{ g_{2}^{(0)}=0.002524,\,\! }[/math] [math]\displaystyle{ g_{3}^{(0)}=0.46012,\,\! }[/math] and [math]\displaystyle{ g_{4}^{(0)}=30.825\,\! }[/math], [math]\displaystyle{ {{Y}^{(0)}},{{D}^{(0)}},\,\! }[/math] [math]\displaystyle{ {{\nu }^{(0)}}\,\! }[/math] become:
- [math]\displaystyle{ {{Y}^{(0)}}=\left[ \begin{matrix} 0.000026 \\ 0.253873 \\ -1.062940 \\ 0.565690 \\ -0.845260 \\ 0.096737 \\ 0.076450 \\ 0.238155 \\ -0.320890 \\ \end{matrix} \right]\,\! }[/math]
- [math]\displaystyle{ {{D}^{(0)}}=\left[ \begin{matrix} 0.002524 & 69.3240 & 0.0000 & 1 \\ 0.063775 & 805.962 & -26.4468 & 1 \\ 0.281835 & 1638.82 & -107.552 & 1 \\ 0.558383 & 1493.96 & -147.068 & 1 \\ 0.764818 & 941.536 & -123.582 & 1 \\ 0.883940 & 500.694 & -82.1487 & 1 \\ 0.944818 & 246.246 & -48.4818 & 1 \\ 0.974220 & 116.829 & -26.8352 & 1 \\ 0.988055 & 54.5185 & -14.3117 & 1 \\ \end{matrix} \right]\,\! }[/math]
- [math]\displaystyle{ {{\nu }^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ g_{4}^{(0)} \\ \end{matrix} \right]=\left[ \begin{matrix} 69.324 \\ 0.002524 \\ 0.46012 \\ 30.825 \\ \end{matrix} \right]\,\! }[/math]
The estimate of the parameters [math]\displaystyle{ {{\nu }^{(0)}}\,\! }[/math] is given by:
- [math]\displaystyle{ \begin{align} {{\widehat{\nu }}^{(0)}}= & {{\left( {{D}^{{{(0)}^{T}}}}{{D}^{(0)}} \right)}^{-1}}{{D}^{{{(0)}^{T}}}}{{Y}^{(0)}} \\ = & \left[ \begin{matrix} -0.275569 \\ -0.000549 \\ -0.003202 \\ 0.209458 \\ \end{matrix} \right] \end{align}\,\! }[/math]
The revised estimated regression coefficients in matrix form are given by:
- [math]\displaystyle{ \begin{align} {{g}^{(1)}}= & {{g}^{(0)}}+{{\widehat{\nu }}^{(0)}}. \\ = & \left[ \begin{matrix} 69.324 \\ 0.002524 \\ 0.46012 \\ 30.825 \\ \end{matrix} \right]+\left[ \begin{matrix} -0.275569 \\ -0.000549 \\ -0.003202 \\ 0.209458 \\ \end{matrix} \right] \\ = & \left[ \begin{matrix} 69.0484 \\ 0.00198 \\ 0.45692 \\ 31.0345 \\ \end{matrix} \right] \end{align}\,\! }[/math]
With the starting coefficients [math]\displaystyle{ {{g}^{(0)}}\,\! }[/math], [math]\displaystyle{ Q\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} {{Q}^{(0)}}= & \underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(0)}}) \right)}^{2}} \\ = & 2.403672 \end{align}\,\! }[/math]
With the coefficients at the end of the first iteration, [math]\displaystyle{ {{g}^{(1)}}\,\! }[/math], [math]\displaystyle{ Q\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} {{Q}^{(1)}}= & \underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(1)}} \right) \right]}^{2}} \\ = & 2.073964 \end{align}\,\! }[/math]
Therefore:
- [math]\displaystyle{ \begin{align} {{Q}^{(1)}}\lt {{Q}^{(0)}} \end{align}\,\! }[/math]
Hence, the Gauss-Newton method works in the right direction. The iterations are continued until the relationship of Eqn. (critir) has been satisfied. Using RGA, the estimators of the parameters are:
- [math]\displaystyle{ \begin{align} \widehat{a}= & 0.6904 \\ \widehat{b}= & 0.0020 \\ \widehat{c}= & 0.4567 \\ \widehat{d}= & 0.3104 \end{align}\,\! }[/math]
Therefore, the Modified Gompertz model is:
- [math]\displaystyle{ R=0.3104+(0.6904){{(0.0020)}^{{{0.4567}^{T}}}}\,\! }[/math]
Using Eqn. (eq29), the predicted reliability is plotted in the following figure along with the raw data. It can be seen from the plot in the figure that the Modified Gompertz curve represents the data very well.
More Examples
Standard Gompertz for Grouped per Configuration Data
A new design is put through a reliability growth test. The requirement is that after the ninth stage the design will exhibit an 85% reliability with a 90% confidence level. Given the data in the following table, do the following:
- 1) Estimate the parameters of the Standard Gompertz model.
- 2) What is the initial reliability at [math]\displaystyle{ T=0\,\! }[/math] ?
- 3) Determine the reliability at the end of the ninth stage and check to see if the goal has been met.
| Stage | Number of Units | Number of Failures |
|---|---|---|
| 1 | 10 | 5 |
| 2 | 8 | 3 |
| 3 | 9 | 3 |
| 4 | 9 | 2 |
| 5 | 10 | 2 |
| 6 | 10 | 1 |
| 7 | 10 | 1 |
| 8 | 10 | 1 |
| 9 | 10 | 1 |
Solution
- 1) The data is entered in cumulative format and the estimated Standard Gompertz parameters are shown in the following figure.
- 2) The initial reliability at [math]\displaystyle{ T=0\,\! }[/math] is equal to:
- [math]\displaystyle{ \begin{align} {{R}_{T=0}}= & a\cdot b \\ = & 0.9497\cdot 0.5249 \\ = & 0.4985 \end{align}\,\! }[/math]
- 3) The reliability at the ninth stage can be calculated using the Quick Calculation Pad (QCP) as shown in the figure below.
The estimated reliability at the end of the ninth stage is equal to 91.92%. However, the lower limit at the 90% 1-sided confidence bound is equal to 82.15%. Therefore, the required goal of 85% reliability at a 90% confidence level has not been met.
Comparing Standard and Modified Gompertz
Using the data in the following table, determine whether the Standard Gompertz or Modified Gompertz would be better suited for analyzing the given data.
| Stage | Reliability (%) |
|---|---|
| 0 | 36 |
| 1 | 38 |
| 2 | 46 |
| 3 | 58 |
| 4 | 71 |
| 5 | 80 |
| 6 | 86 |
| 7 | 88 |
| 8 | 90 |
| 9 | 91 |
Solution
The Standard Gompertz Reliability vs. Time plot is shown next.
The Standard Gompertz seems to do a fairly good job of modeling the data. However, it appears that it is having difficulty modeling the S-shape of the data. The Modified Gompertz Reliability vs. Time plot is shown next. As expected, the Modified Gompertz does a much better job of handling the S-shape presented by the data and provides a better fit for this data.