Duane Model: Difference between revisions
| Line 593: | Line 593: | ||
==Duane Confidence Bounds Example== | ==Duane Confidence Bounds Example== | ||
For the data given above in [[Duane_Model#Least_Squares_Example_2|Least Squares Example 2]], calculate the 90% confidence bounds for: | For the data given above in [[Duane_Model#Least_Squares_Example_2|Least Squares Example 2]], calculate the 90% confidence bounds for: | ||
#The parameters <math>\alpha\ | #The parameters <math>\alpha\,\!</math> and <math>b\,\!</math>. | ||
#The cumulative and instantaneous failure intensity. | #The cumulative and instantaneous failure intensity. | ||
#The cumulative and instantaneous MTBF. | #The cumulative and instantaneous MTBF. | ||
'''Solution''' | '''Solution''' | ||
:1. Using the values of <math>\widehat{b}</math> and <math>\widehat{\alpha }</math> estimated from the least squares analysis in Example 3: | :1. Using the values of <math>\widehat{b}\,\!</math> and <math>\widehat{\alpha }\,\!</math> estimated from the least squares analysis in Example 3: | ||
::<math>\widehat{b}=1.9453</math> | ::<math>\widehat{b}=1.9453</math> | ||
::<math>\widehat{\alpha}=0.6133 | ::<math>\widehat{\alpha}=0.6133 | ||
Eqn. (duanec9) is: | Eqn. (duanec9) is: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{S}_{xx}}= & 1400.9084-1301.4545 \\ | & {{S}_{xx}}= & 1400.9084-1301.4545 \\ | ||
& = & 99.4539 | & = & 99.4539 | ||
\end{align}</math> | \end{align}</math> | ||
Eqn. (duanec7) is: | Eqn. (duanec7) is: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& SE(\hat{\alpha })= & \frac{\sigma }{\sqrt{{{S}_{xx}}}} \\ | & SE(\hat{\alpha })= & \frac{\sigma }{\sqrt{{{S}_{xx}}}} \\ | ||
| Line 626: | Line 619: | ||
\end{align}</math> | \end{align}</math> | ||
Eqn. (duanec8) is: | Eqn. (duanec8) is: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& SE(\ln \hat{b})= & \sigma \cdot \sqrt{\frac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{(\ln {{T}_{i}})}^{2}}}{n\cdot {{S}_{xx}}}} \\ | & SE(\ln \hat{b})= & \sigma \cdot \sqrt{\frac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{(\ln {{T}_{i}})}^{2}}}{n\cdot {{S}_{xx}}}} \\ | ||
| Line 635: | Line 626: | ||
\end{align}</math> | \end{align}</math> | ||
Thus, 90% confidence bounds on parameter <math>\alpha </math> using Eqn. (duanec1) are: | Thus, 90% confidence bounds on parameter <math>\alpha \,\!</math> using Eqn. (duanec1) are: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{\alpha }_{L}}= & 0.602050 \\ | & {{\alpha }_{L}}= & 0.602050 \\ | ||
| Line 643: | Line 633: | ||
\end{align}</math> | \end{align}</math> | ||
And 90% confidence bounds on parameter <math>b\,\!</math> using Eqn. (duanec2) are: | |||
And 90% confidence bounds on parameter <math>b</math> using Eqn. (duanec2) are: | |||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{b}_{L}}= & 1.7831 \\ | & {{b}_{L}}= & 1.7831 \\ | ||
| Line 653: | Line 640: | ||
\end{align}</math> | \end{align}</math> | ||
:2. The cumulative failure intensity is: | :2. The cumulative failure intensity is: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{\lambda }_{c}}= & \frac{1}{1.9453}\cdot {{22000}^{-0.6133}} \\ | & {{\lambda }_{c}}= & \frac{1}{1.9453}\cdot {{22000}^{-0.6133}} \\ | ||
| Line 662: | Line 647: | ||
\end{align}</math> | \end{align}</math> | ||
And the instantaneous failure intensity is equal to: | And the instantaneous failure intensity is equal to: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{\lambda }_{i}}= & \frac{1}{1.9453}\cdot (1-0.6133)\cdot {{22000}^{-0.6133}} \\ | & {{\lambda }_{i}}= & \frac{1}{1.9453}\cdot (1-0.6133)\cdot {{22000}^{-0.6133}} \\ | ||
| Line 671: | Line 654: | ||
\end{align}</math> | \end{align}</math> | ||
So, at the 90% confidence level and for <math>T=22,000\,\!</math> hr, the confidence bounds on cumulative failure intensity are: | |||
So, at the 90% confidence level and for <math>T=22,000</math> hr, the confidence bounds on cumulative failure intensity are: | |||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{[{{\lambda }_{c}}(t)]}_{L}}= & 0.00100254 \\ | & {{[{{\lambda }_{c}}(t)]}_{L}}= & 0.00100254 \\ | ||
| Line 680: | Line 661: | ||
\end{align}</math> | \end{align}</math> | ||
For the instantaneous failure intensity: | For the instantaneous failure intensity: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{[{{\lambda }_{i}}(t)]}_{L}}= & 0.00038775 \\ | & {{[{{\lambda }_{i}}(t)]}_{L}}= & 0.00038775 \\ | ||
| Line 689: | Line 668: | ||
\end{align}</math> | \end{align}</math> | ||
Figures figure75 and figure76 show the graphs of the cumulative and instantaneous failure intensity. Both are plotted with confidence bounds. | Figures figure75 and figure76 show the graphs of the cumulative and instantaneous failure intensity. Both are plotted with confidence bounds. | ||
[[Image:rga4.7.png|thumb|center|400px|Cumulative Failure Intensity plot with 2-sided 90% confidence bounds.]] | [[Image:rga4.7.png|thumb|center|400px|Cumulative Failure Intensity plot with 2-sided 90% confidence bounds.]] | ||
[[Image:rga4.8.png|thumb|center|400px|Instantaneous Failure Intensity plot with 2-sided 90% confidence bounds.]] | [[Image:rga4.8.png|thumb|center|400px|Instantaneous Failure Intensity plot with 2-sided 90% confidence bounds.]] | ||
:3. The cumulative MTBF is: | :3. The cumulative MTBF is: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{m}_{c}}(T)= & 1.9453\cdot {{22000}^{0.6133}} \\ | & {{m}_{c}}(T)= & 1.9453\cdot {{22000}^{0.6133}} \\ | ||
| Line 707: | Line 682: | ||
\end{align}</math> | \end{align}</math> | ||
And the instantaneous MTBF is: | And the instantaneous MTBF is: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{m}_{i}}(T)= & \frac{1.9453}{1-0.6133}\cdot {{22000}^{0.6133}} \\ | & {{m}_{i}}(T)= & \frac{1.9453}{1-0.6133}\cdot {{22000}^{0.6133}} \\ | ||
| Line 716: | Line 689: | ||
\end{align}</math> | \end{align}</math> | ||
So, at 90% confidence level and for <math>T=22,000\,\!</math> hr, the confidence bounds on the cumulative MTBF are: | |||
So, at 90% confidence level and for <math>T=22,000</math> hr, the confidence bounds on the cumulative MTBF are: | |||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{m}_{c}}{{(t)}_{l}}= & 803.6695 \\ | & {{m}_{c}}{{(t)}_{l}}= & 803.6695 \\ | ||
| Line 725: | Line 696: | ||
\end{align}</math> | \end{align}</math> | ||
The confidence bounds for the instantaneous MTBF are: | The confidence bounds for the instantaneous MTBF are: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& {{m}_{i}}{{(t)}_{l}}= & 2077.9204 \\ | & {{m}_{i}}{{(t)}_{l}}= & 2077.9204 \\ | ||
| Line 734: | Line 703: | ||
\end{align}</math> | \end{align}</math> | ||
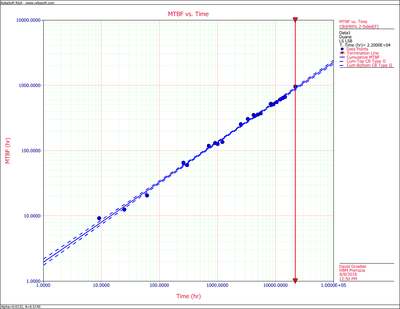
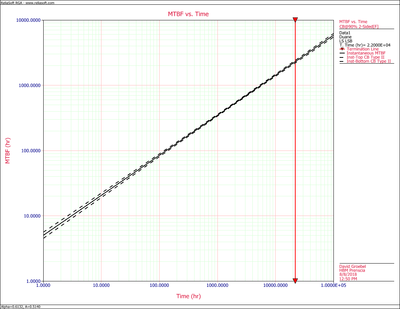
Figure CumMTBFCB displays the cumulative MTBF while Figure InstMTBFCB displays the instantaneous MTBF. Both are plotted with confidence bounds. | Figure CumMTBFCB displays the cumulative MTBF while Figure InstMTBFCB displays the instantaneous MTBF. Both are plotted with confidence bounds. | ||
[[Image:rga4.9.png|thumb|center|400px|Cumulative MTBF plot with 2-sided 90% condfidence bounds.]] | [[Image:rga4.9.png|thumb|center|400px|Cumulative MTBF plot with 2-sided 90% condfidence bounds.]] | ||
[[Image:rga4.10.png|thumb|center|400px|Instantaneous MTBF plot with 2-sided 90% confidence bounds.]] | [[Image:rga4.10.png|thumb|center|400px|Instantaneous MTBF plot with 2-sided 90% confidence bounds.]] | ||
=More Examples= | =More Examples= | ||
Revision as of 00:17, 28 August 2012
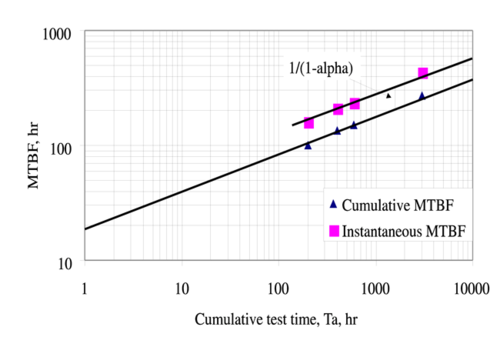
In 1962, J. T. Duane published a report in which he presented failure data of different systems during their development programs [8]. While analyzing the data, it was observed that the cumulative MTBF versus cumulative operating time followed a straight line when plotted on log-log paper, as shown next.
Based on that observation, Duane developed his model as follows. If [math]\displaystyle{ N(T)\,\! }[/math] is the number of failures by time [math]\displaystyle{ T\,\! }[/math] , the observed mean (average) time between failures, [math]\displaystyle{ MTB{{F}_{c}},\,\! }[/math] at time [math]\displaystyle{ T\,\! }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{T}{N(T)} }[/math]
The equation of the line can be expressed as:
- [math]\displaystyle{ \begin{align} y=mx+c \end{align} }[/math]
Setting:
- [math]\displaystyle{ \begin{align} y= & \ln (MTB{{F}_{c}}) \\ x= & \ln (T) \\ m= & \alpha \\ c= & \ln b \end{align} }[/math]
yields:
- [math]\displaystyle{ \begin{align} \ln (MTB{{F}_{c}})=\ln b+\alpha \ln (T) \end{align} }[/math]
Then equating [math]\displaystyle{ MTB{{F}_{c}}\,\! }[/math] to its expected value, and assuming an exact linear relationship, gives:
- [math]\displaystyle{ \begin{align} E(MTB{{F}_{c}})=b{{T}^{\alpha }} \end{align} }[/math]
or:
- [math]\displaystyle{ \begin{align} MTB{{F}_{c}}=b{{T}^{\alpha }} \end{align} }[/math]
And, if you assume a constant failure intensity, then the cumulative failure intensity, [math]\displaystyle{ {{\lambda }_{c}}\,\! }[/math] , is:
- [math]\displaystyle{ E({{\lambda }_{c}})=\frac{1}{b}{{T}^{-\alpha }} }[/math]
or:
- [math]\displaystyle{ {{\widehat{{\bar{\lambda }}}}_{c}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Also, the expected number of failures up to time [math]\displaystyle{ T\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} & E(N(T))= & {{\widehat{{\bar{\lambda }}}}_{c}}\cdot T \\ & = & \frac{1}{b}{{T}^{1-\alpha }} \end{align} }[/math]
where:
- [math]\displaystyle{ \begin{align} {{\widehat{{\bar{\lambda }}}}_{c}}= & \text{the average estimate of the cumulative failure intensity, failures/hr}\text{.} \\ T= & \text{the total accumulated unit hours of test and/or development time}\text{.} \\ 1/b= & \text{the cumulative failure intensity at }T=1\text{, or at the beginning of the test,} \\ & \text{or the earliest time at which the first }\widehat{{\bar{\lambda }}}\text{ is predicted, or the }\widehat{{\bar{\lambda }}}\text{ for the} \\ & \text{equipment at the start of the design and development process}\text{.} \\ \alpha = & \text{the improvement rate in the }\widehat{{\bar{\lambda }}}\text{, }0\le \alpha \le 1. \end{align} }[/math]
The corresponding [math]\displaystyle{ MTB{{F}_{c}}\,\! }[/math] , or [math]\displaystyle{ {{\hat{m}}_{c}}\,\! }[/math] , is equal to:
- [math]\displaystyle{ {{\hat{m}}_{c}}=b{{T}^{\alpha }} }[/math]
where [math]\displaystyle{ b=\,\! }[/math] cumulative MTBF at [math]\displaystyle{ T=1 }[/math] or at the beginning of the test, or the earliest time at which the first [math]\displaystyle{ \hat{m}\,\! }[/math] can be determined, or the [math]\displaystyle{ \hat{m}\,\! }[/math] predicted at the start of the design and development process ( [math]\displaystyle{ b\gt 0\,\! }[/math] ). The cumulative MTBF, [math]\displaystyle{ {{\hat{m}}_{c}}\,\! }[/math] , and [math]\displaystyle{ {{\widehat{{\bar{\lambda }}}}_{c}}\,\! }[/math] tell whether [math]\displaystyle{ m\,\! }[/math] is increasing or [math]\displaystyle{ \lambda \,\! }[/math] is decreasing with time, utilizing all data up to that time. You may want to know, however, the instantaneous [math]\displaystyle{ {{\hat{m}}_{i}}\,\! }[/math] or [math]\displaystyle{ {{\widehat{{\bar{\lambda }}}}_{i}}\,\! }[/math] to see what you are doing at a specific instant or after a specific test and development time. The instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}\,\! }[/math] , is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{i}}= & \frac{d(E(N(T)))}{dT} \\ & = & \frac{1}{b}(1-\alpha ){{T}^{-\alpha }} \\ & = & (1-\alpha ){{\lambda }_{c}} \end{align} }[/math]
Similarly, using Eqn. (duanecnew), this procedure yields:
- [math]\displaystyle{ \begin{align} & {{m}_{i}}= & \frac{1}{1-\alpha }b{{T}^{\alpha }} \\ & = & \frac{1}{1-\alpha }{{{\hat{m}}}_{c}},:\ \ \alpha \not{=}1 \end{align} }[/math]
where [math]\displaystyle{ \alpha =1\,\! }[/math] implies infinite MTBF growth. It can be seen from Eqn. (duane0) that the instantaneous failure intensity improvement line is obtained by shifting the cumulative failure intensity line down, parallel to itself, by a distance of [math]\displaystyle{ (1-\alpha )\,\! }[/math] . Similarly, it can be seen from Eqn. (eq76) that the current or instantaneous MTBF growth line is obtained by shifting the cumulative MTBF line up, parallel to itself, by a distance of [math]\displaystyle{ \tfrac{1}{1-\alpha }\,\! }[/math] , as illustrated in the figure below.
Parameter Estimation
The Duane model is a two parameter model. Therefore, to use this model as a basis for predicting the reliability growth that could be expected in an equipment development program, procedures must be defined for estimating these parameters as a function of equipment characteristics. Note that, while these parameters can be estimated for a given data set using curve-fitting methods, there exists no underlying theory for the Duane model that could provide a basis for a priori estimation.
Graphical Method
Eqn. (duaneb) may be linearized by taking the natural log of both sides:
- [math]\displaystyle{ \ln \left( {{\widehat{{\bar{\lambda }}}}_{c}} \right)=\ln \left( \frac{1}{b} \right)-\alpha \ln (T) }[/math]
Consequently, plotting [math]\displaystyle{ \widehat{{\bar{\lambda }}}\,\! }[/math] versus [math]\displaystyle{ T\,\! }[/math] on log-log paper will result in a straight line with a negative slope, such that:
- [math]\displaystyle{ \begin{align} ln({\frac{1}{b}})=& \text{the y-intercept at T}=1 \\ \frac{1}{b}=& \text{the cumulative failure intensity at T}=1 \\ \alpha=& \text{the slope of the straight line on the log-log plot} \end{align} }[/math]
Similarly, Eqn. (duane6) can also be linearized by taking the natural log of both sides:
- [math]\displaystyle{ \begin{align} \ln {{\hat{m}}_{c}} = \ln b+\alpha \ln T \end{align} }[/math]
Plotting [math]\displaystyle{ \hat{m} }[/math] versus [math]\displaystyle{ T\,\! }[/math] on log-log paper will result in a straight line with a positive slope such that:
- [math]\displaystyle{ \begin{align} \ln{b}=& \text{the y-intercept at T}=1 \\ b=& \text{the cumulative mean time between failure at T}=1 \\ \alpha=& \text{the slope of the straight line on the log-log plot} \end{align} }[/math]
Two ways of determining these curves are as follows:
- 1. Predict the [math]\displaystyle{ {{\widehat{{\bar{\lambda }}}}_{0}} }[/math] and [math]\displaystyle{ \hat{m}=\,\! }[/math] [math]\displaystyle{ \tfrac{1}{{{\widehat{{\bar{\lambda }}}}_{0}}}\,\! }[/math] of the system from its reliability block diagram and available component failure intensities. Plot this value on log-log plotting paper at [math]\displaystyle{ T=1.\,\! }[/math] From past experience and from past data for similar equipment, find values of [math]\displaystyle{ {{\alpha }_{1}}\,\! }[/math] , the slope of the improvement lines for [math]\displaystyle{ \widehat{{\bar{\lambda }}}\,\! }[/math] or [math]\displaystyle{ \hat{m}\,\! }[/math] . Modify this [math]\displaystyle{ \alpha }[/math] as necessary. If a better design effort is expected and a more intensive research, test and development or TAAF program is to be implemented, then a [math]\displaystyle{ 15% }[/math] improvement in the growth rate may be attainable. Consequently, the available value for slope [math]\displaystyle{ \alpha \,\! }[/math] , and [math]\displaystyle{ {{\alpha }_{1}}\,\! }[/math] , should be adjusted by this amount. The value to be used will then be [math]\displaystyle{ \alpha =1.15{{\alpha }_{1}}.\,\! }[/math] A line is then drawn through point [math]\displaystyle{ {{\widehat{{\bar{\lambda }}}}_{0}}\,\! }[/math] and [math]\displaystyle{ T=1\,\! }[/math] with the just determined slope [math]\displaystyle{ \alpha \,\! }[/math] , keeping in mind that [math]\displaystyle{ \alpha \,\! }[/math] is negative for the [math]\displaystyle{ \widehat{{\bar{\lambda }}}\,\! }[/math] curve. This line should be extended to the design, development and test time scheduled to be expended to see if the failure intensity goal will indeed be achieved on schedule. It is also possible to find that the design, development and test time to achieve the goal may be earlier than the delivery date or later. If earlier, then either the reliability program effort can be judiciously and appropriately trimmed; or if it is an incentive contract, full advantage is taken of the fact that the failure intensity goal can be exceeded with the associated increased profits to the company. A similar approach may be used for the MTBF growth model, where [math]\displaystyle{ {{\hat{m}}_{0}}=\tfrac{1}{{{\widehat{{\bar{\lambda }}}}_{0}}}\,\! }[/math] is plotted at [math]\displaystyle{ T=1\,\! }[/math] , and a line is drawn through the point [math]\displaystyle{ {{\hat{m}}_{0}}\,\! }[/math] and [math]\displaystyle{ T=1\,\! }[/math] with slope [math]\displaystyle{ \alpha \,\! }[/math] to obtain the MTBF growth line. If [math]\displaystyle{ \alpha }[/math] values are not available, consult the table below, which gives actual [math]\displaystyle{ \alpha \,\! }[/math] values for various types of equipment. These have been obtained from the literature or by MTBF growth tests. It may be seen from the following table that [math]\displaystyle{ \alpha \,\! }[/math] values range between 0.24 and 0.65. The lower values reflect slow early growth and the higher values reflect fast early growth.
| Equipment | Slope([math]\displaystyle{ \alpha }[/math]) | |
|---|---|---|
| Computer system | Actual | 0.24 |
| Easy to find failures were eliminated | 0.26 | |
| All known failure causes were eliminated | 0.36 | |
| Mainframe computer | 0.50 | |
| Aerospace electronics | All malfunctions | 0.57 |
| Relevant failures only | 0.65 | |
| Attack radar | 0.60 | |
| Rocket engine | 0.46 | |
| Afterburning turbojet | 0.35 | |
| Complex hydromechanical system | 0.60 | |
| Aircraft generator | 0.38 | |
| Modern dry turbojet | 0.48 |
- 2. During the design, development and test phase and at specific milestones, the [math]\displaystyle{ \widehat{{\bar{\lambda }}}=\tfrac{1}{{\hat{m}}}\,\! }[/math] is calculated from the total failures and [math]\displaystyle{ T\,\! }[/math] values. These values of [math]\displaystyle{ \widehat{{\bar{\lambda }}}\,\! }[/math] or [math]\displaystyle{ \hat{m}\,\! }[/math] are plotted above the corresponding [math]\displaystyle{ T\,\! }[/math] values on log-log paper. A straight line is drawn favoring these points to minimize the distance between the points and the line, thus establishing the improvement or growth model and its parameters graphically. If needed, linear regression analysis techniques can be used to determine these parameters.
Graphical Method Example
A complex system's reliability growth is being monitored and the data set is given in the table below.
| Point Number | Cumulative Test Time(hr) | Cumulative Failures | Cumulative MTBF(hr) | Instantaneous MTBF(hr) |
|---|---|---|---|---|
| 1 | 200 | 2 | 100.0 | 100 |
| 2 | 400 | 3 | 133.0 | 200 |
| 3 | 600 | 4 | 150.0 | 200 |
| 4 | 3,000 | 11 | 273.0 | 342.8 |
Do the following:
- 1) Plot the cumulative MTBF growth curve.
- 2) Write the equation of this growth curve.
- 3) Write the equation of the instantaneous MTBF growth model.
- 4) Plot the instantaneous MTBF growth curve.
Solution
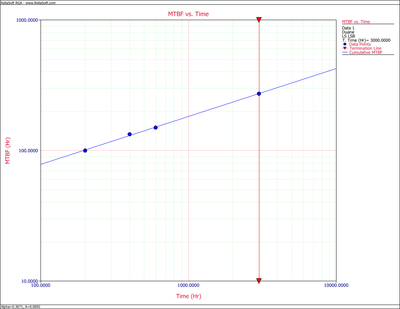
- 1) Given the data in the second and third columns of the above table, the cumulative MTBF, [math]\displaystyle{ {{\hat{m}}_{c}}\,\! }[/math] , values are calculated in the fourth column. The information in the second and fourth columns is then plotted. The first figure below shows the cumulative MTBF while the second figure below shows the instantaneous MTBF. It can be seen that a straight line represents the MTBF growth very well on log-log scales.
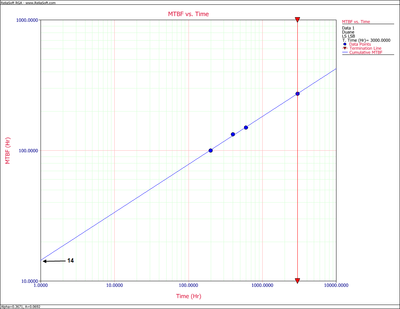
By changing the x-axis scaling, you are able to extend the line to [math]\displaystyle{ T=1\,\! }[/math] . You can get the value of [math]\displaystyle{ b\,\! }[/math] from the graph by positioning the cursor at the point where the line meets the y-axis. Then read the value of the y-coordinate position at the bottom left corner. In this case, [math]\displaystyle{ b\,\! }[/math] is approximately 14 hr. The next figure illustrates this.
Another way of determining [math]\displaystyle{ b }[/math] is to calculate [math]\displaystyle{ \alpha }[/math] by using two points on the fitted straight line and substituting the corresponding [math]\displaystyle{ {{\hat{m}}_{c}}\,\! }[/math] and [math]\displaystyle{ T\,\! }[/math] values into:
- [math]\displaystyle{ \alpha =\frac{\ln \left( {{{\hat{m}}}_{{{c}_{2}}}} \right)-\ln \left( {{{\hat{m}}}_{{{c}_{1}}}} \right)}{\ln \left( {{T}_{_{2}}} \right)-\ln \left( {{T}_{_{1}}} \right)} }[/math]
Then substitute this [math]\displaystyle{ \alpha \,\! }[/math] and choose a set of values for [math]\displaystyle{ {{\hat{m}}_{{{c}_{1}}}}\,\! }[/math] and [math]\displaystyle{ {{T}_{_{1}}}\,\! }[/math] into Eqn. (duane6) and solve for [math]\displaystyle{ b\,\! }[/math] . The slope of the line, [math]\displaystyle{ \alpha \,\! }[/math] , may also be found from Eqn. (eq73) or from:
- [math]\displaystyle{ \alpha =\frac{\ln \left( {{{\hat{m}}}_{c}} \right)-\ln (b)}{\ln (T)-\ln (1)} }[/math]
Using the plot in Figure figold72, at [math]\displaystyle{ {{T}_{_{1}}}=200\,\! }[/math] hr, [math]\displaystyle{ {{\hat{m}}_{{{c}_{1}}}}=100\,\! }[/math] hr. At [math]\displaystyle{ {{T}_{_{2}}}=3,500\,\! }[/math] hr, [math]\displaystyle{ {{\hat{m}}_{{{c}_{2}}}}=300\,\! }[/math] hr. From Figure figold73, at [math]\displaystyle{ b=14\,\! }[/math] hr when [math]\displaystyle{ T=1\,\! }[/math].
Substituting the first set of values, [math]\displaystyle{ b=14\,\! }[/math] hr and [math]\displaystyle{ \ln 1=0\,\! }[/math] , into Eqn. (eq77) yields:
- [math]\displaystyle{ \begin{align} & {{\alpha }_{1}}= & \frac{\ln (100)-\ln (14)}{\ln (200)-\ln (1)} \\ & = & 0.3711 \end{align} }[/math]
- 2. Substituting the second set of values, [math]\displaystyle{ b=14\,\! }[/math] hr and [math]\displaystyle{ \ln 1=0,\,\! }[/math] into Eqn. (eq77) yields:
- [math]\displaystyle{ \begin{align} & {{\alpha }_{2}}= & \frac{\ln (300)-\ln (14)}{\ln (3,500)-\ln (1)} \\ & = & 0.3755 \end{align} }[/math]
Averaging these two [math]\displaystyle{ \alpha \,\! }[/math] values yields a better estimate of [math]\displaystyle{ \widehat{\alpha }=0.3733\,\! }[/math].
- 3. Now the equation for the cumulative MTBF growth curve is:
- [math]\displaystyle{ {{\hat{m}}_{c}}=14\cdot {{T}^{\text{ }0.3733}} }[/math]
- 4. The equation for the instantaneous MTBF growth curve using Eqn. (eq76) is:
- [math]\displaystyle{ \begin{align} {{\hat{m}}_{i}}=\frac{1}{1-0.3733} \cdot {{14T}^{0.3733}} \end{align} }[/math]
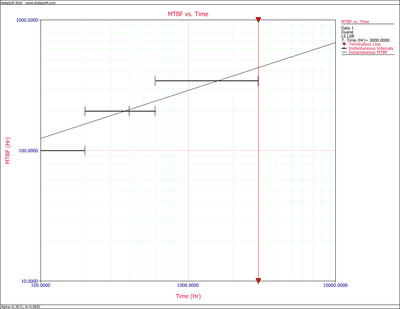
Eqn. (eq80) is plotted in Figures figold72a and figold72b. In Figure figold72b, you can see that a parallel shift upward of the cumulative MTBF, [math]\displaystyle{ {{\hat{m}}_{c}}\,\! }[/math] , line by a distance of [math]\displaystyle{ \tfrac{1}{1-\alpha }\,\! }[/math] gives the instantaneous MTBF, or the [math]\displaystyle{ {{\hat{m}}_{i}}\,\! }[/math] , line.
Least Squares (Linear Regression)
The parameters can also be estimated using a mathematical approach. To do this, apply least squares analysis on Eqn. (eq73):
- [math]\displaystyle{ \ln ({{\hat{m}}_{c}})=\ln (b)+\alpha \ln (T) }[/math]
And for simplicity in the calculations, let:
- [math]\displaystyle{ \begin{align} \ln ({{m}_{ci}})= & {{Y}_{i}} \\ \ln (b)= & a \\ \alpha = & c \\ \ln ({{T}_{i}})= & {{X}_{i}} \end{align} }[/math]
Therefore, Eqn. (mc) becomes:
- [math]\displaystyle{ {{Y}_{i}}=\widehat{a}+\widehat{c}{{X}_{i}} }[/math]
Assume that a set of data pairs [math]\displaystyle{ ({{X}_{1}},{{Y}_{1}})\,\! }[/math] , [math]\displaystyle{ ({{X}_{2}},{{Y}_{2}})\,\! }[/math] ,..., [math]\displaystyle{ ({{X}_{N}},{{Y}_{N}})\,\! }[/math] were obtained and plotted. Then according to the Least Squares Principle, which minimizes the vertical distance between the data points and the straight line fitted to the data, the best fitting straight line to this data set is the straight line [math]\displaystyle{ Y=\widehat{a}+\widehat{c}X\,\! }[/math] such that:
- [math]\displaystyle{ \underset{i=1}{\overset{N}{\mathop \sum }}\,{{(\widehat{a}+\widehat{c}{{X}_{i}}-{{Y}_{i}})}^{2}}=\underset{(a,c)}{\mathop{min}}\,\underset{i=1}{\overset{N}{\mathop \sum }}\,{{(a+c{{X}_{i}}-{{Y}_{i}})}^{2}} }[/math]
And where [math]\displaystyle{ \widehat{a}\,\! }[/math] and [math]\displaystyle{ \widehat{c}\,\! }[/math] are the least squares estimates of [math]\displaystyle{ a\,\! }[/math] and [math]\displaystyle{ c\,\! }[/math] . To obtain [math]\displaystyle{ \widehat{a}\,\! }[/math] and [math]\displaystyle{ \widehat{c}\,\! }[/math] , let:
- [math]\displaystyle{ F=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{(a+c{{X}_{i}}-{{Y}_{i}})}^{2}} }[/math]
Differentiating [math]\displaystyle{ F\,\! }[/math] with respect to [math]\displaystyle{ a\,\! }[/math] and [math]\displaystyle{ c\,\! }[/math] yields:
- [math]\displaystyle{ \frac{\partial F}{\partial a}=2\underset{i=1}{\overset{N}{\mathop \sum }}\,(a+c{{X}_{i}}-{{Y}_{i}}) }[/math]
- and:
- [math]\displaystyle{ \frac{\partial F}{\partial c}=2\underset{i=1}{\overset{N}{\mathop \sum }}\,(a+c{{X}_{i}}-{{Y}_{i}}){{X}_{i}} }[/math]
Set Eqns. (ls2) and (ls3) equal to zero:
- [math]\displaystyle{ \underset{i=1}{\overset{N}{\mathop \sum }}\,(a+c{{X}_{i}}-{{Y}_{i}})=\underset{i=1}{\overset{N}{\mathop \sum }}\,(\widehat{{{Y}_{i}}}-{{Y}_{i}})=-\underset{i=1}{\overset{N}{\mathop \sum }}\,({{Y}_{i}}-\widehat{{{Y}_{i}}})=0 }[/math]
- and:
- [math]\displaystyle{ \underset{i=1}{\overset{N}{\mathop \sum }}\,(a+c{{X}_{i}}-{{Y}_{i}}){{X}_{i}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,(\widehat{{{Y}_{i}}}-{{Y}_{i}}){{X}_{i}}=-\underset{i=1}{\overset{N}{\mathop \sum }}\,({{Y}_{i}}-\widehat{{{Y}_{i}}}){{X}_{i}}=0 }[/math]
Solve the equations simultaneously:
- and:
- [math]\displaystyle{ \widehat{c}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{X}_{i}}{{Y}_{i}}-\tfrac{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{X}_{i}}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{Y}_{i}} \right)}{N}}{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,X_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{X}_{i}} \right)}^{2}}}{N}} }[/math]
Now substituting back [math]\displaystyle{ \ln ({{m}_{ci}})={{Y}_{i}},\,\! }[/math] [math]\displaystyle{ \ln (b)=a,\,\! }[/math] [math]\displaystyle{ \alpha =c\,\! }[/math] and [math]\displaystyle{ \ln ({{T}_{i}})={{X}_{i}},\,\! }[/math] we have:
- [math]\displaystyle{ \widehat{b}={{e}^{\tfrac{1}{n}\left[ \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{m}_{ci}})-\alpha \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}}) \right]}} }[/math]
- where:
- [math]\displaystyle{ \widehat{\alpha }=\frac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}})\ln ({{m}_{ci}})-\tfrac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}})\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{m}_{ci}})}{n}}{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{\left[ \ln ({{T}_{i}}) \right]}^{2}}-\tfrac{{{\left( \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}}) \right)}^{2}}}{n}} }[/math]
Least Squares Example 1
Using the data from the Graphical Method Example given above, estimate the parameters of the MTBF model using least squares.
Solution
From the data table:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{n}{\mathop \sum }}\,\ln ({{T}_{i}})= & 25.693 \\ & \underset{i=1}{\overset{n}{\mathop \sum }}\,\ln ({{T}_{i}})\ln ({{m}_{ci}})= & 130.66 \\ & \underset{i=1}{\overset{n}{\mathop \sum }}\,\ln ({{m}_{ci}})= & 20.116 \\ & \underset{i=1}{\overset{n}{\mathop \sum }}\,{{\left[ \ln ({{T}_{i}}) \right]}^{2}}= & 168.99 \end{align} }[/math]
From Eqn. (Dalpha):
- [math]\displaystyle{ \begin{align} & \widehat{\alpha }= & \frac{130.66-\tfrac{25.693\cdot 20.116}{4}}{168.99-\tfrac{{{25.693}^{2}}}{4}} \\ & = & 0.3671 \end{align} }[/math]
Also from Eqn. (Dbi):
- [math]\displaystyle{ \begin{align} & \widehat{b}= & {{e}^{\tfrac{1}{4}(20.116-0.3671\cdot 25.693)}} \\ & = & 14.456 \end{align} }[/math]
Therefore, Eqn. (duane6) becomes:
- [math]\displaystyle{ {{\hat{m}}_{c}}=14.456\cdot {{T}^{0.3671}} }[/math]
The equation for the instantaneous MTBF growth curve using Eqn. (eq76) is:
- [math]\displaystyle{ {{\hat{m}}_{i}}=\frac{1}{1-0.3671}(14.456){{T}^{0.3671}} }[/math]
Least Squares Example 2
For the data given in columns 1 and 2 of the following table, estimate the Duane parameters using least squares.
| (1)Failure Number | (2)Failure Time(hr) | (3)[math]\displaystyle{ \ln{T_i}\,\! }[/math] | (4)[math]\displaystyle{ \ln{T_i}^2\,\! }[/math] | (5)[math]\displaystyle{ m_c\,\! }[/math] | (6)[math]\displaystyle{ \ln{m_c}\,\! }[/math] | (7)[math]\displaystyle{ \ln{m_c}\cdot\ln{T_i}\,\! }[/math] |
|---|---|---|---|---|---|---|
| 1 | 9.2 | 2.219 | 4.925 | 9.200 | 2.219 | 4.925 |
| 2 | 25 | 3.219 | 10.361 | 12.500 | 2.526 | 8.130 |
| 3 | 61.5 | 4.119 | 16.966 | 20.500 | 3.020 | 12.441 |
| 4 | 260 | 5.561 | 30.921 | 65.000 | 4.174 | 23.212 |
| 5 | 300 | 5.704 | 32.533 | 60.000 | 4.094 | 23.353 |
| 6 | 710 | 6.565 | 43.103 | 118.333 | 4.774 | 31.339 |
| 7 | 916 | 6.820 | 46.513 | 130.857 | 4.874 | 33.241 |
| 8 | 1010 | 6.918 | 47.855 | 126.250 | 4.838 | 33.470 |
| 9 | 1220 | 7.107 | 50.504 | 135.556 | 4.909 | 34.889 |
| 10 | 2530 | 7.836 | 61.402 | 253.000 | 5.533 | 43.359 |
| 11 | 3350 | 8.117 | 65.881 | 304.545 | 5.719 | 46.418 |
| 12 | 4200 | 8.343 | 69.603 | 350.000 | 5.858 | 48.872 |
| 13 | 4410 | 8.392 | 70.419 | 339.231 | 5.827 | 48.895 |
| 14 | 4990 | 8.515 | 72.508 | 356.429 | 5.876 | 50.036 |
| 15 | 5570 | 8.625 | 74.393 | 371.333 | 5.917 | 51.036 |
| 16 | 8310 | 9.025 | 81.455 | 519.375 | 6.253 | 56.431 |
| 17 | 8530 | 9.051 | 81.927 | 501.765 | 6.218 | 56.282 |
| 18 | 9200 | 9.127 | 83.301 | 511.111 | 6.237 | 56.921 |
| 19 | 10500 | 9.259 | 85.731 | 552.632 | 6.315 | 58.469 |
| 20 | 12100 | 9.401 | 88.378 | 605.000 | 6.405 | 60.215 |
| 21 | 13400 | 9.503 | 90.307 | 638.095 | 6.458 | 61.375 |
| 22 | 14600 | 9.589 | 91.945 | 663.636 | 6.498 | 62.305 |
| 23 | 22000 | 9.999 | 99.976 | 956.522 | 6.863 | 68.625 |
| [math]\displaystyle{ \color{Blue}Sum = }[/math] | [math]\displaystyle{ \color{Blue}173.013 }[/math] | [math]\displaystyle{ \color{Blue}1400.908 }[/math] | [math]\displaystyle{ \color{Blue}7600.870 }[/math] | [math]\displaystyle{ \color{Blue}121.406 }[/math] | [math]\displaystyle{ \color{Blue}974.242 }[/math] |
Solution
To estimate the parameters using least squares, the values in columns 3, 4, 5, 6 and 7 are calculated. The cumulative MTBF, [math]\displaystyle{ {{m}_{c}}\,\! }[/math] , is calculated by dividing the failure time by the failure number. From Eqn. (Dalpha), [math]\displaystyle{ \widehat{\alpha }\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\alpha }= & \frac{974.242-\tfrac{173.013\cdot 121.406}{23}}{1400.908-\tfrac{{{(173.013)}^{2}}}{23}} \\ & = & 0.6133 \end{align} }[/math]
The estimator of [math]\displaystyle{ b\,\! }[/math] can be estimated from Eqn. (Dbi):
- [math]\displaystyle{ \begin{align} & \widehat{b}= & {{e}^{\tfrac{1}{23}(121.406-0.6133\cdot 173.013)}} \\ & = & 1.9453 \end{align} }[/math]
Therefore, Eqn. (duane6) becomes:
- [math]\displaystyle{ {{\hat{m}}_{c}}=1.9453\cdot {{T}^{0.613}} }[/math]
Using Eqn. (eq76), the equation for the instantaneous MTBF growth curve is:
- [math]\displaystyle{ {{\hat{m}}_{i}}=\frac{1}{1-0.613}(1.945){{T}^{0.613}} }[/math]
Least Squares Example 3
For the data given in the following table, estimate the Duane parameters using least squares.
| Run Number | Failed Unit | Test Time 1 | Test Time 2 | Cumulative Time |
|---|---|---|---|---|
| 1 | 1 | 0.2 | 2.0 | 2.2 |
| 2 | 2 | 1.7 | 2.9 | 4.6 |
| 3 | 2 | 4.5 | 5.2 | 9.7 |
| 4 | 2 | 5.8 | 9.1 | 14.9 |
| 5 | 2 | 17.3 | 9.2 | 26.5 |
| 6 | 2 | 29.3 | 24.1 | 53.4 |
| 7 | 1 | 36.5 | 61.1 | 97.6 |
| 8 | 2 | 46.3 | 69.6 | 115.9 |
| 9 | 1 | 63.6 | 78.1 | 141.7 |
| 10 | 2 | 64.4 | 85.4 | 149.8 |
| 11 | 1 | 74.3 | 93.6 | 167.9 |
| 12 | 1 | 106.6 | 103 | 209.6 |
| 13 | 2 | 195.2 | 117 | 312.2 |
| 14 | 2 | 235.1 | 134.3 | 369.4 |
| 15 | 1 | 248.7 | 150.2 | 398.9 |
| 16 | 2 | 256.8 | 164.6 | 421.4 |
| 17 | 2 | 261.1 | 174.3 | 435.4 |
| 18 | 2 | 299.4 | 193.2 | 492.6 |
| 19 | 1 | 305.3 | 234.2 | 539.5 |
| 20 | 1 | 326.9 | 257.3 | 584.2 |
| 21 | 1 | 339.2 | 290.2 | 629.4 |
| 22 | 1 | 366.1 | 293.1 | 659.2 |
| 23 | 2 | 466.4 | 316.4 | 782.8 |
| 24 | 1 | 504 | 373.2 | 877.2 |
| 25 | 1 | 510 | 375.1 | 885.1 |
| 26 | 2 | 543.2 | 386.1 | 929.3 |
| 27 | 2 | 635.4 | 453.3 | 1088.7 |
| 28 | 1 | 641.2 | 485.8 | 1127 |
| 29 | 2 | 755.8 | 573.6 | 1329.4 |
Solution
The solution to this example follows the same procedure as the previous example. Therefore, from Table 4.4:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{29}{\mathop \sum }}\,\ln ({{T}_{i}})= & 154.151 \\ & \underset{i=1}{\overset{29}{\mathop \sum }}\,\ln {{({{T}_{i}})}^{2}}= & 902.592 \\ & \underset{i=1}{\overset{29}{\mathop \sum }}\,\ln ({{m}_{c}})= & 82.884 \\ & \underset{i=1}{\overset{29}{\mathop \sum }}\,\ln ({{T}_{i}})\cdot \ln ({{m}_{c}})= & 483.154 \end{align} }[/math]
For least squares, Eqn. (Dalpha) is used to estimate [math]\displaystyle{ \alpha \,\! }[/math] :
- [math]\displaystyle{ \begin{align} & \widehat{\alpha }= & \frac{483.154-\tfrac{154.151\cdot 82.884}{29}}{902.592-\tfrac{{{(154.151)}^{2}}}{29}} \\ & = & 0.5115 \end{align} }[/math]
The estimator of [math]\displaystyle{ b\,\! }[/math] can be estimated from Eqn. (Dbi):
- [math]\displaystyle{ \begin{align} & \widehat{b}= & {{e}^{\tfrac{1}{29}(82.884-0.5115\cdot 154.151)}} \\ & = & 1.1495 \end{align} }[/math]
Therefore, from Eqn. (duane6):
- [math]\displaystyle{ {{\hat{m}}_{c}}=1.1495\cdot {{T}^{0.5115}} }[/math]
Using Eqn. (eq76), the equation for the instantaneous MTBF growth curve is:
- [math]\displaystyle{ {{\hat{m}}_{i}}=\frac{1}{1-0.5115}(1.1495){{T}^{0.5115}} }[/math]
Maximum Likelihood Estimators
In "Reliability Analysis for Complex, Repairable Systems"" (1974), L. H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. The Crow-AMSAA model, which is described in the next chapter, provides a complete Maximum Likelihood Estimation (MLE) solution to the Duane model.
Confidence Bounds
Least squares confidence bounds can be computed for both the model parameters and metrics of interest for the Duane model.
Parameter Bounds
Apply least squares analysis on the Duane model:
- [math]\displaystyle{ \ln ({{\hat{m}}_{c}})=\ln (b)+\alpha \ln (t) }[/math]
The unbiased estimator of [math]\displaystyle{ {{\sigma}^{2}}\,\! }[/math] can be obtained from:
- [math]\displaystyle{ {{\sigma }^{2}}=Var\left[ \ln {{m}_{c}}(t) \right]=\frac{SSE}{(n-2)} }[/math]
where:
- [math]\displaystyle{ SSE=\underset{i=1}{\overset{n}{\mathop \sum }}\,{{\left[ \ln {{{\hat{m}}}_{c}}({{t}_{i}})-\ln {{m}_{c}}({{t}_{i}}) \right]}^{2}} }[/math]
Thus, the confidence bounds on [math]\displaystyle{ \alpha \,\! }[/math] and [math]\displaystyle{ b\,\! }[/math] are:
- [math]\displaystyle{ C{{B}_{\alpha }}=\hat{\alpha }\pm {{t}_{n-2,\alpha /2}}SE(\hat{\alpha }) }[/math]
- [math]\displaystyle{ C{{B}_{b}}=\hat{b}{{e}^{\pm {{t}_{n-2,\alpha /2}}SE\left[ \ln (\hat{b}) \right]}} }[/math]
where [math]\displaystyle{ {{t}_{n-2,\alpha /2}}\,\! }[/math] denotes the percentage point of the [math]\displaystyle{ t\,\! }[/math] distribution with [math]\displaystyle{ n-2\,\! }[/math] degrees of freedom such that [math]\displaystyle{ P\{{{t}_{n-2}}\ge {{t}_{\alpha /2,n-2}}\}=\alpha /2\,\! }[/math] and:
- [math]\displaystyle{ SE(\hat{\alpha })=\frac{\sigma }{\sqrt{{{S}_{xx}}}} }[/math]
- [math]\displaystyle{ SE\left[ \ln (\hat{b}) \right]=\sigma \cdot \sqrt{\frac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{(\ln {{t}_{i}})}^{2}}}{n\cdot {{S}_{xx}}}} }[/math]
- [math]\displaystyle{ {{S}_{xx}}=\left[ \underset{i=1}{\overset{n}{\mathop \sum }}\,{{(\ln {{t}_{i}})}^{2}} \right]-\frac{1}{n}{{\left( \underset{i=1}{\overset{n}{\mathop \sum }}\,\ln ({{t}_{i}}) \right)}^{2}} }[/math]
Other Bounds
Confidence bounds also can be obtained on the cumulative MTBF and the cumulative failure intensity:
- [math]\displaystyle{ C{{B}_{{{m}_{c}}}}={{\hat{m}}_{c}}(t){{e}^{\pm {{z}_{\alpha }}\sqrt{Var\left[ \ln ({{{\hat{m}}}_{c}}) \right]}}} }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{\lambda }_{c}}(t)]}_{L}}= & \frac{1}{{{[{{m}_{c}}(t)]}_{u}}} \\ & {{[{{\lambda }_{c}}(t)]}_{U}}= & \frac{1}{{{[{{m}_{c}}(t)]}_{l}}} \end{align} }[/math]
When [math]\displaystyle{ n\,\! }[/math] is large, the approximate [math]\displaystyle{ 100(1-\alpha )%\,\! }[/math] confidence bounds for instantaneous MTBF are given by:
- [math]\displaystyle{ \begin{align} & {{m}_{i}}{{(t)}_{L}}= & \frac{{{[{{m}_{c}}(t)]}_{L}}}{{\hat{\beta }}} \\ & {{m}_{i}}{{(t)}_{U}}= & \frac{{{[{{m}_{c}}(t)]}_{U}}}{{\hat{\beta }}} \end{align} }[/math]
and therefore, the confidence bounds on the instantaneous failure intensity are:
- [math]\displaystyle{ \begin{align} & {{[{{\lambda }_{i}}(t)]}_{L}}= & \frac{1}{{{[{{m}_{i}}(t)]}_{U}}} \\ & {{[{{\lambda }_{c}}(t)]}_{U}}= & \frac{1}{{{[{{m}_{i}}(t)]}_{L}}} \end{align} }[/math]
Duane Confidence Bounds Example
For the data given above in Least Squares Example 2, calculate the 90% confidence bounds for:
- The parameters [math]\displaystyle{ \alpha\,\! }[/math] and [math]\displaystyle{ b\,\! }[/math].
- The cumulative and instantaneous failure intensity.
- The cumulative and instantaneous MTBF.
Solution
- 1. Using the values of [math]\displaystyle{ \widehat{b}\,\! }[/math] and [math]\displaystyle{ \widehat{\alpha }\,\! }[/math] estimated from the least squares analysis in Example 3:
- [math]\displaystyle{ \widehat{b}=1.9453 }[/math]
- [math]\displaystyle{ \widehat{\alpha}=0.6133 Eqn. (duanec9) is: ::\lt math\gt \begin{align} & {{S}_{xx}}= & 1400.9084-1301.4545 \\ & = & 99.4539 \end{align} }[/math]
Eqn. (duanec7) is:
- [math]\displaystyle{ \begin{align} & SE(\hat{\alpha })= & \frac{\sigma }{\sqrt{{{S}_{xx}}}} \\ & = & \frac{0.08428}{9.9727} \\ & = & 0.008452 \end{align} }[/math]
Eqn. (duanec8) is:
- [math]\displaystyle{ \begin{align} & SE(\ln \hat{b})= & \sigma \cdot \sqrt{\frac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{(\ln {{T}_{i}})}^{2}}}{n\cdot {{S}_{xx}}}} \\ & = & 0.065960 \end{align} }[/math]
Thus, 90% confidence bounds on parameter [math]\displaystyle{ \alpha \,\! }[/math] using Eqn. (duanec1) are:
- [math]\displaystyle{ \begin{align} & {{\alpha }_{L}}= & 0.602050 \\ & {{\alpha }_{U}}= & 0.624417 \end{align} }[/math]
And 90% confidence bounds on parameter [math]\displaystyle{ b\,\! }[/math] using Eqn. (duanec2) are:
- [math]\displaystyle{ \begin{align} & {{b}_{L}}= & 1.7831 \\ & {{b}_{U}}= & 2.1231 \end{align} }[/math]
- 2. The cumulative failure intensity is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{c}}= & \frac{1}{1.9453}\cdot {{22000}^{-0.6133}} \\ & = & 0.00111689 \end{align} }[/math]
And the instantaneous failure intensity is equal to:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{i}}= & \frac{1}{1.9453}\cdot (1-0.6133)\cdot {{22000}^{-0.6133}} \\ & = & 0.00043198 \end{align} }[/math]
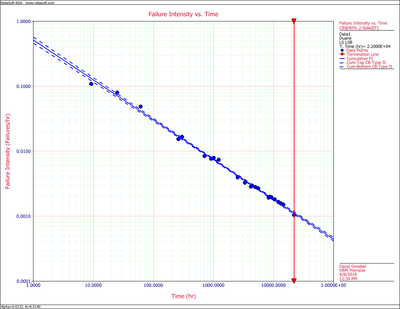
So, at the 90% confidence level and for [math]\displaystyle{ T=22,000\,\! }[/math] hr, the confidence bounds on cumulative failure intensity are:
- [math]\displaystyle{ \begin{align} & {{[{{\lambda }_{c}}(t)]}_{L}}= & 0.00100254 \\ & {{[{{\lambda }_{c}}(t)]}_{U}}= & 0.00124429 \end{align} }[/math]
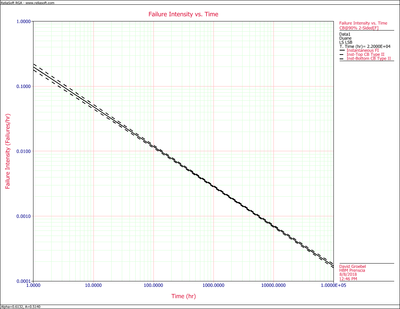
For the instantaneous failure intensity:
- [math]\displaystyle{ \begin{align} & {{[{{\lambda }_{i}}(t)]}_{L}}= & 0.00038775 \\ & {{[{{\lambda }_{c}}(t)]}_{U}}= & 0.00048125 \end{align} }[/math]
Figures figure75 and figure76 show the graphs of the cumulative and instantaneous failure intensity. Both are plotted with confidence bounds.
- 3. The cumulative MTBF is:
- [math]\displaystyle{ \begin{align} & {{m}_{c}}(T)= & 1.9453\cdot {{22000}^{0.6133}} \\ & = & 895.3395 \end{align} }[/math]
And the instantaneous MTBF is:
- [math]\displaystyle{ \begin{align} & {{m}_{i}}(T)= & \frac{1.9453}{1-0.6133}\cdot {{22000}^{0.6133}} \\ & = & 2314.9369 \end{align} }[/math]
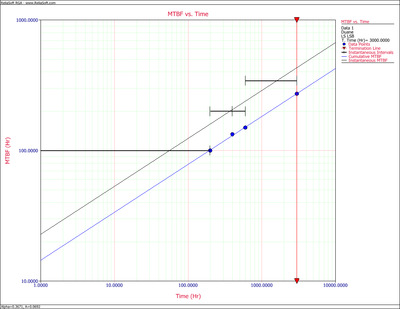
So, at 90% confidence level and for [math]\displaystyle{ T=22,000\,\! }[/math] hr, the confidence bounds on the cumulative MTBF are:
- [math]\displaystyle{ \begin{align} & {{m}_{c}}{{(t)}_{l}}= & 803.6695 \\ & {{m}_{c}}{{(t)}_{u}}= & 997.4658 \end{align} }[/math]
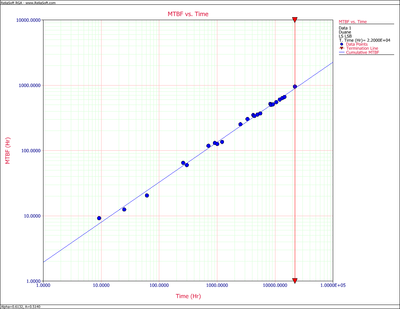
The confidence bounds for the instantaneous MTBF are:
- [math]\displaystyle{ \begin{align} & {{m}_{i}}{{(t)}_{l}}= & 2077.9204 \\ & {{m}_{i}}{{(t)}_{u}}= & 2578.9886 \end{align} }[/math]
Figure CumMTBFCB displays the cumulative MTBF while Figure InstMTBFCB displays the instantaneous MTBF. Both are plotted with confidence bounds.
More Examples
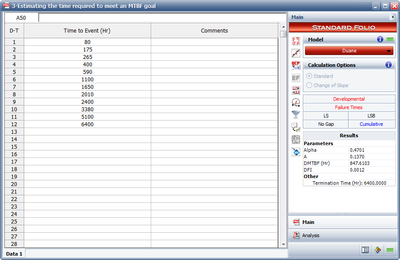
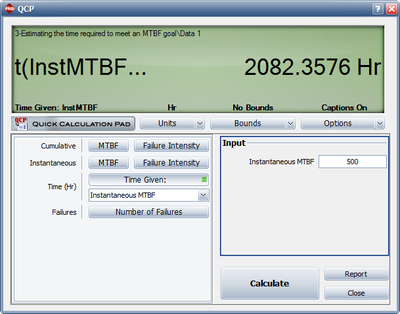
Estimating the Time Required to Meet an MTBF Goal
A prototype of a system was tested with design changes incorporated during the test. A total of 12 failures occurred. The data set is given in Table 4.5.
- Estimate the Duane parameters.
- Plot the cumulative and instantaneous MTBF curves.
- How many cumulative test and development hours are required to meet an instantaneous MTBF goal #of 500 hours?
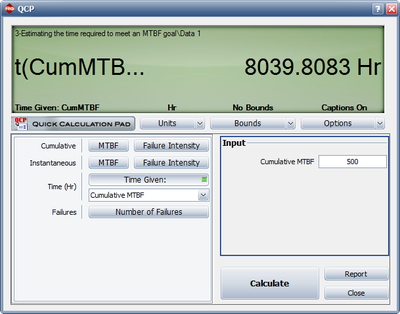
- How many cumulative test and development hours are required to meet a cumulative MTBF goal of 500 hours?
| Failure Number | Cumulative Test Time(hr) |
|---|---|
| 1 | 80 |
| 2 | 175 |
| 3 | 265 |
| 4 | 400 |
| 5 | 590 |
| 6 | 1100 |
| 7 | 1650 |
| 8 | 2010 |
| 9 | 2400 |
| 10 | 3380 |
| 11 | 5100 |
| 12 | 6400 |
Solution
- Figure figuaneex11 shows the data entered into RGA along with the estimated Duane parameters.
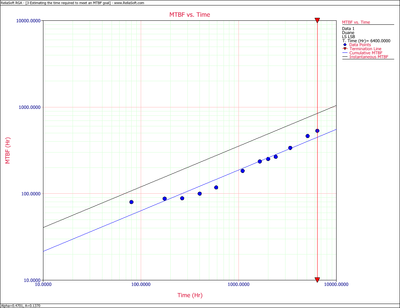
- Figure figuaneex12 shows the cumulative and instantaneous MTBF curves.
- Figure figuaneex14 shows the cumulative test and development hours needed for an instantaneous MTBF goal of 500 hours.
- Figure figuaneex15 shows the cumulative test and development hours needed for a cumulative MTBF goal of 500 hours.
Deciding Whether to Halt the Test
<<PER LISA: NEED TO GET SME TO CONFIRM THE NEW NAME FOR THIS EXAMPLE>>
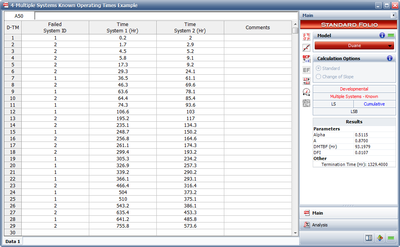
Two identical systems were tested. Any design changes made to improve the reliability of these systems were incorporated into both systems when any system failed. A total of 29 failures occurred. The data set is given in Table 4.6. Do the following:
- Estimate the Duane parameters.
- Assume both units are tested for an additional 100 hrs each. How many failures do you expect in that period?
- If testing/development were halted at this point, what would the reliability equation for this system be
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2 (hr) |
|---|---|---|---|
| 1 | 1 | 0.2 | 2.0 |
| 2 | 2 | 1.7 | 2.9 |
| 3 | 2 | 4.5 | 5.2 |
| 4 | 2 | 5.8 | 9.1 |
| 5 | 2 | 17.3 | 9.2 |
| 6 | 2 | 29.3 | 24.1 |
| 7 | 1 | 36.5 | 61.1 |
| 8 | 2 | 46.3 | 69.6 |
| 9 | 1 | 63.6 | 78.1 |
| 10 | 2 | 64.4 | 85.4 |
| 11 | 1 | 74.3 | 93.6 |
| 12 | 1 | 106.6 | 103 |
| 13 | 2 | 195.2 | 117 |
| 14 | 2 | 235.1 | 134.3 |
| 15 | 1 | 248.7 | 150.2 |
| 16 | 2 | 256.8 | 164.6 |
| 17 | 2 | 261.1 | 174.3 |
| 18 | 2 | 299.4 | 193.2 |
| 19 | 1 | 305.3 | 234.2 |
| 20 | 1 | 326.9 | 257.3 |
| 21 | 1 | 339.2 | 290.2 |
| 22 | 1 | 366.1 | 293.1 |
| 23 | 2 | 466.4 | 316.4 |
| 24 | 1 | 504 | 373.2 |
| 25 | 1 | 510 | 375.1 |
| 26 | 2 | 543.2 | 386.1 |
| 27 | 2 | 635.4 | 453.3 |
| 28 | 1 | 641.2 | 485.8 |
| 29 | 2 | 755.8 | 573.6 |
Solution
- 1) Figure figuaneex21 shows the data entered into RGA along with the estimated Duane parameters.
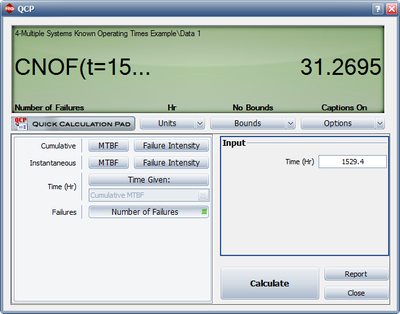
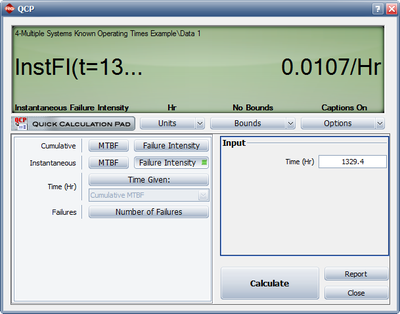
- 2) The current accumulated test time for both units is 1329.4 hr. If the process were to continue for an additional combined time of 200 hr, the expected cumulative number of failures at [math]\displaystyle{ T=1529.4 }[/math] is 31.2695, as shown in Figure figuaneex22. At T = 1329.4, the expected number of failures is 29.2004. Therefore, the expected number of failures that would be observed over the additional 200 hr is [math]\displaystyle{ 31.2695-29.2004=2.0691\approx 2 }[/math] .
- 3) If testing/development were halted at this point, the system failure intensity would be equal to the instantaneous failure intensity at that time, or [math]\displaystyle{ \lambda =0.0107 }[/math] failures/hr. See Figure figuaneex23. An exponential distribution can be assumed since the value of the failure intensity at that instant in time is known. Therefore:
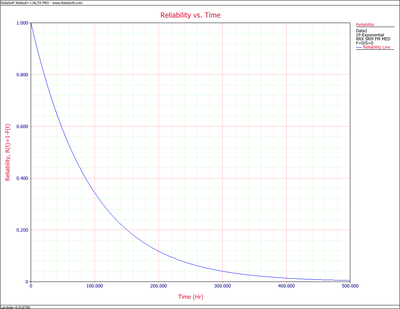
- [math]\displaystyle{ \begin{align} & R(t)= & {{e}^{-\lambda t}} \\ & = & {{e}^{-(0.0107)t}} \end{align} }[/math]
Weibull++ can be utilized (from within RGA) to provide a Reliability vs. Time plot. This is shown in Figure figuaneex24.
Using the Duane Model for Success/Failure Data
Given the sequential success/failure data in the Table 4.7, do the following:
- 1) Estimate the Duane parameters.
- 2) What is the instantaneous MTBF at the end of the test?
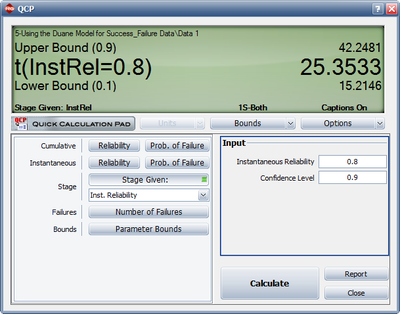
- 3) How many additional test runs with a one-sided 90% confidence level are required to meet an instantaneous MTBF goal of 5 hours?
| Run Number | Result |
|---|---|
| 1 | F |
| 2 | F |
| 3 | S |
| 4 | S |
| 5 | S |
| 6 | F |
| 7 | S |
| 8 | F |
| 9 | F |
| 10 | S |
| 11 | S |
| 12 | S |
| 13 | F |
| 14 | S |
| 15 | S |
| 16 | S |
| 17 | S |
| 18 | S |
| 19 | S |
| 20 | S |
Solution
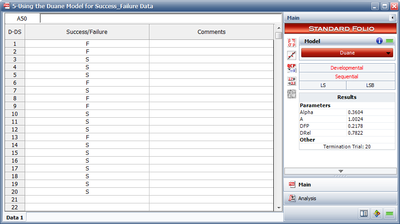
- 1) Figure figuaneex31 shows the data set entered into RGA along with the estimated Duane parameters.
- 2) The MTBF at the end of the test is equal to 4.5904 hours. Note that this is the DMTBF that is shown in the Control Panel in Figure figuaneex31.
- 3) Figure figuaneex34 shows the number of test runs with both one-sided confidence bounds at 90% confidence level to achieve an instantaneous MTBF of 5 hours. Therefore, the number of additional test runs required with a 90% confidence level is equal to [math]\displaystyle{ 42.2481-20=22.2481\approx 23 }[/math] test runs.