Crow-AMSAA Confidence Bounds

In this appendix, we will present the two methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA (NHPP) model when applied to developmental testing data. The Fisher Matrix approach is based on the Fisher Information Matrix and is commonly employed in the reliability field. The Crow bounds were developed by Dr. Larry Crow.

Individual (Non-Grouped) Data

Bounds on Beta

Fisher Matrix Bounds

The parameter [math]\displaystyle{ \beta }[/math] must be positive, thus [math]\displaystyle{ \ln \beta }[/math] is treated as being normally distributed as well.

[math]\displaystyle{ \frac{\ln \hat{\beta }-\ln \beta }{\sqrt{Var(\ln \hat{\beta }})}\ \tilde{\ }\ N(0,1) }[/math]

The approximate confidence bounds are given as:

[math]\displaystyle{ C{{B}_{\beta }}=\hat{\beta }{{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} }[/math]

[math]\displaystyle{ \alpha }[/math] in [math]\displaystyle{ {{z}_{\alpha }} }[/math] is different ( [math]\displaystyle{ \alpha /2 }[/math] , [math]\displaystyle{ \alpha }[/math] ) according to a 2-sided confidence interval or a 1-sided confidence interval, and variances can be calculated using the Fisher Matrix.

[math]\displaystyle{ \left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\lambda }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \lambda \partial \beta } \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial \lambda \partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\beta }^{2}}} \\ \end{matrix} \right]_{\beta =\widehat{\beta },\lambda =\widehat{\lambda }}^{-1}=\left[ \begin{matrix} Var(\widehat{\lambda }) & Cov(\widehat{\beta },\widehat{\lambda }) \\ Cov(\widehat{\beta },\widehat{\lambda }) & Var(\widehat{\beta }) \\ \end{matrix} \right] }[/math]

[math]\displaystyle{ \Lambda }[/math] is the natural log-likelihood function:

[math]\displaystyle{ \Lambda =N\ln \lambda +N\ln \beta -\lambda {{T}^{\beta }}+(\beta -1)\underset{i=1}{\overset{N}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]

[math]\displaystyle{ \frac{{{\partial }^{2}}\Lambda }{\partial {{\lambda }^{2}}}=-\frac{N}{{{\lambda }^{2}}} }[/math]

and:

[math]\displaystyle{ \frac{{{\partial }^{2}}\Lambda }{\partial {{\beta }^{2}}}=-\frac{N}{{{\beta }^{2}}}-\lambda {{T}^{\beta }}{{(\ln T)}^{2}} }[/math]

also:

[math]\displaystyle{ \frac{{{\partial }^{2}}\Lambda }{\partial \lambda \partial \beta }=-{{T}^{\beta }}\ln T }[/math]

Crow Bounds

Time Terminated Data

For the 2-sided [math]\displaystyle{ (1-\alpha ) }[/math] 100-percent confidence interval on [math]\displaystyle{ \beta }[/math] , calculate:

[math]\displaystyle{ \begin{align} & {{D}_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2(N-1)} \\ & {{D}_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N}^{2}}{2(N-1)} \end{align} }[/math]

The fractiles can be found in the tables of the [math]\displaystyle{ {{\chi }^{2}} }[/math] distribution. Thus the confidence bounds on [math]\displaystyle{ \beta }[/math] are:

[math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & {{D}_{L}}\cdot \hat{\beta } \\ & {{\beta }_{U}}= & {{D}_{U}}\cdot \hat{\beta } \end{align} }[/math]

Failure Terminated Data
For the 2-sided [math]\displaystyle{ (1-\alpha ) }[/math] 100-percent confidence interval on [math]\displaystyle{ \beta }[/math] , calculate:

[math]\displaystyle{ \begin{align} & {{D}_{L}}= & \frac{N\cdot \chi _{\tfrac{\alpha }{2},2(N-1)}^{2}}{2(N-1)(N-2)} \\ & {{D}_{U}}= & \frac{N\cdot \chi _{1-\tfrac{\alpha }{2},2(N-1)}^{2}}{2(N-1)(N-2)} \end{align} }[/math]

Thus the confidence bounds on [math]\displaystyle{ \beta }[/math] are:

[math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & {{D}_{L}}\cdot \hat{\beta } \\ & {{\beta }_{U}}= & {{D}_{U}}\cdot \hat{\beta } \end{align} }[/math]

Bounds on Lambda

Fisher Matrix Bounds

The parameter [math]\displaystyle{ \lambda }[/math] must be positive, thus [math]\displaystyle{ \ln \lambda }[/math] is treated as being normally distributed as well. These bounds are based on:

[math]\displaystyle{ \frac{\ln \hat{\lambda }-\ln \lambda }{\sqrt{Var(\ln \hat{\lambda }})}\ \tilde{\ }\ N(0,1) }[/math]

The approximate confidence bounds on [math]\displaystyle{ \lambda }[/math] are given as:

[math]\displaystyle{ C{{B}_{\lambda }}=\hat{\lambda }{{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} }[/math]

where:

[math]\displaystyle{ \hat{\lambda }=\frac{n}{{{T}^{*\hat{\beta }}}} }[/math]

The variance calculation is the same as Eqn. (variance1).

Crow Bounds

Time Terminated Data
For the 2-sided [math]\displaystyle{ (1-\alpha ) }[/math] 100-percent confidence interval, the confidence bounds on [math]\displaystyle{ \lambda }[/math] are:

[math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2{{T}^{{\hat{\beta }}}}} \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2{{T}^{{\hat{\beta }}}}} \end{align} }[/math]

The fractiles can be found in the tables of the [math]\displaystyle{ {{\chi }^{2}} }[/math] distribution.

Failure Terminated Data
For the 2-sided [math]\displaystyle{ (1-\alpha ) }[/math] 100-percent confidence interval, the confidence bounds on [math]\displaystyle{ \lambda }[/math] are:

[math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2{{T}^{{\hat{\beta }}}}} \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N}^{2}}{2{{T}^{{\hat{\beta }}}}} \end{align} }[/math]

Bounds on Growth Rate

Since the growth rate is equal to [math]\displaystyle{ 1-\beta }[/math] , the confidence bounds for both the Fisher Matrix and Crow methods are:

[math]\displaystyle{ G\text{row}th Rate_L=1-\beta_U }[/math]

[math]\displaystyle{ G\text{row}th Rate_U=1-\beta_L }[/math]

For the Fisher Matrix confidence bounds, [math]\displaystyle{ {{\beta }_{L}} }[/math] and [math]\displaystyle{ {{\beta }_{U}} }[/math] are obtained from Eqn. (amsaac1). For the Crow bounds, [math]\displaystyle{ {{\beta }_{L}} }[/math] and [math]\displaystyle{ {{\beta }_{U}} }[/math] are obtained from Eqns. (amsaac2) and (amsaac22) depending on whether the analysis is for time terminated data or failure terminated data.

Bounds on Cumulative MTBF

Fisher Matrix Bounds

The cumulative MTBF, [math]\displaystyle{ {{m}_{c}}(t) }[/math] , must be positive, thus [math]\displaystyle{ \ln {{m}_{c}}(t) }[/math] is treated as being normally distributed as well.

[math]\displaystyle{ \frac{\ln {{{\hat{m}}}_{c}}(t)-\ln {{m}_{c}}(t)}{\sqrt{Var(\ln {{{\hat{m}}}_{c}}(t)})}\ \tilde{\ }\ N(0,1) }[/math]

The approximate confidence bounds on the cumulative MTBF are then estimated from:

[math]\displaystyle{ CB={{\hat{m}}_{c}}(t){{e}^{\pm {{z}_{\alpha }}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} }[/math]

where:

[math]\displaystyle{ {{\hat{m}}_{c}}(t)=\frac{1}{{\hat{\lambda }}}{{t}^{1-\hat{\beta }}} }[/math]

[math]\displaystyle{ \begin{align} & Var({{{\hat{m}}}_{c}}(t))= & {{\left( \frac{\partial {{m}_{c}}(t)}{\partial \beta } \right)}^{2}}Var(\hat{\beta })+{{\left( \frac{\partial {{m}_{c}}(t)}{\partial \lambda } \right)}^{2}}Var(\hat{\lambda }) \\ & & +2\left( \frac{\partial {{m}_{c}}(t)}{\partial \beta } \right)\left( \frac{\partial {{m}_{c}}(t)}{\partial \lambda } \right)cov(\hat{\beta },\hat{\lambda })\, \end{align} }[/math]

The variance calculation is the same as Eqn. (variance1) and:

[math]\displaystyle{ \begin{align} & \frac{\partial {{m}_{c}}(t)}{\partial \beta }= & -\frac{1}{{\hat{\lambda }}}{{t}^{1-\hat{\beta }}}\ln t \\ & \frac{\partial {{m}_{c}}(t)}{\partial \lambda }= & -\frac{1}{{{{\hat{\lambda }}}^{2}}}{{t}^{1-\hat{\beta }}} \end{align} }[/math]

Crow Bounds

To calculate the Crow confidence bounds on cumulative MTBF, first calculate the Crow cumulative failure intensity confidence bounds:

[math]\displaystyle{ C{{(t)}_{L}}=\frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot t} }[/math]

[math]\displaystyle{ C{{(t)}_{U}}=\frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot t} }[/math]

Then:

[math]\displaystyle{ \begin{align} & {{[MTB{{F}_{c}}]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & {{[MTB{{F}_{c}}]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \end{align} }[/math]

Bounds on Instantaneous MTBF

Fisher Matrix Bounds

The instantaneous MTBF, [math]\displaystyle{ {{m}_{i}}(t) }[/math] , must be positive, thus [math]\displaystyle{ \ln {{m}_{i}}(t) }[/math] is treated as being normally distributed as well.

[math]\displaystyle{ \frac{\ln {{{\hat{m}}}_{i}}(t)-\ln {{m}_{i}}(t)}{\sqrt{Var(\ln {{{\hat{m}}}_{i}}(t)})}\ \tilde{\ }\ N(0,1) }[/math]

The approximate confidence bounds on the instantaneous MTBF are then estimated from:

[math]\displaystyle{ CB={{\hat{m}}_{i}}(t){{e}^{\pm {{z}_{\alpha }}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} }[/math]

where:

[math]\displaystyle{ {{\hat{m}}_{i}}(t)=\frac{1}{\lambda \beta {{t}^{\beta -1}}} }[/math]

[math]\displaystyle{ \begin{align} & Var({{{\hat{m}}}_{i}}(t))= & {{\left( \frac{\partial {{m}_{i}}(t)}{\partial \beta } \right)}^{2}}Var(\hat{\beta })+{{\left( \frac{\partial {{m}_{i}}(t)}{\partial \lambda } \right)}^{2}}Var(\hat{\lambda }) \\ & & +2\left( \frac{\partial {{m}_{i}}(t)}{\partial \beta } \right)\left( \frac{\partial {{m}_{i}}(t)}{\partial \lambda } \right)cov(\hat{\beta },\hat{\lambda }). \end{align} }[/math]

The variance calculation is the same as Eqn. (variance1) and:

[math]\displaystyle{ \begin{align} & \frac{\partial {{m}_{i}}(t)}{\partial \beta }= & -\frac{1}{\hat{\lambda }{{{\hat{\beta }}}^{2}}}{{t}^{1-\hat{\beta }}}-\frac{1}{\hat{\lambda }\hat{\beta }}{{t}^{1-\hat{\beta }}}\ln t \\ & \frac{\partial {{m}_{i}}(t)}{\partial \lambda }= & -\frac{1}{{{{\hat{\lambda }}}^{2}}\hat{\beta }}{{t}^{1-\hat{\beta }}} \end{align} }[/math]

Crow Bounds

Failure Terminated Data
Consider the following equation:

[math]\displaystyle{ G(\mu |n)=\mathop{}_{0}^{\infty }\frac{{{e}^{-x}}{{x}^{n-2}}}{(n-2)!}\underset{i=0}{\overset{n-1}{\mathop \sum }}\,\frac{1}{i!}{{\left( \frac{\mu }{x} \right)}^{i}}\exp (-\frac{\mu }{x})\,dx }[/math]

Find the values [math]\displaystyle{ {{p}_{1}} }[/math] and [math]\displaystyle{ {{p}_{2}} }[/math] by finding the solution [math]\displaystyle{ c }[/math] to [math]\displaystyle{ G({{n}^{2}}/c|n)=\xi }[/math] for [math]\displaystyle{ \xi =\tfrac{\alpha }{2} }[/math] and [math]\displaystyle{ \xi =1-\tfrac{\alpha }{2} }[/math] , respectively. If using the biased parameters, [math]\displaystyle{ \hat{\beta } }[/math] and [math]\displaystyle{ \hat{\lambda } }[/math] , then the upper and lower confidence bounds are:

[math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & MTB{{F}_{i}}\cdot {{p}_{1}} \\ & {{[MTB{{F}_{i}}]}_{U}}= & MTB{{F}_{i}}\cdot {{p}_{2}} \end{align} }[/math]

where [math]\displaystyle{ MTB{{F}_{i}}=\tfrac{1}{\hat{\lambda }\hat{\beta }{{t}^{\hat{\beta }-1}}} }[/math] . If using the unbiased parameters, [math]\displaystyle{ \bar{\beta } }[/math] and [math]\displaystyle{ \bar{\lambda } }[/math] , then the upper and lower confidence bounds are:

[math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & MTB{{F}_{i}}\cdot \left( \frac{N-2}{N} \right)\cdot {{p}_{1}} \\ & {{[MTB{{F}_{i}}]}_{U}}= & MTB{{F}_{i}}\cdot \left( \frac{N-2}{N} \right)\cdot {{p}_{2}} \end{align} }[/math]

where [math]\displaystyle{ MTB{{F}_{i}}=\tfrac{1}{\hat{\lambda }\hat{\beta }{{t}^{\hat{\beta }-1}}} }[/math] .

Time Terminated Data
Consider the following equation where [math]\displaystyle{ {{I}_{1}}(.) }[/math] is the modified Bessel function of order one:

[math]\displaystyle{ H(x|k)=\underset{j=1}{\overset{k}{\mathop \sum }}\,\frac{{{x}^{2j-1}}}{{{2}^{2j-1}}(j-1)!j!{{I}_{1}}(x)} }[/math]

Find the values [math]\displaystyle{ {{\Pi }_{1}} }[/math] and [math]\displaystyle{ {{\Pi }_{2}} }[/math] by finding the solution [math]\displaystyle{ x }[/math] to [math]\displaystyle{ H(x|k)=\tfrac{\alpha }{2} }[/math] and [math]\displaystyle{ H(x|k)=1-\tfrac{\alpha }{2} }[/math] in the cases corresponding to the lower and upper bounds, respectively. Calculate [math]\displaystyle{ \Pi =\tfrac{4{{n}^{2}}}{{{x}^{2}}} }[/math] for each case. If using the biased parameters, [math]\displaystyle{ \hat{\beta } }[/math] and [math]\displaystyle{ \hat{\lambda } }[/math] , then the upper and lower confidence bounds are:

[math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & MTB{{F}_{i}}\cdot {{\Pi }_{1}} \\ & {{[MTB{{F}_{i}}]}_{U}}= & MTB{{F}_{i}}\cdot {{\Pi }_{2}} \end{align} }[/math]

where [math]\displaystyle{ MTB{{F}_{i}}=\tfrac{1}{\hat{\lambda }\hat{\beta }{{t}^{\hat{\beta }-1}}} }[/math] . If using the unbiased parameters, [math]\displaystyle{ \bar{\beta } }[/math] and [math]\displaystyle{ \bar{\lambda } }[/math] , then the upper and lower confidence bounds are:

[math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & MTB{{F}_{i}}\cdot \left( \frac{N-1}{N} \right)\cdot {{\Pi }_{1}} \\ & {{[MTB{{F}_{i}}]}_{U}}= & MTB{{F}_{i}}\cdot \left( \frac{N-1}{N} \right)\cdot {{\Pi }_{2}} \end{align} }[/math]

where [math]\displaystyle{ MTB{{F}_{i}}=\tfrac{1}{\hat{\lambda }\hat{\beta }{{t}^{\hat{\beta }-1}}} }[/math] .

Bounds on Cumulative Failure Intensity

Fisher Matrix Bounds

The cumulative failure intensity, [math]\displaystyle{ {{\lambda }_{c}}(t) }[/math] , must be positive, thus [math]\displaystyle{ \ln {{\lambda }_{c}}(t) }[/math] is treated as being normally distributed.

[math]\displaystyle{ \frac{\ln {{{\hat{\lambda }}}_{c}}(t)-\ln {{\lambda }_{c}}(t)}{\sqrt{Var(\ln {{{\hat{\lambda }}}_{c}}(t)})}\ \tilde{\ }\ N(0,1) }[/math]

The approximate confidence bounds on the cumulative failure intensity are then estimated from:

[math]\displaystyle{ CB={{\hat{\lambda }}_{c}}(t){{e}^{\pm {{z}_{\alpha }}\sqrt{Var({{{\hat{\lambda }}}_{c}}(t))}/{{{\hat{\lambda }}}_{c}}(t)}} }[/math]

where:

[math]\displaystyle{ {{\hat{\lambda }}_{c}}(t)=\hat{\lambda }{{t}^{\hat{\beta }-1}} }[/math]

and:

[math]\displaystyle{ \begin{align} & Var({{{\hat{\lambda }}}_{c}}(t))= & {{\left( \frac{\partial {{\lambda }_{c}}(t)}{\partial \beta } \right)}^{2}}Var(\hat{\beta })+{{\left( \frac{\partial {{\lambda }_{c}}(t)}{\partial \lambda } \right)}^{2}}Var(\hat{\lambda }) \\ & & +2\left( \frac{\partial {{\lambda }_{c}}(t)}{\partial \beta } \right)\left( \frac{\partial {{\lambda }_{c}}(t)}{\partial \lambda } \right)cov(\hat{\beta },\,\,\,\hat{\lambda }) \end{align} }[/math]

The variance calculation is the same as Eqn. (variance1) and:

[math]\displaystyle{ \begin{align} & \frac{\partial {{\lambda }_{c}}(t)}{\partial \beta }= & \hat{\lambda }{{t}^{\hat{\beta }-1}}\ln t \\ & \frac{\partial {{\lambda }_{c}}(t)}{\partial \lambda }= & {{t}^{\hat{\beta }-1}} \end{align} }[/math]

Crow Bounds

The Crow cumulative failure intensity confidence bounds are given as:

[math]\displaystyle{ \begin{align} & C{{(t)}_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot t} \\ & C{{(t)}_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot t} \end{align} }[/math]

Bounds on Instantaneous Failure Intensity

Fisher Matrix Bounds

The instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(t) }[/math] , must be positive, thus [math]\displaystyle{ \ln {{\lambda }_{i}}(t) }[/math] is treated as being normally distributed.

[math]\displaystyle{ \frac{\ln {{{\hat{\lambda }}}_{i}}(t)-\ln {{\lambda }_{i}}(t)}{\sqrt{Var(\ln {{{\hat{\lambda }}}_{i}}(t)})}\text{ }\tilde{\ }\text{ }N(0,1) }[/math]

The approximate confidence bounds on the instantaneous failure intensity are then estimated from:

[math]\displaystyle{ CB={{\hat{\lambda }}_{i}}(t){{e}^{\pm {{z}_{\alpha }}\sqrt{Var({{{\hat{\lambda }}}_{i}}(t))}/{{{\hat{\lambda }}}_{i}}(t)}} }[/math]

where

[math]\displaystyle{ {{\lambda }_{i}}(t)=\lambda \beta {{t}^{\beta -1}} }[/math]

[math]\displaystyle{ \begin{align} & Var({{{\hat{\lambda }}}_{i}}(t))= & {{\left( \frac{\partial {{\lambda }_{i}}(t)}{\partial \beta } \right)}^{2}}Var(\hat{\beta })+{{\left( \frac{\partial {{\lambda }_{i}}(t)}{\partial \lambda } \right)}^{2}}Var(\hat{\lambda }) \\ & & +2\left( \frac{\partial {{\lambda }_{i}}(t)}{\partial \beta } \right)\left( \frac{\partial {{\lambda }_{i}}(t)}{\partial \lambda } \right)cov(\hat{\beta },\,\,\,\hat{\lambda }) \end{align} }[/math]

The variance calculation is the same as Eqn. (variance1) and:

[math]\displaystyle{ \begin{align} & \frac{\partial {{\lambda }_{i}}(t)}{\partial \beta }= & \hat{\lambda }{{t}^{\hat{\beta }-1}}+\hat{\lambda }\hat{\beta }{{t}^{\hat{\beta }-1}}\ln t \\ & \frac{\partial {{\lambda }_{i}}(t)}{\partial \lambda }= & \hat{\beta }{{t}^{\hat{\beta }-1}} \end{align} }[/math]

Crow Bounds

The Crow instantaneous failure intensity confidence bounds are given as:

[math]\displaystyle{ \begin{align} & {{\lambda }_{i}}{{(t)}_{L}}= & \frac{1}{{{[MTB{{F}_{i}}]}_{U}}} \\ & {{\lambda }_{i}}{{(t)}_{U}}= & \frac{1}{{{[MTB{{F}_{i}}]}_{L}}} \end{align} }[/math]

Bounds on Time Given Cumulative Failure Intensity

Fisher Matrix Bounds

The time, [math]\displaystyle{ T }[/math] , must be positive, thus [math]\displaystyle{ \ln T }[/math] is treated as being normally distributed.

[math]\displaystyle{ \frac{\ln \hat{T}-\ln T}{\sqrt{Var(\ln \hat{T}})}\ \tilde{\ }\ N(0,1) }[/math]

Confidence bounds on the time are given by:

[math]\displaystyle{ CB=\hat{T}{{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\hat{T})}/\hat{T}}} }[/math]

where:

[math]\displaystyle{ \begin{align} & Var(\hat{T})= & {{\left( \frac{\partial T}{\partial \beta } \right)}^{2}}Var(\hat{\beta })+{{\left( \frac{\partial T}{\partial \lambda } \right)}^{2}}Var(\hat{\lambda }) \\ & & +2\left( \frac{\partial T}{\partial \beta } \right)\left( \frac{\partial T}{\partial \lambda } \right)cov(\hat{\beta },\,\,\,\hat{\lambda }) \end{align} }[/math]

The variance calculation is the same as Eqn. (variance1) and:

[math]\displaystyle{ \begin{align} & \frac{\partial T}{\partial \beta }= & \frac{-{{\left( \tfrac{{{\lambda }_{c}}(T)}{\lambda } \right)}^{1/(\beta -1)}}\ln \left( \tfrac{{{\lambda }_{c}}(T)}{\lambda } \right)}{{{(1-\beta )}^{2}}} \\ & \frac{\partial T}{\partial \lambda }= & {{\left( \frac{{{\lambda }_{c}}(T)}{\lambda } \right)}^{1/(\beta -1)}}\frac{1}{\lambda (1-\beta )} \end{align} }[/math]

Crow Bounds

Step 1: Calculate:

[math]\displaystyle{ \hat{T}={{\left( \frac{{{\lambda }_{c}}(T)}{{\hat{\lambda }}} \right)}^{\tfrac{1}{\beta -1}}} }[/math]

Step 2: Estimate the number of failures:

[math]\displaystyle{ N(\hat{T})=\hat{\lambda }{{\hat{T}}^{{\hat{\beta }}}} }[/math]

Step 3: Obtain the confidence bounds on time given the cumulative failure intensity by solving for [math]\displaystyle{ {{t}_{l}} }[/math] and [math]\displaystyle{ {{t}_{u}} }[/math] in the following equations:

[math]\displaystyle{ \begin{align} & {{t}_{l}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot {{\lambda }_{c}}(T)} \\ & {{t}_{u}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot {{\lambda }_{c}}(T)} \end{align} }[/math]

Bounds on Time Given Cumulative MTBF

Fisher Matrix Bounds

The time, [math]\displaystyle{ T }[/math] , must be positive, thus [math]\displaystyle{ \ln T }[/math] is treated as being normally distributed.

[math]\displaystyle{ \frac{\ln \hat{T}-\ln T}{\sqrt{Var(\ln \hat{T}})}\ \tilde{\ }\ N(0,1) }[/math]

Confidence bounds on the time are given by:

[math]\displaystyle{ CB=\hat{T}{{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\hat{T})}/\hat{T}}} }[/math]

where:

[math]\displaystyle{ \begin{align} & Var(\hat{T})= & {{\left( \frac{\partial T}{\partial \beta } \right)}^{2}}Var(\hat{\beta })+{{\left( \frac{\partial T}{\partial \lambda } \right)}^{2}}Var(\hat{\lambda }) \\ & & +2\left( \frac{\partial T}{\partial \beta } \right)\left( \frac{\partial T}{\partial \lambda } \right)cov(\hat{\beta },\,\,\,\hat{\lambda }) \end{align} }[/math]

The variance calculation is the same as Eqn. (variance1) and:

[math]\displaystyle{ \hat{T}={{(\lambda \cdot {{m}_{c}})}^{1/(1-\beta )}} }[/math]

[math]\displaystyle{ \begin{align} & \frac{\partial T}{\partial \beta }= & \frac{{{(\lambda \cdot \,{{m}_{c}})}^{1/(1-\beta )}}\ln (\lambda \cdot \text{ }{{m}_{c}})}{{{(1-\beta )}^{2}}} \\ & \frac{\partial T}{\partial \lambda }= & \frac{{{(\lambda \text{ }\cdot \text{ }{{m}_{c}})}^{1/(1-\beta )}}}{\lambda (1-\beta )} \end{align} }[/math]

Crow Bounds

Step 1: Calculate [math]\displaystyle{ {{\lambda }_{c}}(T)=\tfrac{1}{MTB{{F}_{c}}} }[/math] .

Step 2: Use the equations from 5.2.8.2 to calculate the bounds on time given the cumulative failure intensity.

Bounds on Time Given Instantaneous MTBF

Fisher Matrix Bounds

The time, [math]\displaystyle{ T }[/math] , must be positive, thus [math]\displaystyle{ \ln T }[/math] is treated as being normally distributed.

[math]\displaystyle{ \frac{\ln \hat{T}-\ln T}{\sqrt{Var(\ln \hat{T}})}\ \tilde{\ }\ N(0,1) }[/math]

Confidence bounds on the time are given by:

[math]\displaystyle{ CB=\hat{T}{{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\hat{T})}/\hat{T}}} }[/math]

where:

[math]\displaystyle{ \begin{align} & Var(\hat{T})= & {{\left( \frac{\partial T}{\partial \beta } \right)}^{2}}Var(\hat{\beta })+{{\left( \frac{\partial T}{\partial \lambda } \right)}^{2}}Var(\hat{\lambda }) \\ & & +2\left( \frac{\partial T}{\partial \beta } \right)\left( \frac{\partial T}{\partial \lambda } \right)cov(\hat{\beta },\,\,\,\hat{\lambda }) \end{align} }[/math]

The variance calculation is the same as Eqn. (variance1) and:

[math]\displaystyle{ \hat{T}={{(\lambda \beta \cdot MTB{{F}_{i}})}^{1/(1-\beta )}} }[/math]

[math]\displaystyle{ \begin{align} & \frac{\partial T}{\partial \beta }= & {{\left( \lambda \beta \cdot MTB{{F}_{i}} \right)}^{1/(1-\beta )}}\left[ \frac{1}{{{(1-\beta )}^{2}}}\ln (\lambda \beta \cdot MTB{{F}_{i}})+\frac{1}{\beta (1-\beta )} \right] \\ & \frac{\partial T}{\partial \lambda }= & \frac{{{(\lambda \beta \cdot MTB{{F}_{i}})}^{1/(1-\beta )}}}{\lambda (1-\beta )} \end{align} }[/math]

Crow Bounds

Step 1: Calculate the confidence bounds on the instantaneous MTBF as presented in Section 5.5.2.

Step 2: Calculate the bounds on time as follows.

Failure Terminated Data

[math]\displaystyle{ \hat{T}={{(\frac{\lambda \beta \cdot MTB{{F}_{i}}}{c})}^{1/(1-\beta )}} }[/math]

So the lower an upper bounds on time are:

[math]\displaystyle{ {{\hat{T}}_{L}}={{(\frac{\lambda \beta \cdot MTB{{F}_{i}}}{{{c}_{1}}})}^{1/(1-\beta )}} }[/math]

[math]\displaystyle{ {{\hat{T}}_{U}}={{(\frac{\lambda \beta \cdot MTB{{F}_{i}}}{{{c}_{2}}})}^{1/(1-\beta )}} }[/math]

Time Terminated Data

[math]\displaystyle{ \hat{T}={{(\frac{\lambda \beta \cdot MTB{{F}_{i}}}{\Pi })}^{1/(1-\beta )}} }[/math]

So the lower and upper bounds on time are:

[math]\displaystyle{ {{\hat{T}}_{L}}={{(\frac{\lambda \beta \cdot MTB{{F}_{i}}}{{{\Pi }_{1}}})}^{1/(1-\beta )}} }[/math]

[math]\displaystyle{ {{\hat{T}}_{U}}={{(\frac{\lambda \beta \cdot MTB{{F}_{i}}}{{{\Pi }_{2}}})}^{1/(1-\beta )}} }[/math]

Bounds on Time Given Instantaneous Failure Intensity

Fisher Matrix Bounds

The time, [math]\displaystyle{ T }[/math] , must be positive, thus [math]\displaystyle{ \ln T }[/math] is treated as being normally distributed.

[math]\displaystyle{ \frac{\ln \hat{T}-\ln T}{\sqrt{Var(\ln \hat{T}})}\ \tilde{\ }\ N(0,1) }[/math]

Confidence bounds on the time are given by:

[math]\displaystyle{ CB=\hat{T}{{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\hat{T})}/\hat{T}}} }[/math]

where:

[math]\displaystyle{ \begin{align} & Var(\hat{T})= & {{\left( \frac{\partial T}{\partial \beta } \right)}^{2}}Var(\hat{\beta })+{{\left( \frac{\partial T}{\partial \lambda } \right)}^{2}}Var(\hat{\lambda }) \\ & & +2\left( \frac{\partial T}{\partial \beta } \right)\left( \frac{\partial T}{\partial \lambda } \right)cov(\hat{\beta },\,\,\,\hat{\lambda }) \end{align} }[/math]

The variance calculation is the same as Eqn. (variance1) and:

[math]\displaystyle{ \hat{T}={{\left( \frac{{{\lambda }_{i}}(T)}{\lambda \beta } \right)}^{1/(\beta -1)}} }[/math]

[math]\displaystyle{ \begin{align} & \frac{\partial T}{\partial \beta }= & {{\left( \frac{{{\lambda }_{i}}(T)}{\lambda \beta } \right)}^{1/(\beta -1)}}\left[ -\frac{\ln (\tfrac{{{\lambda }_{i}}(T)}{\lambda \beta })}{{{(\beta -1)}^{2}}}+\frac{1}{\beta (1-\beta )} \right] \\ & \frac{\partial T}{\partial \lambda }= & {{\left( \frac{{{\lambda }_{i}}(T)}{\lambda \beta } \right)}^{1/(\beta -1)}}\frac{1}{\lambda (1-\beta )} \end{align} }[/math]

Crow Bounds

Step 1: Calculate [math]\displaystyle{ MTB{{F}_{i}}=\tfrac{1}{{{\lambda }_{i}}(T)} }[/math] .

Step 2: Use the equations from 5.2.10.2 to calculate the bounds on time given the instantaneous failure intensity.

Bounds on Cumulative Number of Failures

Fisher Matrix Bounds

The cumulative number of failures, [math]\displaystyle{ N(t) }[/math] , must be positive, thus [math]\displaystyle{ \ln N(t) }[/math] is treated as being normally distributed.

[math]\displaystyle{ \frac{\ln \hat{N}(t)-\ln N(t)}{\sqrt{Var(\ln \hat{N}(t)})}\ \tilde{\ }\ N(0,1) }[/math]

[math]\displaystyle{ N(t)=\hat{N}(t){{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\hat{N}(t))}/\hat{N}(t)}} }[/math]

where:

[math]\displaystyle{ \hat{N}(t)=\hat{\lambda }{{t}^{{\hat{\beta }}}} }[/math]

[math]\displaystyle{ \begin{align} & Var(\hat{N}(t))= & {{\left( \frac{\partial \hat{N}(t)}{\partial \beta } \right)}^{2}}Var(\hat{\beta })+{{\left( \frac{\partial \hat{N}(t)}{\partial \lambda } \right)}^{2}}Var(\hat{\lambda }) \\ & & +2\left( \frac{\partial \hat{N}(t)}{\partial \beta } \right)\left( \frac{\partial \hat{N}(t)}{\partial \lambda } \right)cov(\hat{\beta },\hat{\lambda }) \end{align} }[/math]

The variance calculation is the same as Eqn. (variance1) and:

[math]\displaystyle{ \begin{align} & \frac{\partial \hat{N}(t)}{\partial \beta }= & \hat{\lambda }{{t}^{{\hat{\beta }}}}\ln t \\ & \frac{\partial \hat{N}(t)}{\partial \lambda }= & {{t}^{{\hat{\beta }}}} \end{align} }[/math]

Crow Bounds

The Crow cumulative number of failure confidence bounds are:

[math]\displaystyle{ \begin{align} & {{N}_{L}}(T)= & \frac{T}{{\hat{\beta }}}{{\lambda }_{i}}{{(T)}_{L}} \\ & {{N}_{U}}(T)= & \frac{T}{{\hat{\beta }}}{{\lambda }_{i}}{{(T)}_{U}} \end{align} }[/math]

where [math]\displaystyle{ {{\lambda }_{i}}{{(T)}_{L}} }[/math] and [math]\displaystyle{ {{\lambda }_{i}}{{(T)}_{U}} }[/math] can be obtained from Eqn. (amsaac14).

Example 2
Calculate the 90% 2-sided confidence bounds on the cumulative and instantaneous failure intensity for the data from Example 1 given in Table 5.1.

Solution Fisher Matrix Bounds
Using [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] estimated in Example 1, Eqns. (lambda2partial), (beta2partial) and (lambdabeta2partial) are:

[math]\displaystyle{ \begin{align} & \frac{{{\partial }^{2}}\Lambda }{\partial {{\lambda }^{2}}}= & -\frac{22}{{{0.4239}^{2}}}=-122.43 \\ & \frac{{{\partial }^{2}}\Lambda }{\partial {{\beta }^{2}}}= & -\frac{22}{{{0.6142}^{2}}}-0.4239\cdot {{620}^{0.6142}}{{(\ln 620)}^{2}}=-967.68 \\ & \frac{{{\partial }^{2}}\Lambda }{\partial \lambda \partial \beta }= & -{{620}^{0.6142}}\ln 620=-333.64 \end{align} }[/math]

The Fisher Matrix then becomes:

For [math]\displaystyle{ T=620 }[/math] hr, the partial derivatives of the cumulative and instantaneous failure intensities are:

[math]\displaystyle{ \begin{align} & \frac{\partial {{\lambda }_{c}}(T)}{\partial \beta }= & \widehat{\lambda }{{T}^{\widehat{\beta }-1}}\ln (T) \\ & = & 0.4239\cdot {{620}^{-0.3858}}\ln 620 \\ & = & 0.22811336 \\ & \frac{\partial {{\lambda }_{c}}(T)}{\partial \lambda }= & {{T}^{\widehat{\beta }-1}} \\ & = & {{620}^{-0.3858}} \\ & = & 0.083694185 \end{align} }[/math]

[math]\displaystyle{ \begin{align} & \frac{\partial {{\lambda }_{i}}(T)}{\partial \beta }= & \widehat{\lambda }{{T}^{\widehat{\beta }-1}}+\widehat{\lambda }\widehat{\beta }{{T}^{\widehat{\beta }-1}}\ln T \\ & = & 0.4239\cdot {{620}^{-0.3858}}+0.4239\cdot 0.6142\cdot {{620}^{-0.3858}}\ln 620 \\ & = & 0.17558519 \end{align} }[/math]

[math]\displaystyle{ \begin{align} & \frac{\partial {{\lambda }_{i}}(T)}{\partial \lambda }= & \widehat{\beta }{{T}^{\widehat{\beta }-1}} \\ & = & 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.051404969 \end{align} }[/math]

Therefore, the variances become:

The cumulative and instantaneous failure intensities at [math]\displaystyle{ T=620 }[/math] hr are:

[math]\displaystyle{ \begin{align} & {{\lambda }_{c}}(T)= & 0.03548 \\ & {{\lambda }_{i}}(T)= & 0.02179 \end{align} }[/math]

So, at the 90% confidence level and for [math]\displaystyle{ T=620 }[/math] hr, the Fisher Matrix confidence bounds for the cumulative failure intensity are:

[math]\displaystyle{ \begin{align} & {{[{{\lambda }_{c}}(T)]}_{L}}= & 0.02499 \\ & {{[{{\lambda }_{c}}(T)]}_{U}}= & 0.05039 \end{align} }[/math]

The confidence bounds for the instantaneous failure intensity are:

[math]\displaystyle{ \begin{align} & {{[{{\lambda }_{i}}(T)]}_{L}}= & 0.01327 \\ & {{[{{\lambda }_{i}}(T)]}_{U}}= & 0.03579 \end{align} }[/math]

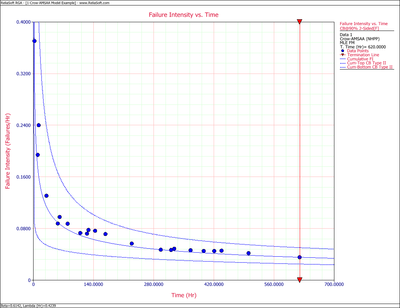
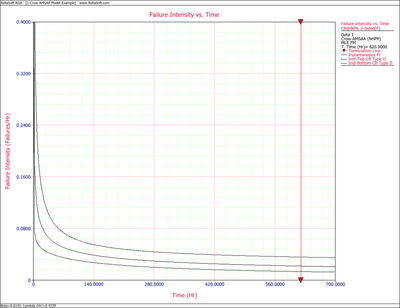
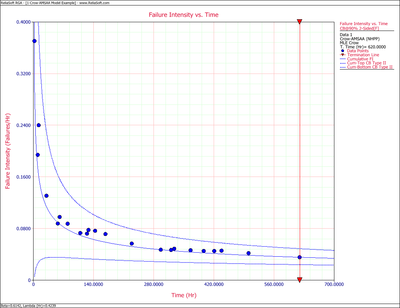
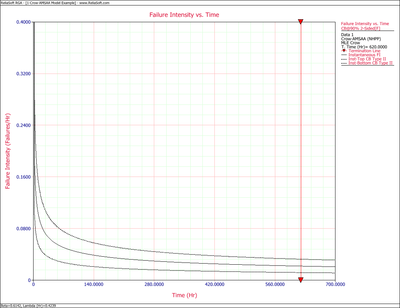
Figures 4fig82 and 4fig83 display plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous failure intensity, respectively.

Cumulative failure intensity with 2-sided 90% Fisher Matrix confidence bounds.

Instantaneous failure intensity with 2-sided 90% Fisher Matrix confidence bounds.

Crow Bounds
The Crow confidence bounds for the cumulative failure intensity at the 90% confidence level and for [math]\displaystyle{ T=620 }[/math] hr are:

[math]\displaystyle{ \begin{align} & {{[{{\lambda }_{c}}(T)]}_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot t} \\ & = & \frac{29.787476}{2*620} \\ & = & 0.02402 \\ & {{[{{\lambda }_{c}}(T)]}_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot t} \\ & = & \frac{62.8296}{2*620} \\ & = & 0.05067 \end{align} }[/math]

The Crow confidence bounds for the instantaneous failure intensity at the 90% confidence level and for [math]\displaystyle{ T=620 }[/math] hr are:

[math]\displaystyle{ \begin{align} & {{[{{\lambda }_{i}}(t)]}_{L}}= & \frac{1}{{{[MTB{{F}_{i}}]}_{U}}} \\ & = & \frac{1}{MTB{{F}_{i}}\cdot U} \\ & = & 0.01179 \end{align} }[/math]

[math]\displaystyle{ \begin{align} & {{[{{\lambda }_{i}}(t)]}_{U}}= & \frac{1}{{{[MTB{{F}_{i}}]}_{L}}} \\ & = & \frac{1}{MTB{{F}_{i}}\cdot L} \\ & = & 0.03253 \end{align} }[/math]

Figures 4fig84 and 4fig85 display plots of the Crow confidence bounds for the cumulative and instantaneous failure intensity, respectively.

Cumulative failure intensity with 2-sided 90% Crow confidence bounds.

Instantaneous failure intensity with 2-sided 90% Crow confidence bounds.

[math]\displaystyle{ \begin{align} & Var(\widehat{\lambda })= & 0.13519969 \\ & Var(\widehat{\beta })= & 0.017105343 \\ & Cov(\widehat{\beta },\widehat{\lambda })= & -0.046614609 \end{align} }[/math]

Example 3
Calculate the confidence bounds on the cumulative and instantaneous MTBF for the data in Table 5.1.
Solution
Fisher Matrix Bounds
From the previous example:

And for [math]\displaystyle{ T=620 }[/math] hr, the partial derivatives of the cumulative and instantaneous MTBF are:

[math]\displaystyle{ \begin{align} & \frac{\partial {{m}_{c}}(T)}{\partial \beta }= & -\frac{1}{\widehat{\lambda }}{{T}^{1-\widehat{\beta }}}\ln T \\ & = & -\frac{1}{0.4239}{{620}^{0.3858}}\ln 620 \\ & = & -181.23135 \\ & \frac{\partial {{m}_{c}}(T)}{\partial \lambda }= & -\frac{1}{{{\widehat{\lambda }}^{2}}}{{T}^{1-\widehat{\beta }}} \\ & = & -\frac{1}{{{0.4239}^{2}}}{{620}^{0.3858}} \\ & = & -66.493299 \\ & \frac{\partial {{m}_{i}}(T)}{\partial \beta }= & -\frac{1}{\widehat{\lambda }{{\widehat{\beta }}^{2}}}{{T}^{1-\beta }}-\frac{1}{\widehat{\lambda }\widehat{\beta }}{{T}^{1-\widehat{\beta }}}\ln T \\ & = & -\frac{1}{0.4239\cdot {{0.6142}^{2}}}{{620}^{0.3858}}-\frac{1}{0.4239\cdot 0.6142}{{620}^{0.3858}}\ln 620 \\ & = & -369.78634 \\ & \frac{\partial {{m}_{i}}(T)}{\partial \lambda }= & -\frac{1}{{{\widehat{\lambda }}^{2}}\widehat{\beta }}{{T}^{1-\widehat{\beta }}} \\ & = & -\frac{1}{{{0.4239}^{2}}\cdot 0.6142}\cdot {{620}^{0.3858}} \\ & = & -108.26001 \end{align} }[/math]

Therefore, the variances become:

[math]\displaystyle{ \begin{align} & Var({{\widehat{m}}_{c}}(T))= & {{\left( -181.23135 \right)}^{2}}\cdot 0.017105343+{{\left( -66.493299 \right)}^{2}}\cdot 0.13519969 \\ & & -2\cdot \left( -181.23135 \right)\cdot \left( -66.493299 \right)\cdot 0.046614609 \\ & = & 36.113376 \end{align} }[/math]

[math]\displaystyle{ \begin{align} & Var({{\widehat{m}}_{i}}(T))= & {{\left( -369.78634 \right)}^{2}}\cdot 0.017105343+{{\left( -108.26001 \right)}^{2}}\cdot 0.13519969 \\ & & -2\cdot \left( -369.78634 \right)\cdot \left( -108.26001 \right)\cdot 0.046614609 \\ & = & 191.33709 \end{align} }[/math]

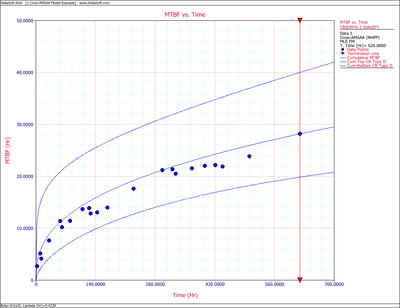
So, at 90% confidence level and [math]\displaystyle{ T=620 }[/math] hr, the Fisher Matrix confidence bounds are:

[math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha }}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 19.84581 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha }}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 40.01927 \end{align} }[/math]

[math]\displaystyle{ \begin{align} & {{[{{m}_{i}}(T)]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha }}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 27.94261 \\ & {{[{{m}_{i}}(T)]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha }}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 75.34193 \end{align} }[/math]

Figures 4fig86 and 4fig87 show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBFs.

Cumulative MTBF with 2-sided 90% Fisher Matrix confidence bounds.

Instantaneous MTBF with 2-sided Fisher Matrix confidence bounds.

Crow Bounds
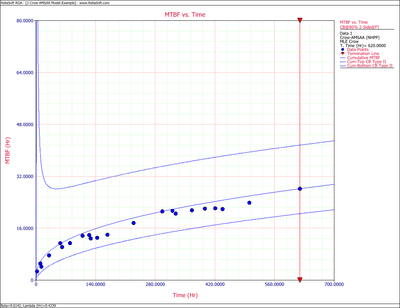
The Crow confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% confidence level and for [math]\displaystyle{ T=620 }[/math] hr are:

[math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{{{[{{\lambda }_{c}}(T)]}_{U}}} \\ & = & 20.5023 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{{{[{{\lambda }_{c}}(T)]}_{L}}} \\ & = & 41.6282 \end{align} }[/math]

[math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & MTB{{F}_{i}}\cdot {{\Pi }_{1}} \\ & = & 30.7445 \\ & {{[MTB{{F}_{i}}]}_{U}}= & MTB{{F}_{i}}\cdot {{\Pi }_{2}} \\ & = & 84.7972 \end{align} }[/math]

Figures 4fig88 and 4fig89 show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.

Cumulative MTBF with 2-sided 90% Crow confidence bounds.

Instantaneous MTBF with 2-sided 90% Crow confidence bounds.

Confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] . For Fisher Matrix confidence bounds:

[math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.4325 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.8722 \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.1016 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.7691 \end{align} }[/math]

For Crow confidence bounds:

[math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & 0.4527 \\ & {{\beta }_{U}}= & 0.9350 \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & 0.2870 \\ & {{\lambda }_{U}}= & 0.5827 \end{align} }[/math]