Weibull Distribution RRX Example: Difference between revisions
Chris Kahn (talk | contribs) |
Chris Kahn (talk | contribs) No edit summary |
||
| Line 3: | Line 3: | ||
</noinclude> | </noinclude> | ||
Assume that 6 identical units are being tested. The failure times are: 93, 34, 16, 120, 53 and 75. What is the unreliability of the units for a mission duration of 30 hours, starting the mission at age zero? To replicate the results in this reference with Weibull++, choose RRX (Rank Regression on X) as the calculation method. | Assume that 6 identical units are being tested. The failure times are: 93, 34, 16, 120, 53 and 75. | ||
1. What is the unreliability of the units for a mission duration of 30 hours, starting the mission at age zero? (To replicate the results in this reference with Weibull++, choose RRX (Rank Regression on X) as the calculation method.) | |||
2. What is the reliability for a new mission of t = 10 hours duration, starting the new mission at the age of T = 30 hours? | |||
3. What is the longest mission that this equipment should undertake for a reliability of 90%? | |||
'''Solution''' | '''Solution''' | ||
First, we use Weibull++ to obtain the parameters using RRX. | 1. First, we use Weibull++ to obtain the parameters using RRX. | ||
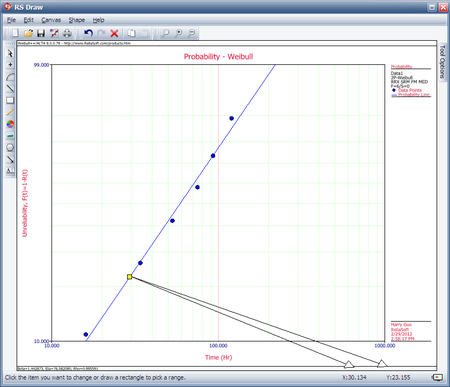
Then, we investigate several methods of solution for this problem. The first, and more laborious, method is to extract the information directly from the plot. You may do this with either the screen plot in RS Draw or the printed copy of the plot. (When extracting information from the screen plot in '''RS Draw''', note that the translated axis position of your mouse is always shown on the bottom right corner.) | Then, we investigate several methods of solution for this problem. The first, and more laborious, method is to extract the information directly from the plot. You may do this with either the screen plot in RS Draw or the printed copy of the plot. (When extracting information from the screen plot in '''RS Draw''', note that the translated axis position of your mouse is always shown on the bottom right corner.) | ||
| Line 22: | Line 28: | ||
Note that the results in QCP vary according to the parameter estimation method used. The above results are obtained using RRX. | Note that the results in QCP vary according to the parameter estimation method used. The above results are obtained using RRX. | ||
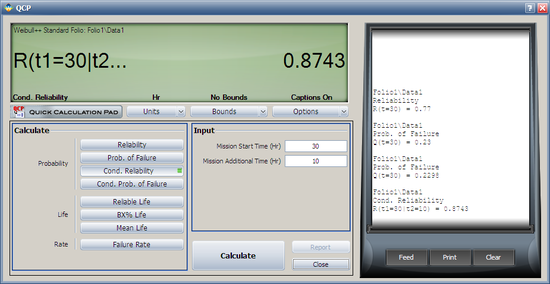
2. The conditional reliability is given by: | |||
::<math>R(t|T)=\frac{R(T+t)}{R(T)}</math> | |||
or: | |||
::<math>\hat{R}(10hr|30hr)=\frac{\hat{R}(10+30)}{\hat{R}(30)}=\frac{\hat{R}(40)}{\hat{R}(30)}</math> | |||
Again, the '''Quick Calculation Pad''' can provide this result directly and more accurately than the plot. | |||
[[Image: Conditional R.png|center|550px]] | |||
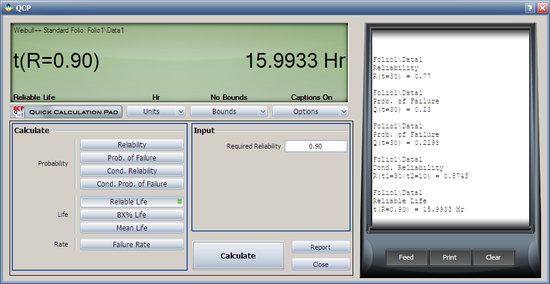
3. Using the '''QCP''' again, choose '''Reliable Life''' and enter the Required Reliability, 0.90, and click '''Calculate'''. The result is 15.9933 hours. | |||
[[Image: Reliable Life.png|center|550px]] | |||
Revision as of 01:11, 23 August 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This examples also appears in the Life Data Analysis Reference book.
Assume that 6 identical units are being tested. The failure times are: 93, 34, 16, 120, 53 and 75.
1. What is the unreliability of the units for a mission duration of 30 hours, starting the mission at age zero? (To replicate the results in this reference with Weibull++, choose RRX (Rank Regression on X) as the calculation method.)
2. What is the reliability for a new mission of t = 10 hours duration, starting the new mission at the age of T = 30 hours?
3. What is the longest mission that this equipment should undertake for a reliability of 90%?
Solution
1. First, we use Weibull++ to obtain the parameters using RRX.
Then, we investigate several methods of solution for this problem. The first, and more laborious, method is to extract the information directly from the plot. You may do this with either the screen plot in RS Draw or the printed copy of the plot. (When extracting information from the screen plot in RS Draw, note that the translated axis position of your mouse is always shown on the bottom right corner.)
Using this first method, enter either the screen plot or the printed plot with T = 30 hours, go up vertically to the straight line fitted to the data, then go horizontally to the ordinate, and read off . Then, a good estimate of the sought unreliability is 23%. (Also, the reliability estimate is 1.0 - 0.23 = 0.77 or 77%.)
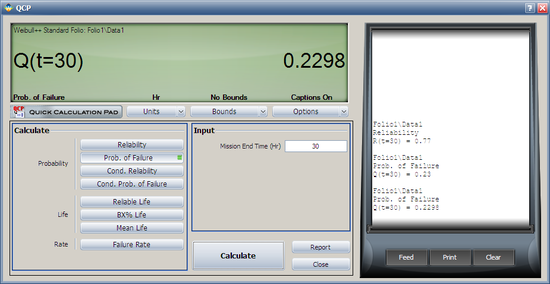
The second method involves the use of the Quick Calculation Pad (QCP).
Select Prob. of Failure calculation option and enter 30 hours in the Mission End Time box. Click Calculate to get the result.
Note that the results in QCP vary according to the parameter estimation method used. The above results are obtained using RRX.
2. The conditional reliability is given by:
- [math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)} }[/math]
or:
- [math]\displaystyle{ \hat{R}(10hr|30hr)=\frac{\hat{R}(10+30)}{\hat{R}(30)}=\frac{\hat{R}(40)}{\hat{R}(30)} }[/math]
Again, the Quick Calculation Pad can provide this result directly and more accurately than the plot.
3. Using the QCP again, choose Reliable Life and enter the Required Reliability, 0.90, and click Calculate. The result is 15.9933 hours.