Inverse Power Law Example: Difference between revisions
Jump to navigation
Jump to search
Lisa Hacker (talk | contribs) No edit summary |
No edit summary |
||
| Line 11: | Line 11: | ||
The data set was analyzed jointly in an ALTA standard folio using the IPL-Weibull model, with a complete MLE solution over the entire data set. The analysis yields: | The data set was analyzed jointly in an ALTA standard folio using the IPL-Weibull model, with a complete MLE solution over the entire data set. The analysis yields: | ||
::<math>\widehat{\beta }=2.616464</math> | ::<math>\widehat{\beta }=2.616464\,\!</math> | ||
::<math>\widehat{K}=0.001022</math> | ::<math>\widehat{K}=0.001022\,\!</math> | ||
::<math>\widehat{n}=1.327292</math> | ::<math>\widehat{n}=1.327292\,\!</math> | ||
Revision as of 21:48, 21 September 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.
This example appears in the Accelerated Life Testing Data Analysis Reference book.
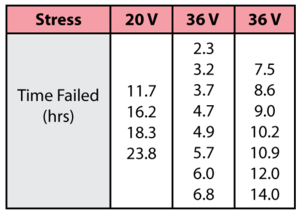
Consider the following times-to-failure data at two different stress levels.
The data set was analyzed jointly in an ALTA standard folio using the IPL-Weibull model, with a complete MLE solution over the entire data set. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=2.616464\,\! }[/math]
- [math]\displaystyle{ \widehat{K}=0.001022\,\! }[/math]
- [math]\displaystyle{ \widehat{n}=1.327292\,\! }[/math]