Exponential Chi-Squared Example: Difference between revisions
Lisa Hacker (talk | contribs) (Created page with '<noinclude>{{Banner Weibull Examples}} ''This example appears in the Life Data Analysis Reference book''. </noinclude> '''Example: Using Exponential …') |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 4: | Line 4: | ||
</noinclude> | </noinclude> | ||
'''Example: Using Exponential Chi-Squared Method''' | '''Example: Using Exponential Chi-Squared Method''' | ||
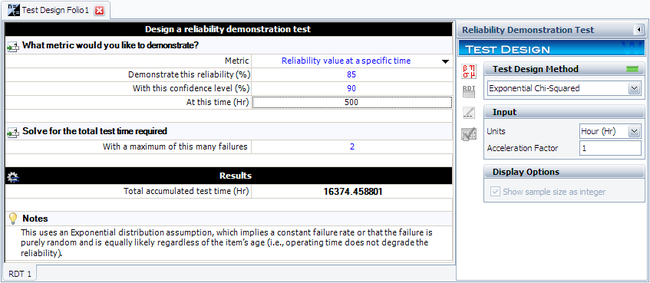
In this example, we desire to design a test to demonstrate a reliability of 85% at <math>{{t}_{DEMO}}=500</math> hours with a 90% confidence, or <math>CL=0.9,</math> and two allowable failures, <math>f=2</math> . The chi-squared value can be determined from tables or the Quick Statistical Reference in Weibull++. In this example, the value is calculated as: | In this example, we desire to design a test to demonstrate a reliability of 85% at <math>{{t}_{DEMO}}=500</math> hours with a 90% confidence, or <math>CL=0.9,</math> and two allowable failures, <math>f=2</math> . The chi-squared value can be determined from tables or the Quick Statistical Reference in Weibull++. In this example, the value is calculated as: | ||
Revision as of 03:03, 15 August 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life Data Analysis Reference book.
Example: Using Exponential Chi-Squared Method
In this example, we desire to design a test to demonstrate a reliability of 85% at [math]\displaystyle{ {{t}_{DEMO}}=500 }[/math] hours with a 90% confidence, or [math]\displaystyle{ CL=0.9, }[/math] and two allowable failures, [math]\displaystyle{ f=2 }[/math] . The chi-squared value can be determined from tables or the Quick Statistical Reference in Weibull++. In this example, the value is calculated as:
- [math]\displaystyle{ \chi _{1-CL;2r+2}^{2}=\chi _{0.1;6}^{2}=10.6446 }[/math]
Substituting this into the chi-squared equation, we obtain:
- [math]\displaystyle{ {{T}_{a}}=\frac{\tfrac{500}{-ln(0.85)}\cdot 10.6446}{2}=16,374\text{ hours} }[/math]
This means that 16,374 hours of total test time needs to be accumulated with no more than two failures in order to demonstrate the specified reliability.
This example solved in Weibull++ is shown next.
Given the test time, one can now solve for the number of units using the chi-squared equation. Similarly, if the number of units is given, one can determine the test time from the chi-squared equation for exponential test design.