Mechanical Components Example

Mechanical Components Example

A mechanical component was put into an accelerated test with temperature as the accelerated stress. The following times-to-failure were observed.

343 K	363 K	383 K
266.66	618.54	351.12
430.09	666.72	355.1
570.45	724.4	672.69
890.42	950.89	923.35
1046.65	1148.4	948.22
1158.14	1202.94	1277.04
1396.01	1492.56	1538.81
1918.38	1619.59	2020.34
2028.86	2592.29	2099.03
2785.58	3596.85	2173.04

1) Determine the parameters of the Arrhenius-Weibull model.

2) What is your observation?

Solution

The parameters of the Arrhenius Weibull model were estimated using ALTA with the following results:

[math]\displaystyle{ \begin{align} \beta =1.771460,\text{ }B=86.183591,\text{ }C=1170.423770. \end{align} }[/math]

A small value for [math]\displaystyle{ B }[/math] was estimated. The following observations can then be made:

• Life is not accelerated with temperature, or

• the stress increments were not sufficient, or

• the test stresses were well within the "specification limits" for the product (see discussion here).

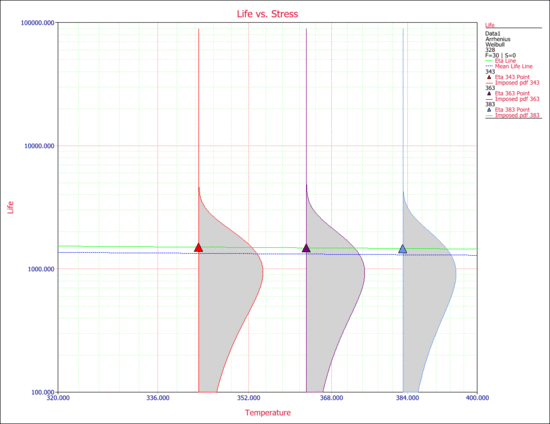
A small value for [math]\displaystyle{ B }[/math] is not the only indication for this behavior. One can also observe from the data that at all three stress levels, the times-to-failure are within the same range. Another way to observe this is by looking at the Arrhenius plot. The scale parameter, [math]\displaystyle{ \eta }[/math] , and the mean life are plotted next.

Eta and Mean Life vs. Stress.

It can be seen that life ( [math]\displaystyle{ \eta }[/math] , and the mean life) is almost invariant with stress.