Stress-Strength Parameter Uncertainty Example: Difference between revisions
No edit summary |
No edit summary |
||
| Line 128: | Line 128: | ||
First, estimate the stress and strength distributions using the given data. Enter the stress and strength data into two separate data sheets and analyze each data sheet using the lognormal distribution and MLE analysis method. The parameters of the stress distribution are estimated to be log-mean = 9.411844 and log-std = 0.098741. | First, estimate the stress and strength distributions using the given data. Enter the stress and strength data into two separate data sheets and analyze each data sheet using the lognormal distribution and MLE analysis method. The parameters of the stress distribution are estimated to be log-mean = 9.411844 and log-std = 0.098741. | ||
[[Image:Stress-Strength Example 1 Stress-Distribution.png|center|550px]] | [[Image:Stress-Strength Example 1 Stress-Distribution.png|center|550px]] | ||
The parameters of the strength distribution are estimated to be log-mean = 9.681503 and log-std = 0.083494. | The parameters of the strength distribution are estimated to be log-mean = 9.681503 and log-std = 0.083494. | ||
[[Image:Stress-Strength Example 1 Strength-Distribution.png|center|550px]] | [[Image:Stress-Strength Example 1 Strength-Distribution.png|center|550px]] | ||
Next, open the Stress-Strength tool and choose to compare the two data sheets. The following picture shows the ''pdf'' curves of the two data sets: | Next, open the Stress-Strength tool and choose to compare the two data sheets. The following picture shows the ''pdf'' curves of the two data sets: | ||
[[Image:Stress-Strength Example 1 pdf curve.png|center|550px]] | [[Image:Stress-Strength Example 1 pdf curve.png|center|550px]] | ||
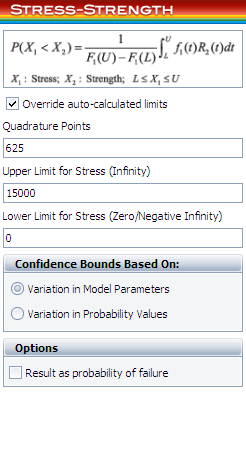
Since the warranty is 1 year/15,000 miles, all the vehicles with mileage larger than 15,000 should not be considered in the calculation. To do this, go to the Setup page of the control panel and select the '''Override auto-calculated limits''' check box. Set the value of the upper limit to '''15,000''' as shown next. | Since the warranty is 1 year/15,000 miles, all the vehicles with mileage larger than 15,000 should not be considered in the calculation. To do this, go to the Setup page of the control panel and select the '''Override auto-calculated limits''' check box. Set the value of the upper limit to '''15,000''' as shown next. | ||
[[Image:Stress-Strength Example 1 Calculation Settings.png|center|250px]] | |||
[[Image:Stress-Strength Example 1 Calculation Settings.png|center| | |||
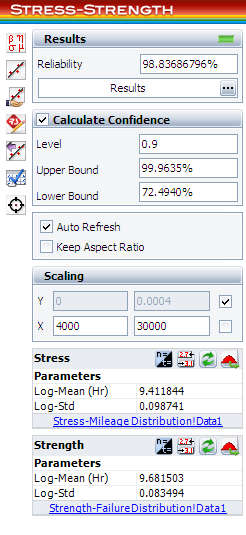
Recalculate the results. The estimated reliability for vehicles less than 15,000 miles per year is 98.84%. The associated confidence bounds are estimated from the variance of the distribution parameters. With larger samples for the stress and strength data, the width of the bounds will be narrower. | Recalculate the results. The estimated reliability for vehicles less than 15,000 miles per year is 98.84%. The associated confidence bounds are estimated from the variance of the distribution parameters. With larger samples for the stress and strength data, the width of the bounds will be narrower. | ||
[[Image:Stress-Strength Example 1 Calculation Results.png|center| | [[Image:Stress-Strength Example 1 Calculation Results.png|center|250px]] | ||
Revision as of 05:52, 6 August 2012
 |
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life Data Analysis Reference book.
Assume that we are going to use stress-strength analysis to estimate the reliability of a component used in a vehicle. The stress is the usage mileage distribution and the strength is the miles-to-failure distribution of the component. The warranty is 1 year or 15,000 miles, whichever is earlier. The goal is to estimate the reliability of the component within the warranty period (1 year/15,000 miles).
The following table gives the data for the mileage distribution per year (stress):
| Stress: Usage Mileage Distribution | |
| 10096 | 12405 |
| 10469 | 12527 |
| 10955 | 12536 |
| 11183 | 12595 |
| 11391 | 12657 |
| 11486 | 13777 |
| 11534 | 13862 |
| 11919 | 13971 |
| 12105 | 14032 |
| 12141 | 14138 |
The following table gives the data for the miles-to-failure distribution (strength):
| Strength: Failure Mileage Distribution | |
| 13507 | 16125 |
| 13793 | 16320 |
| 13943 | 16327 |
| 14017 | 16349 |
| 14147 | 16406 |
| 14351 | 16501 |
| 14376 | 16611 |
| 14595 | 16625 |
| 14746 | 16670 |
| 14810 | 16749 |
| 14940 | 16793 |
| 14951 | 16862 |
| 15104 | 16930 |
| 15218 | 16948 |
| 15303 | 17024 |
| 15311 | 17041 |
| 15480 | 17263 |
| 15496 | 17347 |
| 15522 | 17430 |
| 15547 | 17805 |
| 15570 | 17884 |
| 15975 | 18549 |
| 16003 | 18575 |
| 16018 | 18813 |
| 16052 | 18944 |
Solution
First, estimate the stress and strength distributions using the given data. Enter the stress and strength data into two separate data sheets and analyze each data sheet using the lognormal distribution and MLE analysis method. The parameters of the stress distribution are estimated to be log-mean = 9.411844 and log-std = 0.098741.
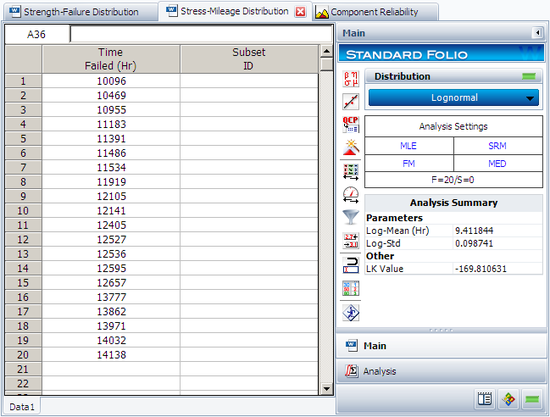
The parameters of the strength distribution are estimated to be log-mean = 9.681503 and log-std = 0.083494.
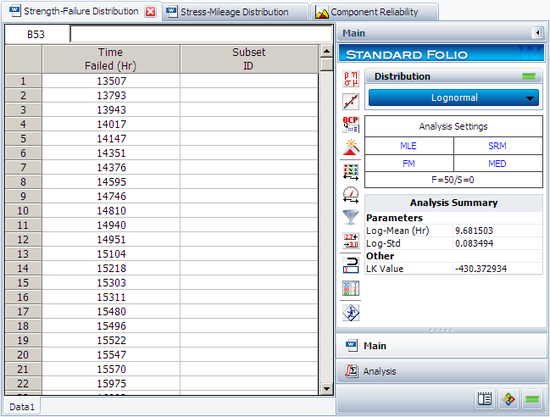
Next, open the Stress-Strength tool and choose to compare the two data sheets. The following picture shows the pdf curves of the two data sets:
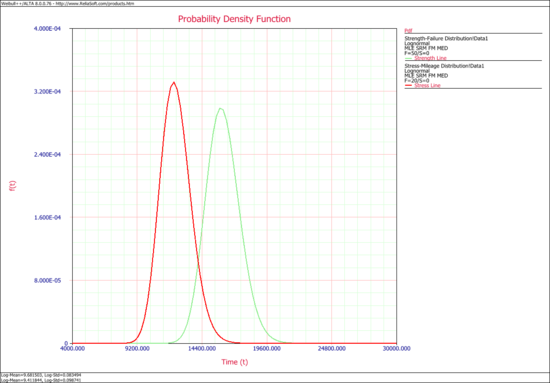
Since the warranty is 1 year/15,000 miles, all the vehicles with mileage larger than 15,000 should not be considered in the calculation. To do this, go to the Setup page of the control panel and select the Override auto-calculated limits check box. Set the value of the upper limit to 15,000 as shown next.
Recalculate the results. The estimated reliability for vehicles less than 15,000 miles per year is 98.84%. The associated confidence bounds are estimated from the variance of the distribution parameters. With larger samples for the stress and strength data, the width of the bounds will be narrower.