Template:Example: Weibull Disribution Conditional Reliability RRX Example: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
'''Weibull | '''Weibull Distribution Conditional Reliability RRX Example''' | ||
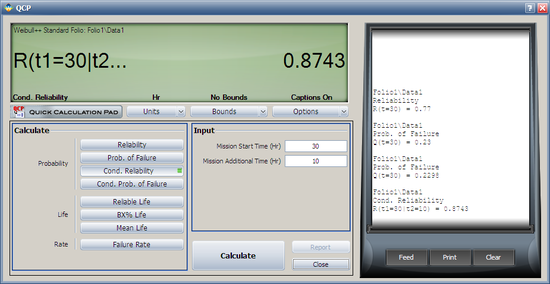
What is the reliability for a new mission of t = 10 hours duration, starting the new mission at the age of T = 30 hours, for the same data as [[Example: Weibull Disribution Unreliability RRX Example|Example 8]]? | What is the reliability for a new mission of t = 10 hours duration, starting the new mission at the age of T = 30 hours, for the same data as [[Example: Weibull Disribution Unreliability RRX Example|Example 8]]? | ||
Revision as of 09:19, 8 August 2012
Weibull Distribution Conditional Reliability RRX Example
What is the reliability for a new mission of t = 10 hours duration, starting the new mission at the age of T = 30 hours, for the same data as Example 8?
Solution
The conditional reliability is given by:
- [math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)} }[/math]
or:
- [math]\displaystyle{ \hat{R}(10hr|30hr)=\frac{\hat{R}(10+30)}{\hat{R}(30)}=\frac{\hat{R}(40)}{\hat{R}(30)} }[/math]
Again, the Quick Calculation Pad can provide this result directly and more accurately than the plot.