Template:Example: Weibull Disribution Conditional Reliability RRX Example: Difference between revisions
Jump to navigation
Jump to search
[math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)} }[/math]
[math]\displaystyle{ \hat{R}(10hr|30hr)=\frac{\hat{R}(10+30)}{\hat{R}(30)}=\frac{\hat{R}(40)}{\hat{R}(30)} }[/math]
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
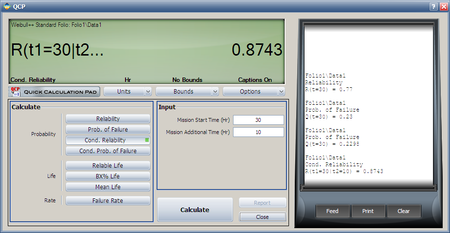
What is the reliability for a new mission of t = 10 hours duration, starting the new mission at the age of T = 30 hours, for the same data as [[Example: Weibull Disribution Unreliability RRX Example|Example 8]]? | What is the reliability for a new mission of t = 10 hours duration, starting the new mission at the age of T = 30 hours, for the same data as [[Example: Weibull Disribution Unreliability RRX Example|Example 8]]? | ||
'''Solution''' | '''Solution''' | ||
Revision as of 05:12, 6 August 2012
Weibull Disribution Conditional Reliability RRX Example
What is the reliability for a new mission of t = 10 hours duration, starting the new mission at the age of T = 30 hours, for the same data as Example 8?
Solution
The conditional reliability is given by:
or:
Again, the Quick Calculation Pad can provide this result directly and more accurately than the plot.