Non-Parametric RDA Transmission Example: Difference between revisions
Kate Racaza (talk | contribs) m (moved Template:Example: Recurrent Events Data Non-parameteric Transmission Example to Non-Parametric RDA Transmission Example: incorrect namespace and misspelled title.) |
Kate Racaza (talk | contribs) (updated example) |
||
| Line 1: | Line 1: | ||
'' | <noinclude>{{Banner Weibull Examples}} | ||
''This example appears in the [[Recurrent_Event_Data_Analysis#Non-Parametric_Recurrent_Event_Data_Analysis|Life Data Analysis Reference book]]''. | |||
</noinclude>'''Transmission Example''' | |||
The following table shows the repairs in a pre-production road test on a sample of 14 cars with manual transmissions [[Appendix: Weibull References|[31]]]. Here, the + sign denotes the censoring ages (how long a car has been observed). | |||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
Car ID & Mileage \\ | Car ID & Mileage \\ | ||
| Line 19: | Line 25: | ||
\text{14} & \text{3240, 7690, 18965+} \\ | \text{14} & \text{3240, 7690, 18965+} \\ | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
The car manufacturer seeks to estimate the mean cumulative number of repairs per car by 24,000 test miles (equivalently 5.5 x 24,000 = 132,000 customer miles) and to observe whether the population repair rate increases or decreases as | |||
The car manufacturer seeks to estimate the mean cumulative number of repairs per car by 24,000 test miles (equivalently 5.5 x 24,000 = 132,000 customer miles) and to observe whether the population repair rate increases or decreases as the population ages. | |||
<br>'''Solution''' | <br>'''Solution''' | ||
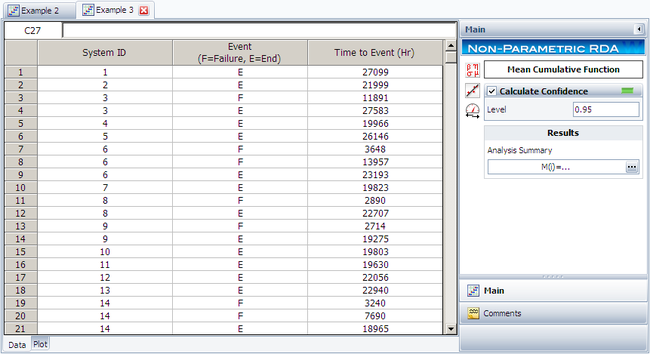
Enter the data into a non-parametric RDA folio in Weibull++, as follows. | |||
[[Image:Recurrent Data Example 3 Data.png|center|650px]] | |||
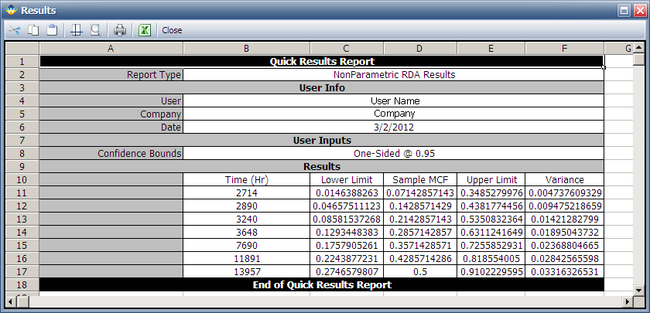
The results are as follows. | |||
[[Image:Recurrent Data Example 3 Result.png|center|650px]] | |||
The results indicate that after 13,957 miles of testing, the estimated mean cumulative number of repairs per car is 0.5. Therefore, by 24,000 test miles, the estimated mean cumulative number of repairs per car is 0.5. | The results indicate that after 13,957 miles of testing, the estimated mean cumulative number of repairs per car is 0.5. Therefore, by 24,000 test miles, the estimated mean cumulative number of repairs per car is 0.5. | ||
| Line 35: | Line 47: | ||
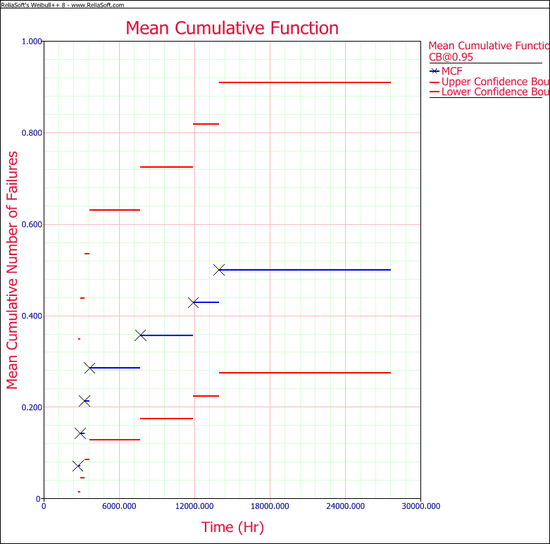
The MCF plot is shown next. | The MCF plot is shown next. | ||
[[Image:Recurrent Data Example 3 Plot.png | |||
[[Image:Recurrent Data Example 3 Plot.png|center|550px]] | |||
A smooth curve through the MCF plot has a derivative that decreases as the population ages. That is, the repair rate decreases as each population ages. This is typical of products with manufacturing defects. | A smooth curve through the MCF plot has a derivative that decreases as the population ages. That is, the repair rate decreases as each population ages. This is typical of products with manufacturing defects. | ||
Revision as of 03:47, 1 August 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life Data Analysis Reference book.
Transmission Example
The following table shows the repairs in a pre-production road test on a sample of 14 cars with manual transmissions [31]. Here, the + sign denotes the censoring ages (how long a car has been observed).
The car manufacturer seeks to estimate the mean cumulative number of repairs per car by 24,000 test miles (equivalently 5.5 x 24,000 = 132,000 customer miles) and to observe whether the population repair rate increases or decreases as the population ages.
Solution
Enter the data into a non-parametric RDA folio in Weibull++, as follows.
The results are as follows.
The results indicate that after 13,957 miles of testing, the estimated mean cumulative number of repairs per car is 0.5. Therefore, by 24,000 test miles, the estimated mean cumulative number of repairs per car is 0.5.
The MCF plot is shown next.
A smooth curve through the MCF plot has a derivative that decreases as the population ages. That is, the repair rate decreases as each population ages. This is typical of products with manufacturing defects.