Tensile Components Example: Difference between revisions
Chris Kahn (talk | contribs) |
No edit summary |
||
| Line 1: | Line 1: | ||
===Tensile Components Example=== | ===Tensile Components Example=== | ||
A tensile component of a landing gear was put through an accelerated reliability test to determine whether the life goal would be achieved under the designed-in load. Fifteen units, N=15, were tested at three different shock loads. The component was designed for a peak shock load of 50 kips with an estimated return of 10% of the population by 10,000 landings. Using the inverse power law lognormal model, determine whether the design life was met. | A tensile component of a landing gear was put through an accelerated reliability test to determine whether the life goal would be achieved under the designed-in load. Fifteen units, N=15, were tested at three different shock loads. The component was designed for a peak shock load of 50 kips with an estimated return of 10% of the population by 10,000 landings. Using the inverse power law lognormal model, determine whether the design life was met. | ||
{|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | |||
{| | |||
!Failure, in Cycles | !Failure, in Cycles | ||
!Shock Load, kips | !Shock Load, kips | ||
| Line 39: | Line 37: | ||
|216|| 128 | |216|| 128 | ||
|} | |} | ||
====Solution==== | ====Solution==== | ||
The data were entered into ALTA, and the following estimates were obtained for the parameters of the IPL-lognormal model: | The data were entered into ALTA, and the following estimates were obtained for the parameters of the IPL-lognormal model: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 56: | Line 52: | ||
\end{align}</math> | \end{align}</math> | ||
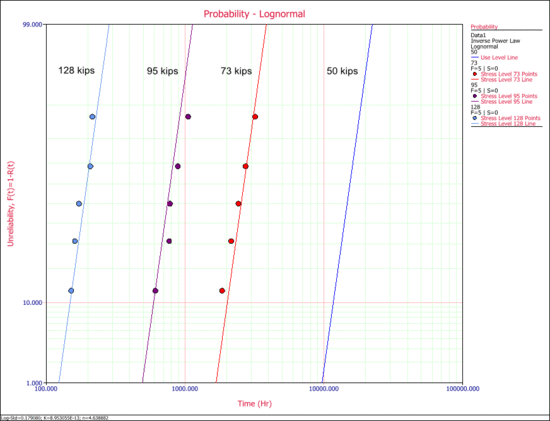
The probability plot at each test stress level (73 kips, 95 kips and 123 kips) was then obtained, as shown next. | The probability plot at each test stress level (73 kips, 95 kips and 123 kips) was then obtained, as shown next. | ||
[[Image:new_3.gif|thumb|center|550px|Probability plots at different shock loads.]] | |||
[[Image:new_3.gif|thumb|center| | |||
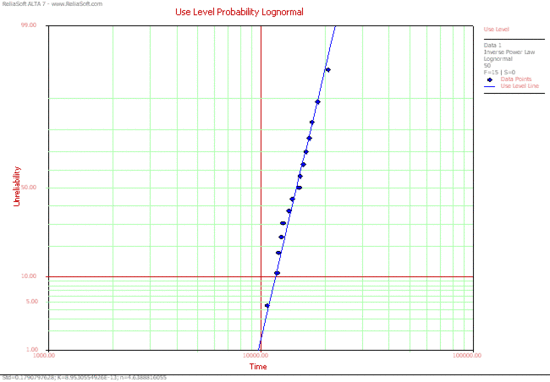
In this plot, it can be seen that there is a good agreement between the data and the fitted model. The probability plot at a use stress level of 50 kips is shown next. | In this plot, it can be seen that there is a good agreement between the data and the fitted model. The probability plot at a use stress level of 50 kips is shown next. | ||
[[Image:new_4.gif|thumb|center|550px|The probability plot at a use stress level of 50 kips.]] | |||
[[Image:new_4.gif|thumb|center| | |||
Using the Use Level Probability plot, the cycles-to failure for a 10% probability of failure can be estimated. From the plot, this time is estimated to be <math>T(Q=0.10=10%)\approxeq 12,000</math> landings. | Using the Use Level Probability plot, the cycles-to failure for a 10% probability of failure can be estimated. From the plot, this time is estimated to be <math>T(Q=0.10=10%)\approxeq 12,000</math> landings. | ||
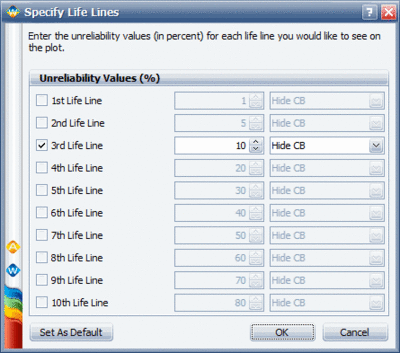
Another way to obtain life information is by using a Life vs. Stress plot. Once a Life vs. Stress plot is selected, the 10% unreliability (probability of failure) line must be plotted. To do this, click Life Lines... in the plot panel and and select the 10% Unreliability box (or enter 10 in one of the boxes and select the box) in the Specify Life Lines window, as shown next. | Another way to obtain life information is by using a Life vs. Stress plot. Once a Life vs. Stress plot is selected, the 10% unreliability (probability of failure) line must be plotted. To do this, click Life Lines... in the plot panel and and select the 10% Unreliability box (or enter 10 in one of the boxes and select the box) in the Specify Life Lines window, as shown next. | ||
[[Image:ipl_example_specify_life.gif|center|400px|]] | |||
[[Image:ipl_example_specify_life.gif | |||
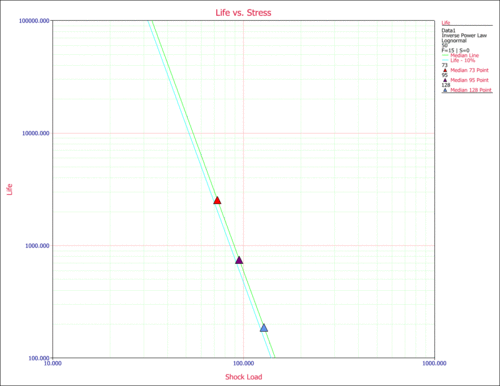
In the following plot, the 10% unreliability line is plotted (the first line from the left). For a stress of 50 psi (X-axis) and for the 10% unreliability line, the cycles-to-failure can be obtained by reading the value on the Y-axis. Again, <math>T(0.1)\approxeq 12,000</math> landings. | In the following plot, the 10% unreliability line is plotted (the first line from the left). For a stress of 50 psi (X-axis) and for the 10% unreliability line, the cycles-to-failure can be obtained by reading the value on the Y-axis. Again, <math>T(0.1)\approxeq 12,000</math> landings. | ||
[[Image:new_5.gif|thumb|center|500px|Median Life line (right) and 10% unreliability line (left) vs. stress.]] | [[Image:new_5.gif|thumb|center|500px|Median Life line (right) and 10% unreliability line (left) vs. stress.]] | ||
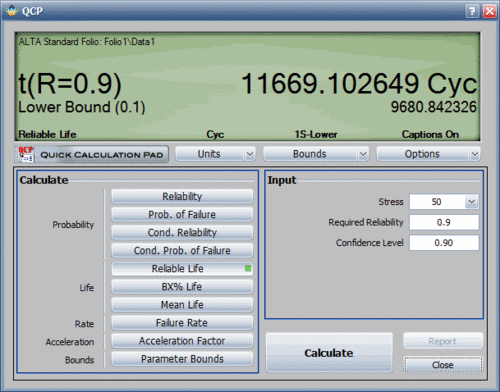
However, a more accurate way to obtain such information is by using the Quick Calculation Pad (QCP) in ALTA. Using the QCP, the life for a 10% probability of failure at 50 kips is estimated to be 11,669.1 cycles (or landings), as shown next. | However, a more accurate way to obtain such information is by using the Quick Calculation Pad (QCP) in ALTA. Using the QCP, the life for a 10% probability of failure at 50 kips is estimated to be 11,669.1 cycles (or landings), as shown next. | ||
[[Image:ipl_example2_qcp.gif|center|500px|]] | |||
[[Image:ipl_example2_qcp.gif | |||
The design criterion of 10,000 landings is met. | The design criterion of 10,000 landings is met. | ||
Revision as of 06:57, 9 August 2012
Tensile Components Example
A tensile component of a landing gear was put through an accelerated reliability test to determine whether the life goal would be achieved under the designed-in load. Fifteen units, N=15, were tested at three different shock loads. The component was designed for a peak shock load of 50 kips with an estimated return of 10% of the population by 10,000 landings. Using the inverse power law lognormal model, determine whether the design life was met.
| Failure, in Cycles | Shock Load, kips |
|---|---|
| 1855 | 73 |
| 2158 | 73 |
| 2425 | 73 |
| 2736 | 73 |
| 3206 | 73 |
| 614 | 95 |
| 770 | 95 |
| 781 | 95 |
| 890 | 95 |
| 1055 | 95 |
| 152 | 128 |
| 162 | 128 |
| 173 | 128 |
| 209 | 128 |
| 216 | 128 |
Solution
The data were entered into ALTA, and the following estimates were obtained for the parameters of the IPL-lognormal model:
- [math]\displaystyle{ \begin{align} Std=\ & 0.179080 \\ K=\ & 8.953055E-13 \\ n=\ & 4.638882 \end{align} }[/math]
The probability plot at each test stress level (73 kips, 95 kips and 123 kips) was then obtained, as shown next.
In this plot, it can be seen that there is a good agreement between the data and the fitted model. The probability plot at a use stress level of 50 kips is shown next.
Using the Use Level Probability plot, the cycles-to failure for a 10% probability of failure can be estimated. From the plot, this time is estimated to be [math]\displaystyle{ T(Q=0.10=10%)\approxeq 12,000 }[/math] landings. Another way to obtain life information is by using a Life vs. Stress plot. Once a Life vs. Stress plot is selected, the 10% unreliability (probability of failure) line must be plotted. To do this, click Life Lines... in the plot panel and and select the 10% Unreliability box (or enter 10 in one of the boxes and select the box) in the Specify Life Lines window, as shown next.
In the following plot, the 10% unreliability line is plotted (the first line from the left). For a stress of 50 psi (X-axis) and for the 10% unreliability line, the cycles-to-failure can be obtained by reading the value on the Y-axis. Again, [math]\displaystyle{ T(0.1)\approxeq 12,000 }[/math] landings.
However, a more accurate way to obtain such information is by using the Quick Calculation Pad (QCP) in ALTA. Using the QCP, the life for a 10% probability of failure at 50 kips is estimated to be 11,669.1 cycles (or landings), as shown next.
The design criterion of 10,000 landings is met.