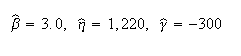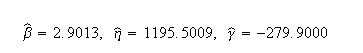Template:Example: Published 3P Weibull Distribution Probability Plot Example: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
'''Published 3P Weibull Distribution Probability Plot Example''' | '''Published 3P Weibull Distribution Probability Plot Example''' | ||
From Dimitri Kececioglu, Reliability & Life Testing Handbook, Page 406. [[Appendix: Weibull References|[20]]]. | From Dimitri Kececioglu, Reliability & Life Testing Handbook, Page 406. [[Appendix: Weibull References|[20]]]. | ||
Estimate the parameters for three-parameter Weibull, for a sample of ten units all tested to failure. The times-to-failure were recorded at 200; 370; 500; 620; 730; 840; 950; 1,050; 1,160; and 1,400 hours. | Estimate the parameters for three-parameter Weibull, for a sample of ten units all tested to failure. The times-to-failure were recorded at 200; 370; 500; 620; 730; 840; 950; 1,050; 1,160; and 1,400 hours. | ||
'''Published Results:''' | '''Published Results:''' | ||
| Line 11: | Line 9: | ||
Published results (using probability plotting): | Published results (using probability plotting): | ||
[[Image:example19formula.png | [[Image:example19formula.png]] | ||
'''Computed Results in Weibull++''' | '''Computed Results in Weibull++''' | ||
| Line 18: | Line 15: | ||
Weibull++ computed parameters for rank regression on X are: | Weibull++ computed parameters for rank regression on X are: | ||
[[Image:compexample19formula.png | [[Image:compexample19formula.png]] | ||
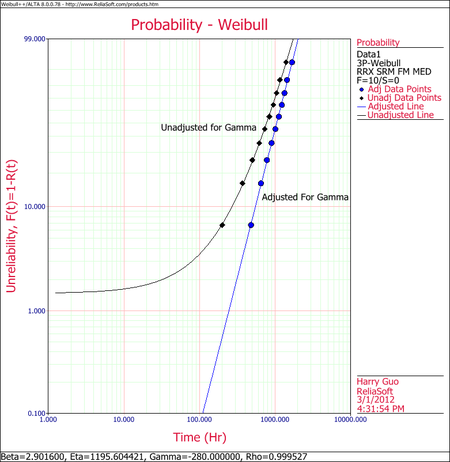
The small difference between the published results and the ones obtained from Weibull++ are due to the difference in the estimation method. In the publication the parameters were estimated using probability plotting (i.e. the fitted line was "eye-balled"). In Weibull++, the parameters were estimated using non-linear regression (a more accurate, mathematically fitted line). Note that γ in this example is negative. This means that the unadjusted for γ line is concave up, as shown next. | The small difference between the published results and the ones obtained from Weibull++ are due to the difference in the estimation method. In the publication the parameters were estimated using probability plotting (i.e. the fitted line was "eye-balled"). In Weibull++, the parameters were estimated using non-linear regression (a more accurate, mathematically fitted line). Note that γ in this example is negative. This means that the unadjusted for γ line is concave up, as shown next. | ||
[[Image:Weibull Distribution Example 19 Plot.png|center|450px]] | |||
[[Image:Weibull Distribution Example 19 Plot.png|center| | |||
Revision as of 05:25, 6 August 2012
Published 3P Weibull Distribution Probability Plot Example
From Dimitri Kececioglu, Reliability & Life Testing Handbook, Page 406. [20].
Estimate the parameters for three-parameter Weibull, for a sample of ten units all tested to failure. The times-to-failure were recorded at 200; 370; 500; 620; 730; 840; 950; 1,050; 1,160; and 1,400 hours.
Published Results:
Published results (using probability plotting):
Computed Results in Weibull++
Weibull++ computed parameters for rank regression on X are:
The small difference between the published results and the ones obtained from Weibull++ are due to the difference in the estimation method. In the publication the parameters were estimated using probability plotting (i.e. the fitted line was "eye-balled"). In Weibull++, the parameters were estimated using non-linear regression (a more accurate, mathematically fitted line). Note that γ in this example is negative. This means that the unadjusted for γ line is concave up, as shown next.