Template:Example: Stress-Strength Analysis with Parameter Uncertainty: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
Line 1: Line 1:
'''Stress-Strength Analysis with Parameter Uncertainty'''
'''Stress-Strength Analysis with Parameter Uncertainty'''  


Assume we are going to use stress-strength analysis to estimate the reliability of a component used in a vehicle. The stress is the usage mileage distribution and the strength is the failure mileage distribution of the component. The warranty is 1 year or 15,000 miles, whichever is earlier. The table below gives the mileage distribution per year.
Assume we are going to use stress-strength analysis to estimate the reliability of a component used in a vehicle. The stress is the usage mileage distribution and the strength is the failure mileage distribution of the component. The warranty is 1 year or 15,000 miles, whichever is earlier. The table below gives the mileage distribution per year.  


{| border="1" class="wikitable" style="margin: 1em auto 1em auto"
{| cellspacing="0" border="1" style="margin: 1em auto;" class="wikitable"
| align="center" style="background:#f0f0f0;"|'''Stress: Mileage Distribution'''
| align="center" style="background:#f0f0f0;"|''''''
|-
|-
| 10096||12405
| align="center" style="background: none repeat scroll 0% 0% rgb(240, 240, 240);" colspan="2" | '''Stress:&nbsp;Usage Mileage Distribution'''<br>
|-
|-
| 10469||12527
| align="center" | 10096
| align="center" | 12405
|-
|-
| 10955||12536
| align="center" | 10469
| align="center" | 12527
|-
|-
| 11183||12595
| align="center" | 10955
| align="center" | 12536
|-
|-
| 11391||12657
| align="center" | 11183
| align="center" | 12595
|-
|-
| 11486||13777
| align="center" | 11391
| align="center" | 12657
|-
|-
| 11534||13862
| align="center" | 11486
| align="center" | 13777
|-
|-
| 11919||13971
| align="center" | 11534
| align="center" | 13862
|-
|-
| 12105||14032
| align="center" | 11919
| align="center" | 13971
|-
|-
| 12141||14138
| align="center" | 12105
| align="center" | 14032
|-
|-
|  
| align="center" | 12141
| align="center" | 14138
|}
|}


<br> The next table gives the strength distribution or the failure mileage distribution.


The next table gives the strength distribution or the failure mileage distribution.
{| cellspacing="0" border="1" style="margin: 1em auto;" class="wikitable"
 
{|border="1" class="wikitable" style="margin: 1em auto 1em auto"
| align="center" style="background:#f0f0f0;"|'''Strength: Failure Distribution'''
| align="center" style="background:#f0f0f0;"|''''''
|-
|-
| 13507||16125
| align="center" style="background: none repeat scroll 0% 0% rgb(240, 240, 240);" colspan="2" | '''Strength: Failure Mileage Distribution'''<br>
|-
|-
| 13793||16320
| align="center" | 13507
| align="center" | 16125
|-
|-
| 13943||16327
| align="center" | 13793
| align="center" | 16320
|-
|-
| 14017||16349
| align="center" | 13943
| align="center" | 16327
|-
|-
| 14147||16406
| align="center" | 14017
| align="center" | 16349
|-
|-
| 14351||16501
| align="center" | 14147
| align="center" | 16406
|-
|-
| 14376||16611
| align="center" | 14351
| align="center" | 16501
|-
|-
| 14595||16625
| align="center" | 14376
| align="center" | 16611
|-
|-
| 14746||16670
| align="center" | 14595
| align="center" | 16625
|-
|-
| 14810||16749
| align="center" | 14746
| align="center" | 16670
|-
|-
| 14940||16793
| align="center" | 14810
| align="center" | 16749
|-
|-
| 14951||16862
| align="center" | 14940
| align="center" | 16793
|-
|-
| 15104||16930
| align="center" | 14951
| align="center" | 16862
|-
|-
| 15218||16948
| align="center" | 15104
| align="center" | 16930
|-
|-
| 15303||17024
| align="center" | 15218
| align="center" | 16948
|-
|-
| 15311||17041
| align="center" | 15303
| align="center" | 17024
|-
|-
| 15480||17263
| align="center" | 15311
| align="center" | 17041
|-
|-
| 15496||17347
| align="center" | 15480
| align="center" | 17263
|-
|-
| 15522||17430
| align="center" | 15496
| align="center" | 17347
|-
|-
| 15547||17805
| align="center" | 15522
| align="center" | 17430
|-
|-
| 15570||17884
| align="center" | 15547
| align="center" | 17805
|-
|-
| 15975||18549
| align="center" | 15570
| align="center" | 17884
|-
|-
| 16003||18575
| align="center" | 15975
| align="center" | 18549
|-
|-
| 16018||18813
| align="center" | 16003
| align="center" | 18575
|-
|-
| 16052||18944
| align="center" | 16018
| align="center" | 18813
|-
|-
|  
| align="center" | 16052
| align="center" | 18944
|}
|}


The goal is to estimate the reliability of the component within the warranty period (1 year/15,000 miles).
The goal is to estimate the reliability of the component within the warranty period (1 year/15,000 miles).  
 


'''Solution'''
<br> '''Solution'''  


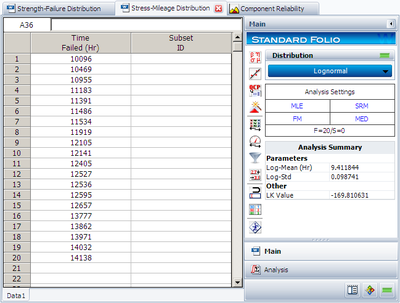
First, we need to estimate the stress and strength distributions using the above data. The estimated stress distribution is:
First, we need to estimate the stress and strength distributions using the above data. The estimated stress distribution is:  


[[Image: Stress-Strength Example 1 Stress-Distribution.png|thumb|center|400px]]
[[Image:Stress-Strength Example 1 Stress-Distribution.png|thumb|center|400px]]  


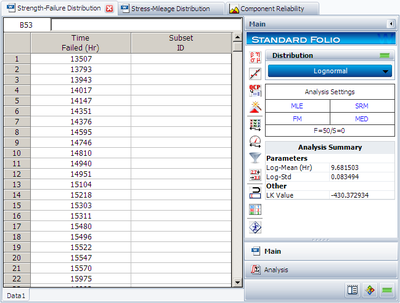
The estimated strength distribution is:
The estimated strength distribution is:  


[[Image: Stress-Strength Example 1 Strength-Distribution.png|thumb|center|400px]]
[[Image:Stress-Strength Example 1 Strength-Distribution.png|thumb|center|400px]]  


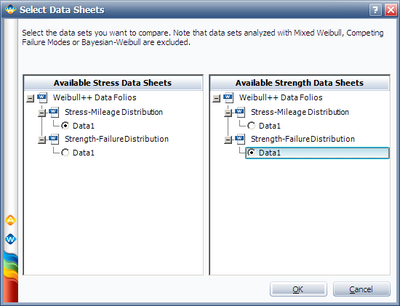
Add one '''Stress-Strength''' folio and choose the stress and strength distributions:
Add one '''Stress-Strength''' folio and choose the stress and strength distributions:  


[[Image: Stress-Strength Example 1 Choose Folios.png|thumb|center|400px]]
[[Image:Stress-Strength Example 1 Choose Folios.png|thumb|center|400px]]  


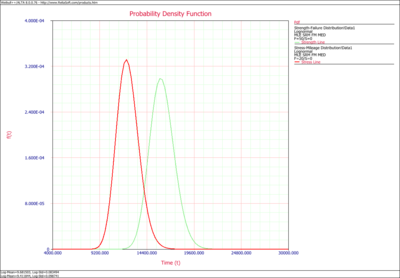
The stress-strength tool shows the ''pdf'' of the selected data folio. The ''pdf'' curves are shown next:
The stress-strength tool shows the ''pdfs'' of the selected data folios. The ''pdf'' curves are shown next:  


[[Image: Stress-Strength Example 1 pdf curve.png|thumb|center|400px]]
[[Image:Stress-Strength Example 1 pdf curve.png|thumb|center|400px]]  


Since the warranty is 1 year/15,000 miles, all the vehicles with mileage larger than 15,000 should not be considered in the calculation. Therefore, the conditional stress distribution conditioning on the mileage less than 15,000 should be used. This is done by using the following settings in the stress-strength calculation:
Since the warranty is 1 year/15,000 miles, all the vehicles with mileage larger than 15,000 should not be considered in the calculation. Therefore, the conditional stress distribution conditioning on the mileage less than 15,000 should be used. This is done by using the following settings in the tool:  


[[Image: Stress-Strength Example 1 Calculation Settings.png|thumb|center|400px]]
[[Image:Stress-Strength Example 1 Calculation Settings.png|thumb|center|400px]]  


The calculated results are given in below:
The calculated results are:  


[[Image: Stress-Strength Example 1 Calculation Results.png|thumb|center|400px]]
[[Image:Stress-Strength Example 1 Calculation Results.png|thumb|center|400px]]  


The estimated reliability for vehicles less than 15,000 miles per year is 98.84%. The associated confidence bounds are estimated from the variance of the distribution parameters. With larger samples for the stress and strength data, the width of the bounds will be narrower.
The estimated reliability for vehicles less than 15,000 miles per year is 98.84%. The associated confidence bounds are estimated from the variance of the distribution parameters. With larger samples for the stress and strength data, the width of the bounds will be narrower.

Revision as of 01:41, 30 March 2012

Stress-Strength Analysis with Parameter Uncertainty

Assume we are going to use stress-strength analysis to estimate the reliability of a component used in a vehicle. The stress is the usage mileage distribution and the strength is the failure mileage distribution of the component. The warranty is 1 year or 15,000 miles, whichever is earlier. The table below gives the mileage distribution per year.

Stress: Usage Mileage Distribution
10096 12405
10469 12527
10955 12536
11183 12595
11391 12657
11486 13777
11534 13862
11919 13971
12105 14032
12141 14138


The next table gives the strength distribution or the failure mileage distribution.

Strength: Failure Mileage Distribution
13507 16125
13793 16320
13943 16327
14017 16349
14147 16406
14351 16501
14376 16611
14595 16625
14746 16670
14810 16749
14940 16793
14951 16862
15104 16930
15218 16948
15303 17024
15311 17041
15480 17263
15496 17347
15522 17430
15547 17805
15570 17884
15975 18549
16003 18575
16018 18813
16052 18944

The goal is to estimate the reliability of the component within the warranty period (1 year/15,000 miles).


Solution

First, we need to estimate the stress and strength distributions using the above data. The estimated stress distribution is:

Stress-Strength Example 1 Stress-Distribution.png

The estimated strength distribution is:

Stress-Strength Example 1 Strength-Distribution.png

Add one Stress-Strength folio and choose the stress and strength distributions:

Stress-Strength Example 1 Choose Folios.png

The stress-strength tool shows the pdfs of the selected data folios. The pdf curves are shown next:

Stress-Strength Example 1 pdf curve.png

Since the warranty is 1 year/15,000 miles, all the vehicles with mileage larger than 15,000 should not be considered in the calculation. Therefore, the conditional stress distribution conditioning on the mileage less than 15,000 should be used. This is done by using the following settings in the tool:

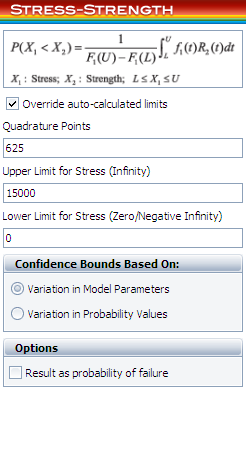
Stress-Strength Example 1 Calculation Settings.png

The calculated results are:

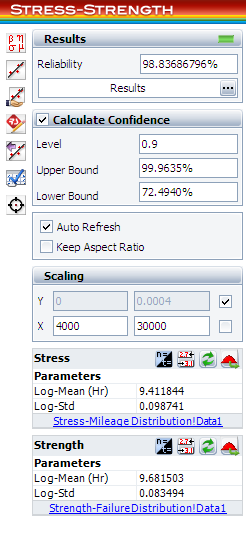
Stress-Strength Example 1 Calculation Results.png

The estimated reliability for vehicles less than 15,000 miles per year is 98.84%. The associated confidence bounds are estimated from the variance of the distribution parameters. With larger samples for the stress and strength data, the width of the bounds will be narrower.

Retrieved from "https://www.reliawiki.com/index.php?title=Template:Example:_Stress-Strength_Analysis_with_Parameter_Uncertainty&oldid=22982"