Arrhenius Relationship: Difference between revisions
Chuck Smith (talk | contribs) |
|||
| Line 15: | Line 15: | ||
<br> | <br> | ||
[[Image:ALTA6.2.png|center| | [[Image:ALTA6.2.png|center|200px|Arrhenius plot for Weibull life distribution.]] | ||
<br> | <br> | ||
| Line 23: | Line 23: | ||
::<math></math> | ::<math></math> | ||
<br> | <br> | ||
[[Image:ALTA6.3.png|center| | [[Image:ALTA6.3.png|center|200px|An illustration of both reciprocal and non-reciprocal scales.]] | ||
<br> | <br> | ||
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life. | The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life. | ||
| Line 30: | Line 30: | ||
::<math></math> | ::<math></math> | ||
<br> | <br> | ||
[[Image:ALTA6.4.png|center| | [[Image:ALTA6.4.png|center|200px|An example of scatter in life at each test stress level.]] | ||
<br> | <br> | ||
| Line 46: | Line 46: | ||
::<math></math> | ::<math></math> | ||
[[Image:ALTA6.5.png|center| | [[Image:ALTA6.5.png|center|200px|Behavior of the parameter ''B''.]] | ||
<br> | <br> | ||
Revision as of 15:57, 26 April 2012
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887.
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887. Template loop detected: Template:Arrhenius formulation
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
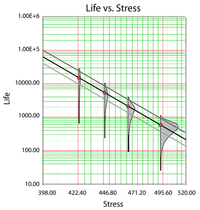
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
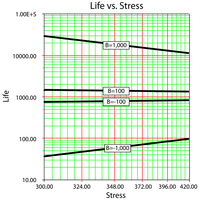
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Template loop detected: Template:A-a acceleration
Template loop detected: Template:Aae
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
- Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
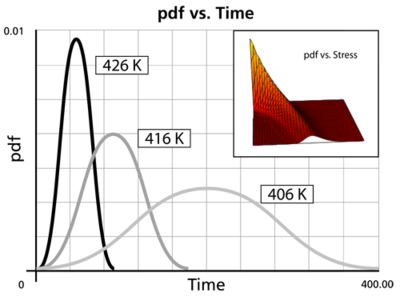
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
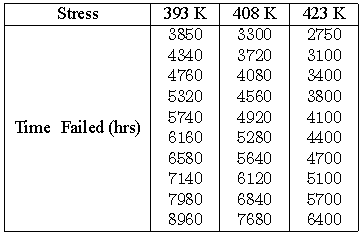
Consider the following times-to-failure data at three different stress levels.
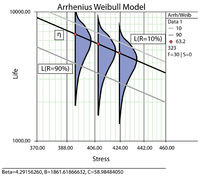
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
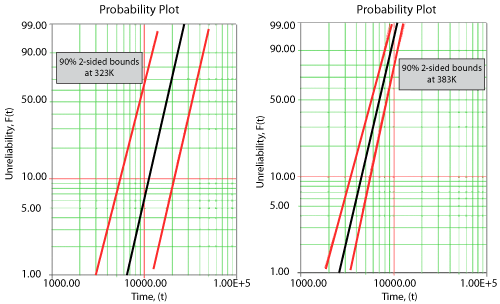
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887. Template loop detected: Template:Arrhenius formulation
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Template loop detected: Template:A-a acceleration
Template loop detected: Template:Aae
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
- Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887. Template loop detected: Template:Arrhenius formulation
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Template loop detected: Template:A-a acceleration
Template loop detected: Template:Aae
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
- Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/accelerated_life_testing_data_analysis
|
Chapter 4: Arrhenius Relationship |
Available Software: More Resources: |
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887. Template loop detected: Template:Arrhenius formulation
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Template loop detected: Template:A-a acceleration
Template loop detected: Template:Aae
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
- Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887. Template loop detected: Template:Arrhenius formulation
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Template loop detected: Template:A-a acceleration
Template loop detected: Template:Aae
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
- Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
Parameter Estimation
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887. Template loop detected: Template:Arrhenius formulation
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Template loop detected: Template:A-a acceleration
Template loop detected: Template:Aae
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
- Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887. Template loop detected: Template:Arrhenius formulation
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Template loop detected: Template:A-a acceleration
Template loop detected: Template:Aae
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
- Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887. Template loop detected: Template:Arrhenius formulation
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Template loop detected: Template:A-a acceleration
Template loop detected: Template:Aae
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
- Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds