Electronic Components Example

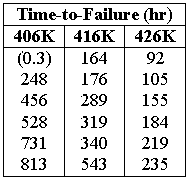
An electronic component was redesigned and was tested to failure at three different temperatures. Six units were tested at each stress level. At the 406K stress level however, a unit was removed from the test due to a test equipment failure which led to a failure of the component. A warranty time of one year is to be given, with an expected return of 10% of the population. The times-to-failure and test temperatures are given next:

The operating temperature is 356K. Using the Arrhenius-Weibull model, determine the following:

1) Should the first failure at 406K be included in the analysis?

2) Determine the warranty time for a 90% reliability.

3) Determine the 90% lower confidence limit on the warranty time.

4) Is the warranty requirement met? If not, what steps should be taken?

5) Repeat the analysis with the unrelated failure included. Is there any difference?

6) If the unrelated failure occurred at 500 hr, should it be included in the analysis?

Solution

1) Since the failure occurred at the very beginning of the test and for an unrelated reason, it can be omitted from the analysis. If it is included it should be treated as a suspension and not as a failure.

2) The first failure at 406K was neglected and the data were analyzed using ALTA. The following parameters were obtained:

[math]\displaystyle{ \begin{align} \beta =\ & 2.965820 \\ B=\ & 10679.567542 \\ C=\ & 2.396615\cdot {{10}^{-9}} \end{align} }[/math]

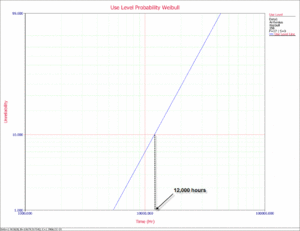
The use level probability plot (at 356K) can then be obtained. The warranty time for a reliability of 90% (or an unreliability of 10%) can be estimated from this plot as shown next.

The probability plot at use stress level.

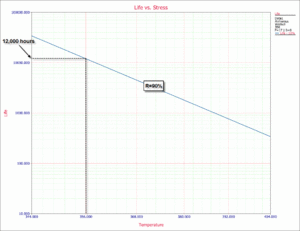
This estimate can also be obtained from the Arrhenius plot (a Life vs. Stress plot). The 10th percentile (time for a reliability of 90%) is plotted versus stress. This type of plot is useful because a time for a given reliability can be determined for different stress levels.

10% unreliability vs stress.

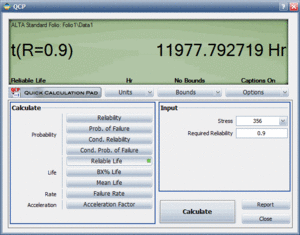
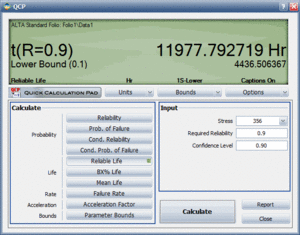
A more accurate way to determine the warranty time would be to use ALTA's Quick Calculation Pad (QCP). By selecting the Reliable Life option from in the QCP and entering 356 for the temperature and 0.9 for the required reliability, a reliable life of 11,977.792719 hr can be determined, as shown next:

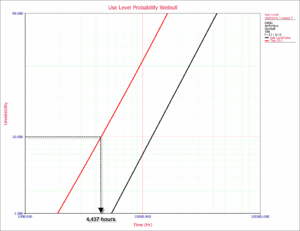
3) The warranty time for a 90% reliability was estimated to be approximately 12,000 hr. This is above the 1 year (8,760 hr) requirement. However, this is an estimate at the 50% confidence level. In other words, 50% of the time life will be greater than 12,000 hr and 50% of the time life will be less. A known confidence level is therefore crucial before any decisions are made. Using ALTA, confidence bounds can be plotted on both probability and Arrhenius plots. In the following use level probability plot, the 90% lower confidence level (LCL) is plotted. Note that percentile bounds are Type 1 confidence bounds in ALTA.

The use level probability plot with the Type I 90% lower bound.

An estimated 4,437 hr warranty time at a 90% lower confidence level was obtained from the use level probability plot. This means that 90% of the time, life will be greater than this value. In other words, a life of 4,437 hr is a bounding value for the warranty.

The Arrhenius plot with the 90% lower confidence level is shown next.

Life vs Stress plot with the 90% lower confidence level.

Using the QCP and specifying a 90% lower confidence level, a warranty time of 4436.5 hr is estimated, as shown next.

4) The warranty time for this component is estimated to be 4,436.5 hr at a 90% lower confidence bound. This is much less than the 1 year warranty time required (almost 6 months). Thus the desired warranty is not met. In this case, the following four options are available:

a) Redesign.

b) Reduce the confidence level.

c) Change the warranty policy.

d) Test additional units at stress levels closer to the use level.

5) Including the unrelated failure of 0.3 hr at 406 K (by treating it as a suspension at that time), the following results are obtained:

[math]\displaystyle{ \begin{align} \beta =\ & 2.965804 \\ B=\ & 10679.566625 \\ C=\ & 2.396619\cdot {{10}^{-9}} \end{align} }[/math]

These results are essentially identical to the ones with the unrelated failure excluded. A small difference can be seen only if more significant digits are considered. The warranty time with the 90% lower 1-sided confidence bound was estimated to be:

[math]\displaystyle{ \begin{align} T=\ & 11977.729145\text{ hr} \\ {{T}_{L}}=\ & 4436.462084\text{ hr} \end{align} }[/math]

Again, the difference is negligible. This is due to the very early time at which this unrelated failure occurred.

6) The analysis is repeated treating the unrelated failure at 500 hr as a suspension, with the following results:

[math]\displaystyle{ \begin{align} \beta =\ & 3.022714 \\ B=\ & 10959.523204 \\ C=\ & 1.23808\cdot {{10}^{-9}} \end{align} }[/math]

In this case, the results are very different. The warranty time with the 90% lower 1-sided confidence bound is estimated to be:

[math]\displaystyle{ \begin{align} T=\ & 13780.208409\text{ hr} \\ {{T}_{L}}=\ & 5303.672050\text{ hr} \end{align} }[/math]

It can be seen that in this case, it would be a mistake to neglect the unrelated failure. By neglecting this failure, we would actually underestimate the warranty time. The important observation in this example is that every piece of life information is crucial. In other words, unrelated failures also provide information about the life of the product. An unrelated failure occurring at 500 hr indicates that the product has survived for that period of time under the particular stress level, thus neglecting it would be a mistake. On the other hand it would also be a mistake to treat this data point as a failure, since the failure was caused by a test equipment failure.