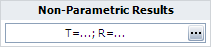Template:Weibull++ Non-Parametric LDA Plot Example: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
'''Weibull++ Non-Parametric LDA Plot Example''' | '''Weibull++ Non-Parametric LDA Plot Example''' | ||
This example shows how to use Weibull++ to do non-parametric LDA analysis. Weibull++ has three different non-parametric LDA method: Kaplan-Meier, Actuarial Standard, and Actuarial Simple. They are very similar. | This example shows how to use Weibull++ to do non-parametric LDA analysis. Weibull++ has three different non-parametric LDA method: '''Kaplan-Meier''', '''Actuarial Standard''', and '''Actuarial Simple'''. They are very similar. | ||
Assume we have the following data. | Assume we have the following data. | ||
Revision as of 17:52, 7 March 2012
Weibull++ Non-Parametric LDA Plot Example
This example shows how to use Weibull++ to do non-parametric LDA analysis. Weibull++ has three different non-parametric LDA method: Kaplan-Meier, Actuarial Standard, and Actuarial Simple. They are very similar.
Assume we have the following data.
| Number in State | State F or S | State End Time |
| 3 | F | 9 |
| 1 | S | 9 |
| 1 | F | 11 |
| 1 | S | 12 |
| 1 | F | 13 |
| 1 | S | 13 |
| 1 | S | 15 |
| 1 | F | 17 |
| 1 | F | 21 |
| 1 | S | 22 |
| 1 | S | 24 |
| 1 | S | 26 |
| 1 | F | 28 |
| 1 | F | 30 |
| 1 | S | 32 |
| 2 | S | 35 |
| 1 | S | 39 |
| 1 | S | 41 |
Please analyze the above data using Kaplan-Meier method in Weibull++.
Solution
Step 1: Create a Non-Parametric Specialized Folio.
Step 2: Enter the data as given in below Figure:
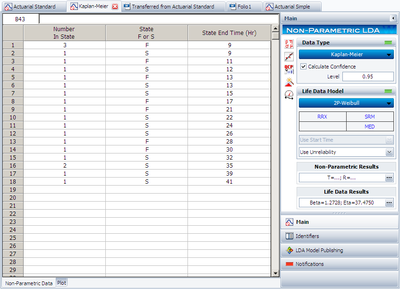
In the control panel, a confidence level can be entered. Reliability at each State End Time is calculated and plotted together with the confidence bounds.
Step 3: Plot the result.
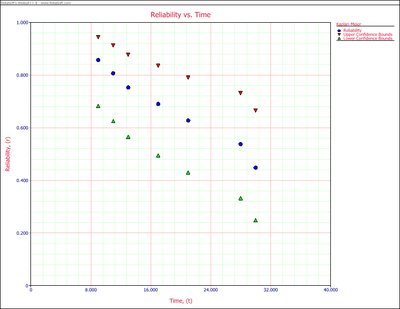
Since the analysis is done by non-parametric method, only the reliability at the observed state time can be calculated. Non-parametric methods cannot be used for extrapolation and interpolation.
Step 4: The results also can be viewed by clicking Non-Parametric Results: