Template:Aw characteristics: Difference between revisions
Chris Kahn (talk | contribs) |
Chris Kahn (talk | contribs) |
||
| Line 2: | Line 2: | ||
The characteristics of the 2-parameter Weibull distribution can be exemplified by examining the two parameters, beta, <math>\beta ,</math> and eta, <math>\eta ,</math> and the effect they have on the <math>pdf,</math> reliability and failure rate functions. | The characteristics of the 2-parameter Weibull distribution can be exemplified by examining the two parameters, beta, <math>\beta ,</math> and eta, <math>\eta ,</math> and the effect they have on the <math>pdf,</math> reliability and failure rate functions. | ||
====Looking at | ==== Looking at <span class="texhtml">β</span> ==== | ||
Beta | |||
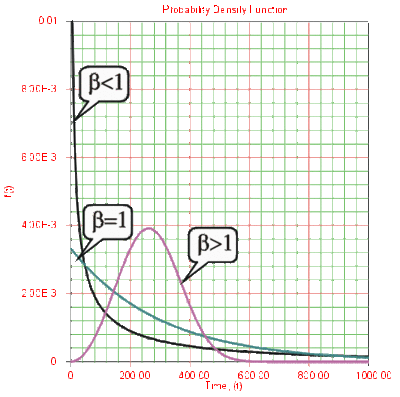
<br> | Beta (<span class="texhtml">β</span>) is called the shape parameter or slope of the Weibull distribution. Changing the value of <span class="texhtml">β</span> forces a change in the shape of the <span class="texhtml">''p''''d''''f''</span> as shown in the next figure. In addition, when the <span class="texhtml">''c''''d''''f''</span> is plotted on Weibull probability paper, a change in beta is a change in the slope of the distribution on Weibull probability paper. <br> '''Effects of <span class="texhtml">β</span> on the ''pdf''''' | ||
'''Effects of | |||
<br> | <br> [[Image:ALTA4.3.gif|thumb|center|400px]] <br> | ||
[[Image:ALTA4.3.gif|thumb|center|400px | |||
<br> | :*For <span class="texhtml">0 < β < 1</span> , the failure rate decreases with time and: | ||
::*As <math>T\to 0,</math> <math>f(T)\to \infty .</math> | |||
:* For | ::*As <math>T\to \infty </math> , <math>f(T)\to 0</math> . | ||
::* As | ::*<span class="texhtml">''f''(''T'')</span> decreases monotonically and is convex as <span class="texhtml">''T''</span> increases. | ||
::* As | ::*The mode is non-existent. | ||
::* | :*For <span class="texhtml">β = 1,</span> it becomes the exponential distribution, as a special case, <br> | ||
::* The mode is non-existent. | |||
:* For | <br> | ||
<br> | |||
:or: | :or: | ||
<br> | |||
<br> | |||
::<math>f(T)=\frac{1}{\eta }{{e}^{-\tfrac{T}{\eta }}};\text{ }\eta >0,T\ge 0</math> | ::<math>f(T)=\frac{1}{\eta }{{e}^{-\tfrac{T}{\eta }}};\text{ }\eta >0,T\ge 0</math> | ||
<br> | <br> | ||
''' | |||
<br> | :where <math>\tfrac{1}{\eta }=\lambda =</math> chance, useful life, or failure rate. | ||
[[Image:ALTA4.4.gif|thumb|center|400px| | |||
<br> | |||
:*For <span class="texhtml">β > 1</span> , <span class="texhtml">''f''(''T''),</span> the Weibull assumes wear-out type shapes (i.e. the failure rate increases with time) and: | |||
::*<span class="texhtml">''f''(''T'') = 0</span> at <span class="texhtml">''T'' = 0</span> . | |||
::*<span class="texhtml">''f''(''T'')</span> increases as <math>T\to \tilde{T}</math> (mode) and decreases thereafter. | |||
::*For <span class="texhtml">β = 2</span> it becomes the Rayleigh distribution as a special case. For <span class="texhtml">β < 2.6</span> the Weibull <span class="texhtml">''p''''d''''f''</span> is positively skewed (has a right tail), for <span class="texhtml">2.6 < β < 3.7</span> its coefficient of skewness approaches zero (no tail); consequently, it may approximate the normal <span class="texhtml">''p''''d''''f''</span> , and for <span class="texhtml">β > 3.7</span> it is negatively skewed (left tail). | |||
:*The parameter <span class="texhtml">β</span> is a pure number, i.e. it is dimensionless. | |||
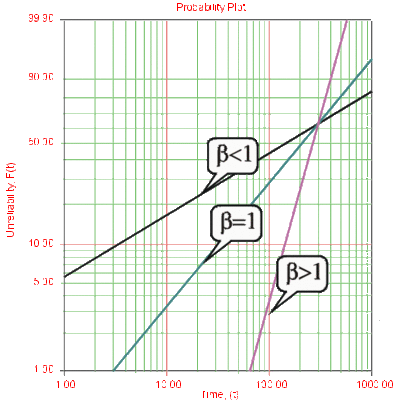
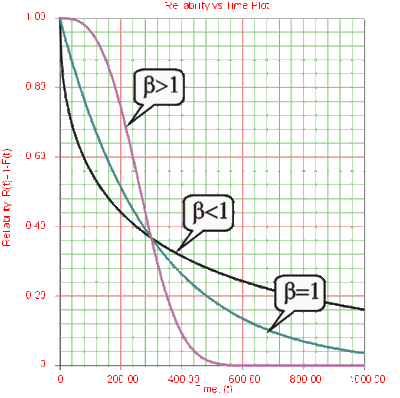
<br> '''Effects of <span class="texhtml">β</span> on the Reliability Function and the ''cdf''''' | |||
<br> [[Image:ALTA4.4.gif|thumb|center|400px]] | |||
<br> [[Image:ALTA4.5.gif|thumb|center|400px]] | |||
<br> | |||
:*<span class="texhtml">''R''(''T'')</span> decreases sharply and monotonically for <span class="texhtml">0 < β < 1</span> , it is convex, and decreases less sharply for the same <span class="texhtml">β</span> . | |||
:*For <span class="texhtml">β = 1</span> and the same <span class="texhtml">η</span> , <span class="texhtml">''R''(''T'')</span> decreases monotonically but less sharply than for <span class="texhtml">0 < β < 1</span> , and is convex. | |||
:*For <span class="texhtml">β > 1</span> , <span class="texhtml">''R''(''T'')</span> decreases as <span class="texhtml">''T''</span> increases but less sharply than before, and as wear-out sets in, it decreases sharply and goes through an inflection point. | |||
<br> | |||
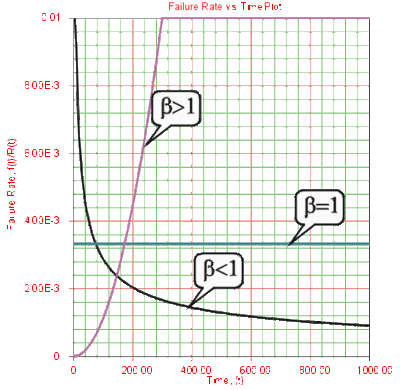
'''Effects of <span class="texhtml">β</span> on the Failure Rate Function''' | |||
[[Image:ALTA4.6.gif|thumb|center|400px]] <br> | |||
:*The Weibull failure rate for <span class="texhtml">0 < β < 1</span> is unbounded at <span class="texhtml">''T'' = 0</span> . The failure rate, <span class="texhtml">λ(''T''),</span> decreases thereafter monotonically and is convex, approaching the value of zero as <math>T\to \infty </math> or <math>\lambda (\infty )=0</math> . This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When such behavior is encountered, one or more of the following conclusions can be drawn: | |||
::*Burn-in testing and/or environmental stress screening are not well implemented. | |||
::*There are problems in the production line. | |||
::*Inadequate quality control. | |||
::*Packaging and transit problems. | |||
:*For <span class="texhtml">β = 1</span> , <span class="texhtml">λ(''T'')</span> yields a constant value of <math>\tfrac{1}{\eta }</math> , or: | |||
::<math>\lambda (T)=\lambda =\frac{1}{\eta }</math> | |||
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units. | |||
:*For <span class="texhtml">β > 1</span> , <span class="texhtml">λ(''T'')</span> increases as <span class="texhtml">''T''</span> increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For <span class="texhtml">1 < β < 2</span> the <span class="texhtml">λ(''T'')</span> curve is concave, consequently the failure rate increases at a decreasing rate as <span class="texhtml">''T''</span> increases. | |||
:*For <span class="texhtml">β = 2</span> , or for the Rayleigh distribution case, the failure rate function is given by: | |||
::<math>\lambda (T)=\frac{2}{\eta }\left( \frac{T}{\eta } \right)</math> | |||
<br> | <br> Hence there emerges a straight line relationship between <span class="texhtml">λ(''T'')</span> and <span class="texhtml">''T''</span> , starting at a value of <span class="texhtml">λ(''T'') = 0</span> at <span class="texhtml">''T'' = 0</span> and increasing thereafter with a slope of <math>\tfrac{2}{{{\eta }^{2}}}</math> . Consequently, the failure rate increases at a constant rate as <span class="texhtml">''T''</span> increases. Furthermore, if <span class="texhtml">η = 1</span> the slope becomes equal to 2, and <span class="texhtml">λ(''T'')</span> becomes a straight line which passes through the origin with a slope of 2. | ||
:*When <span class="texhtml">β > 2</span> the <span class="texhtml">λ(''T'')</span> curve is convex, with its slope increasing as <span class="texhtml">''T''</span> increases. Consequently, the failure rate increases at an increasing rate as <span class="texhtml">''T''</span> increases, indicating wear-out life. | |||
:* | |||
<br> | <br> | ||
Revision as of 23:36, 6 March 2012
Characteristics
The characteristics of the 2-parameter Weibull distribution can be exemplified by examining the two parameters, beta, [math]\displaystyle{ \beta , }[/math] and eta, [math]\displaystyle{ \eta , }[/math] and the effect they have on the [math]\displaystyle{ pdf, }[/math] reliability and failure rate functions.
Looking at β
Beta (β) is called the shape parameter or slope of the Weibull distribution. Changing the value of β forces a change in the shape of the p'd'f as shown in the next figure. In addition, when the c'd'f is plotted on Weibull probability paper, a change in beta is a change in the slope of the distribution on Weibull probability paper.
Effects of β on the pdf
- For 0 < β < 1 , the failure rate decreases with time and:
- As [math]\displaystyle{ T\to 0, }[/math] [math]\displaystyle{ f(T)\to \infty . }[/math]
- As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ f(T)\to 0 }[/math] .
- f(T) decreases monotonically and is convex as T increases.
- The mode is non-existent.
- For β = 1, it becomes the exponential distribution, as a special case,
- or:
- [math]\displaystyle{ f(T)=\frac{1}{\eta }{{e}^{-\tfrac{T}{\eta }}};\text{ }\eta \gt 0,T\ge 0 }[/math]
- where [math]\displaystyle{ \tfrac{1}{\eta }=\lambda = }[/math] chance, useful life, or failure rate.
- For β > 1 , f(T), the Weibull assumes wear-out type shapes (i.e. the failure rate increases with time) and:
- f(T) = 0 at T = 0 .
- f(T) increases as [math]\displaystyle{ T\to \tilde{T} }[/math] (mode) and decreases thereafter.
- For β = 2 it becomes the Rayleigh distribution as a special case. For β < 2.6 the Weibull p'd'f is positively skewed (has a right tail), for 2.6 < β < 3.7 its coefficient of skewness approaches zero (no tail); consequently, it may approximate the normal p'd'f , and for β > 3.7 it is negatively skewed (left tail).
- The parameter β is a pure number, i.e. it is dimensionless.
Effects of β on the Reliability Function and the cdf
- R(T) decreases sharply and monotonically for 0 < β < 1 , it is convex, and decreases less sharply for the same β .
- For β = 1 and the same η , R(T) decreases monotonically but less sharply than for 0 < β < 1 , and is convex.
- For β > 1 , R(T) decreases as T increases but less sharply than before, and as wear-out sets in, it decreases sharply and goes through an inflection point.
Effects of β on the Failure Rate Function
- The Weibull failure rate for 0 < β < 1 is unbounded at T = 0 . The failure rate, λ(T), decreases thereafter monotonically and is convex, approaching the value of zero as [math]\displaystyle{ T\to \infty }[/math] or [math]\displaystyle{ \lambda (\infty )=0 }[/math] . This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When such behavior is encountered, one or more of the following conclusions can be drawn:
- Burn-in testing and/or environmental stress screening are not well implemented.
- There are problems in the production line.
- Inadequate quality control.
- Packaging and transit problems.
- For β = 1 , λ(T) yields a constant value of [math]\displaystyle{ \tfrac{1}{\eta } }[/math] , or:
- [math]\displaystyle{ \lambda (T)=\lambda =\frac{1}{\eta } }[/math]
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
- For β > 1 , λ(T) increases as T increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For 1 < β < 2 the λ(T) curve is concave, consequently the failure rate increases at a decreasing rate as T increases.
- For β = 2 , or for the Rayleigh distribution case, the failure rate function is given by:
- [math]\displaystyle{ \lambda (T)=\frac{2}{\eta }\left( \frac{T}{\eta } \right) }[/math]
Hence there emerges a straight line relationship between λ(T) and T , starting at a value of λ(T) = 0 at T = 0 and increasing thereafter with a slope of [math]\displaystyle{ \tfrac{2}{{{\eta }^{2}}} }[/math] . Consequently, the failure rate increases at a constant rate as T increases. Furthermore, if η = 1 the slope becomes equal to 2, and λ(T) becomes a straight line which passes through the origin with a slope of 2.
- When β > 2 the λ(T) curve is convex, with its slope increasing as T increases. Consequently, the failure rate increases at an increasing rate as T increases, indicating wear-out life.
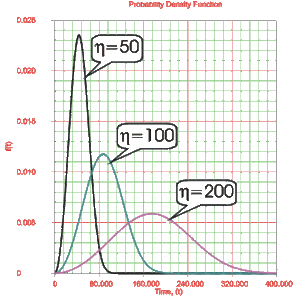
Looking at [math]\displaystyle{ \eta }[/math]
Eta, [math]\displaystyle{ \eta , }[/math] is called the scale parameter of the Weibull distribution. The parameter [math]\displaystyle{ \eta }[/math] has the same units as [math]\displaystyle{ T }[/math] , such as hours, miles, cycles, actuations, etc.
- • A change in the scale parameter [math]\displaystyle{ \eta }[/math] has the same effect on the distribution as a change of the abscissa scale.
- o If [math]\displaystyle{ \eta }[/math] is increased while [math]\displaystyle{ \beta }[/math] is kept the same, the distribution gets stretched out to the right and its height decreases, while maintaining its shape and location.
- o If [math]\displaystyle{ \eta }[/math] is decreased while [math]\displaystyle{ \beta }[/math] is kept the same, the distribution gets pushed in toward the left (i.e. toward its beginning, or 0) and its height increases.