Template:Example: Weibull Distribution Complete Data Example: Difference between revisions
No edit summary |
No edit summary |
||
| Line 11: | Line 11: | ||
Enter the data in the appropriate columns. Note that there are four suspensions, as only six of the ten units were tested to failure (the next figure shows the data as entered). Use the three-parameter Weibull and MLE for the calculations. | Enter the data in the appropriate columns. Note that there are four suspensions, as only six of the ten units were tested to failure (the next figure shows the data as entered). Use the three-parameter Weibull and MLE for the calculations. | ||
[[Image: DataforExample_11.png.png|thumb|center| | [[Image: DataforExample_11.png.png|thumb|center|250px]] | ||
Plot the data. | Plot the data. | ||
[[Image: Plot for Example 11.png|thumb|center| | [[Image: Plot for Example 11.png|thumb|center|250px]] | ||
Note that the original data points, on the curved line, were adjusted by subtracting 30.92 hours to yield a straight line as shown above. | Note that the original data points, on the curved line, were adjusted by subtracting 30.92 hours to yield a straight line as shown above. | ||
Revision as of 18:29, 25 April 2012
Weibull Distribution Complete Data Example
Assume that ten identical units (N = 10) are being reliability tested at the same application and operation stress levels. Six of these units fail during this test after operating the following numbers of hours, [math]\displaystyle{ {T}_{j} }[/math]: 150, 105, 83, 123, 64 and 46. The test is stopped at the sixth failure. Find the parameters of the Weibull pdf that represents these data.
Solution
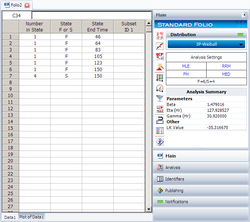
Open a new Data Folio choosing Times-to-failure data, My data set contains suspensions (right censored data) and I want to enter data in groups.
Enter the data in the appropriate columns. Note that there are four suspensions, as only six of the ten units were tested to failure (the next figure shows the data as entered). Use the three-parameter Weibull and MLE for the calculations.
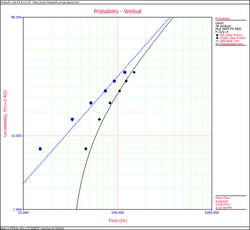
Plot the data.
Note that the original data points, on the curved line, were adjusted by subtracting 30.92 hours to yield a straight line as shown above.