Template:Alta prob plotting of ed: Difference between revisions
Chris Kahn (talk | contribs) No edit summary |
|||
| Line 1: | Line 1: | ||
====Probability Plotting==== | ==== Probability Plotting ==== | ||
<br> | One method of calculating the parameter of the exponential distribution is by using probability plotting. To better illustrate this procedure, consider the following example.<br> | ||
=====Example 1===== | ===== Example 1 ===== | ||
Let's assume six identical units are reliability tested at the same application and operation stress levels. All of these units fail during the test after operating for the following times (in hours), <span class="texhtml">''T''<sub>''i''</sub></span> : 96, 257, 498, 763, 1051 and 1744. <br> The steps for determining the parameters of the exponential ''pdf'' representing the data, using probability plotting, are as follows: <br> | |||
<br> | |||
:*Rank the times-to-failure in ascending order, as shown next. | |||
<br> | |||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
\text{Time-to-} & \text{Failure Order Number} \\ | \text{Time-to-} & \text{Failure Order Number} \\ | ||
\text{ | \text{Failure (Hr)} & \text{out of a Sample Size of 6} \\ | ||
\text{96} & \text{1} \\ | \text{96} & \text{1} \\ | ||
\text{257} & \text{2} \\ | \text{257} & \text{2} \\ | ||
| Line 24: | Line 19: | ||
\text{1,051} & \text{5} \\ | \text{1,051} & \text{5} \\ | ||
\text{1,744} & \text{6} \\ | \text{1,744} & \text{6} \\ | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
<br> | |||
:*Obtain their median rank plotting positions. | |||
<br> | |||
Median rank positions are used instead of other ranking methods because median ranks are at a specific confidence level (50%). | |||
:*The times-to-failure, with their corresponding median ranks, are shown next: | |||
: | |||
<br> | <br> | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
\text{Time-to-} & \text{Median} \\ | \text{Time-to-} & \text{Median} \\ | ||
\text{ | \text{Failure (Hr)} & \text{Rank, }% \\ | ||
\text{96} & \text{10}\text{.91} \\ | \text{96} & \text{10}\text{.91} \\ | ||
\text{257} & \text{26}\text{.44} \\ | \text{257} & \text{26}\text{.44} \\ | ||
| Line 43: | Line 40: | ||
\text{1,051} & \text{73}\text{.56} \\ | \text{1,051} & \text{73}\text{.56} \\ | ||
\text{1,744} & \text{89}\text{.10} \\ | \text{1,744} & \text{89}\text{.10} \\ | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
<br> | |||
:*On an exponential probability paper, plot the times on the x-axis and their corresponding rank value on the y-axis. The next figure displays an example of an exponential probability paper. The paper is simply a log-linear paper. | |||
<br> [[Image:ALTA4.1.gif|thumb|center|400px]] | |||
<br> | <br> | ||
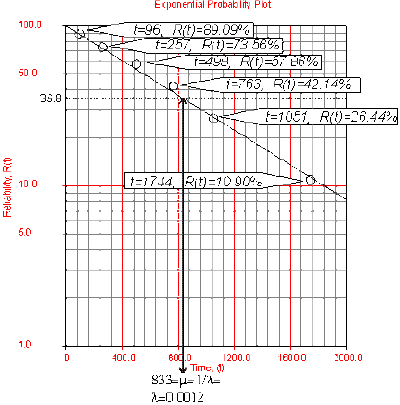
:*Draw the best possible straight line that goes through the <span class="texhtml">''t'' = 0</span> and <span class="texhtml">(''t'') = 100%</span> point and through the plotted points. | |||
:*At the <span class="texhtml">''Q''(''t'') = 63.2%</span> or <span class="texhtml">''R''(''t'') = 36.8%</span> ordinate point, draw a straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of the mean. For this case, <math>\widehat{\mu }=833</math> hr which means that <math>\lambda =\tfrac{1}{\mu }=0.0012</math> . (This is always at 63.2% since <math>(T)=1-{{e}^{-\tfrac{\mu }{\mu }}}=1-{{e}^{-1}}=0.632=63.2%</math>.) | |||
<br> [[Image:ALTA4.2.gif|thumb|center|400px]] <br> <br> Now any reliability value for any mission time <span class="texhtml">''t''</span> can be obtained. For example, the reliability for a mission of 15 hour (or any other time) can now be obtained either from the plot or analytically. | |||
<br> | |||
[[Image:ALTA4.2.gif|thumb|center|400px | |||
<br> | |||
<br> | |||
Now any reliability value for any mission time | |||
reliability for a mission of 15 | |||
To obtain the value from the plot, draw a vertical line from the abscissa, at <span class="texhtml">''t'' = 15</span> hr, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read <span class="texhtml">''R''(''t'')</span> . In this case, <span class="texhtml">''R''(''t'' = 15) = 98.15%</span> . This can also be obtained analytically, from the exponential reliability function. <br> | |||
To obtain the value from the plot, draw a vertical line from the abscissa, at | |||
hr, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read | |||
< | |||
analytically, from the exponential reliability function. | |||
<br> | |||
====MLE Parameter Estimation==== | ====MLE Parameter Estimation==== | ||
Revision as of 23:02, 6 March 2012
Probability Plotting
One method of calculating the parameter of the exponential distribution is by using probability plotting. To better illustrate this procedure, consider the following example.
Example 1
Let's assume six identical units are reliability tested at the same application and operation stress levels. All of these units fail during the test after operating for the following times (in hours), Ti : 96, 257, 498, 763, 1051 and 1744.
The steps for determining the parameters of the exponential pdf representing the data, using probability plotting, are as follows:
- Rank the times-to-failure in ascending order, as shown next.
- Obtain their median rank plotting positions.
Median rank positions are used instead of other ranking methods because median ranks are at a specific confidence level (50%).
- The times-to-failure, with their corresponding median ranks, are shown next:
- On an exponential probability paper, plot the times on the x-axis and their corresponding rank value on the y-axis. The next figure displays an example of an exponential probability paper. The paper is simply a log-linear paper.
- Draw the best possible straight line that goes through the t = 0 and (t) = 100% point and through the plotted points.
- At the Q(t) = 63.2% or R(t) = 36.8% ordinate point, draw a straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of the mean. For this case, [math]\displaystyle{ \widehat{\mu }=833 }[/math] hr which means that [math]\displaystyle{ \lambda =\tfrac{1}{\mu }=0.0012 }[/math] . (This is always at 63.2% since [math]\displaystyle{ (T)=1-{{e}^{-\tfrac{\mu }{\mu }}}=1-{{e}^{-1}}=0.632=63.2% }[/math].)
Now any reliability value for any mission time t can be obtained. For example, the reliability for a mission of 15 hour (or any other time) can now be obtained either from the plot or analytically.
To obtain the value from the plot, draw a vertical line from the abscissa, at t = 15 hr, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read R(t) . In this case, R(t = 15) = 98.15% . This can also be obtained analytically, from the exponential reliability function.
MLE Parameter Estimation
The parameter of the exponential distribution can also be estimated using the maximum likelihood estimation (MLE) method. This log-likelihood function is:
- [math]\displaystyle{ \ln (L)=\Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] }[/math]
- where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\lambda T_{Li}^{\prime \prime }}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\lambda T_{Ri}^{\prime \prime }}} }[/math]
- and:
- • [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of times-to-failure data points.
- • [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
- • [math]\displaystyle{ \lambda }[/math] is the failure rate parameter (unknown a priori, the only parameter to be found).
- • [math]\displaystyle{ {{T}_{i}} }[/math] is the time of the [math]\displaystyle{ {{i}^{th}} }[/math] group of time-to-failure data.
- • [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
- • [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
- • [math]\displaystyle{ T_{i}^{\prime } }[/math] is the time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
- • [math]\displaystyle{ FI }[/math] is the number of interval data groups.
- • [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the i [math]\displaystyle{ ^{th} }[/math] group of data intervals.
- • [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the i [math]\displaystyle{ ^{th} }[/math] interval.
- • [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the i [math]\displaystyle{ ^{th} }[/math] interval.
The solution will be found by solving for a parameter [math]\displaystyle{ \widehat{\lambda } }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \lambda }=0 }[/math] where:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{1}{\lambda }-{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }T_{i}^{\prime }-\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} }[/math]
Example 2
Using the same data as in the probability plotting example (Example 1), and assuming an exponential distribution, estimate the parameter using the MLE method.
Solution
In this example we have non-grouped data without suspensions. Therefore:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,\left[ \frac{1}{\lambda }-\left( {{T}_{i}} \right) \right]=\underset{i=1}{\overset{14}{\mathop \sum }}\,\left[ \frac{1}{\lambda }-\left( {{T}_{i}} \right) \right]=0 }[/math]
Substituting the values for [math]\displaystyle{ T }[/math] we get:
- [math]\displaystyle{ \begin{align} \frac{6}{\lambda }&= 4409,\text{ or:} \\ \lambda& = 0.00136\text{ failure/hr} \end{align} }[/math]