Template:Characteristics of the gumbel distribution: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
Line 2: Line 2:
Some of the specific characteristics of the Gumbel distribution are the following:
Some of the specific characteristics of the Gumbel distribution are the following:


:• The shape of the Gumbel distribution is skewed to the left. The Gumbel  <math>pdf</math>  has no shape parameter. This means that the Gumbel  <math>pdf</math>  has only one shape, which does not change.
:* The shape of the Gumbel distribution is skewed to the left. The Gumbel  <math>pdf</math>  has no shape parameter. This means that the Gumbel  <math>pdf</math>  has only one shape, which does not change.
:• The Gumbel  <math>pdf</math>  has location parameter  <math>\mu ,</math>  which is equal to the mode  <math>\tilde{T},</math>  but it differs from median and mean. This is because the Gumbel distribution is not symmetrical about its  <math>\mu </math> .
:* The Gumbel  <math>pdf</math>  has location parameter  <math>\mu ,</math>  which is equal to the mode  <math>\tilde{T},</math>  but it differs from median and mean. This is because the Gumbel distribution is not symmetrical about its  <math>\mu </math> .
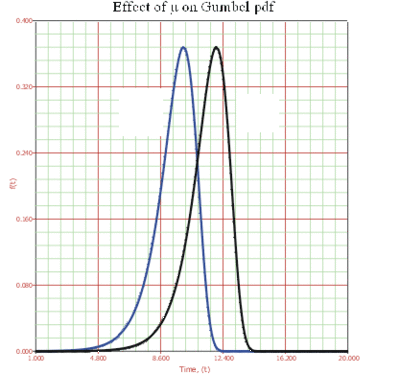
:• As  <math>\mu </math>  decreases, the  <math>pdf</math>  is shifted to the left.
:* As  <math>\mu </math>  decreases, the  <math>pdf</math>  is shifted to the left.
:• As  <math>\mu </math>  increases, the  <math>pdf</math>  is shifted to the right.
:* As  <math>\mu </math>  increases, the  <math>pdf</math>  is shifted to the right.


[[Image:effectofmuongumbel.gif|thumb|center|400px| ]]  
[[Image:effectofmuongumbel.gif|thumb|center|400px| ]]  


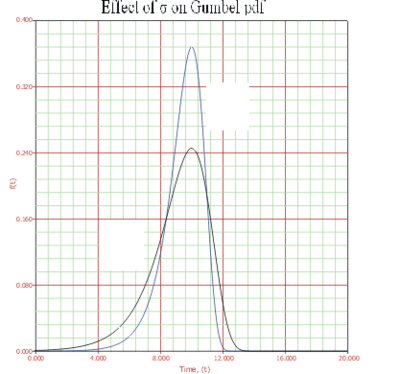
:• As  <math>\sigma </math>  increases, the  <math>pdf</math>  spreads out and becomes shallower.
:* As  <math>\sigma </math>  increases, the  <math>pdf</math>  spreads out and becomes shallower.
:• As  <math>\sigma </math>  decreases, the  <math>pdf</math>  becomes taller and narrower.
:* As  <math>\sigma </math>  decreases, the  <math>pdf</math>  becomes taller and narrower.
:• For  <math>T=\pm \infty ,</math>  <math>pdf=0.</math>  For  <math>T=\mu </math> , the  <math>pdf</math>  reaches its maximum point <math>\frac{1}{\sigma e}</math>
:* For  <math>T=\pm \infty ,</math>  <math>pdf=0.</math>  For  <math>T=\mu </math> , the  <math>pdf</math>  reaches its maximum point <math>\frac{1}{\sigma e}</math>


[[Image:effectofsigmaongumbel.gif|thumb|center|400px| ]]  
[[Image:effectofsigmaongumbel.gif|thumb|center|400px| ]]  


:• The points of inflection of the  <math>pdf</math>  graph are  <math>T=\mu \pm \sigma \ln (\tfrac{3\pm \sqrt{5}}{2})</math>  or  <math>T\approx \mu \pm \sigma 0.96242</math> .
:* The points of inflection of the  <math>pdf</math>  graph are  <math>T=\mu \pm \sigma \ln (\tfrac{3\pm \sqrt{5}}{2})</math>  or  <math>T\approx \mu \pm \sigma 0.96242</math> .
:• If times follow the Weibull distribution, then the logarithm of times follow a Gumbel distribution. If  <math>{{t}_{i}}</math>  follows a Weibull distribution with  <math>\beta </math>  and  <math>\eta </math>  , then the  <math>Ln({{t}_{i}})</math>  follows a Gumbel distribution with  <math>\mu =\ln (\eta )</math>  and  <math>\sigma =\tfrac{1}{\beta }</math>  [32] <math>.</math>
:* If times follow the Weibull distribution, then the logarithm of times follow a Gumbel distribution. If  <math>{{t}_{i}}</math>  follows a Weibull distribution with  <math>\beta </math>  and  <math>\eta </math>  , then the  <math>Ln({{t}_{i}})</math>  follows a Gumbel distribution with  <math>\mu =\ln (\eta )</math>  and  <math>\sigma =\tfrac{1}{\beta }</math>  [32] <math>.</math>

Revision as of 18:31, 20 February 2012

Characteristics of the Gumbel Distribution

Some of the specific characteristics of the Gumbel distribution are the following:

  • The shape of the Gumbel distribution is skewed to the left. The Gumbel [math]\displaystyle{ pdf }[/math] has no shape parameter. This means that the Gumbel [math]\displaystyle{ pdf }[/math] has only one shape, which does not change.
  • The Gumbel [math]\displaystyle{ pdf }[/math] has location parameter [math]\displaystyle{ \mu , }[/math] which is equal to the mode [math]\displaystyle{ \tilde{T}, }[/math] but it differs from median and mean. This is because the Gumbel distribution is not symmetrical about its [math]\displaystyle{ \mu }[/math] .
  • As [math]\displaystyle{ \mu }[/math] decreases, the [math]\displaystyle{ pdf }[/math] is shifted to the left.
  • As [math]\displaystyle{ \mu }[/math] increases, the [math]\displaystyle{ pdf }[/math] is shifted to the right.
Effectofmuongumbel.gif
  • As [math]\displaystyle{ \sigma }[/math] increases, the [math]\displaystyle{ pdf }[/math] spreads out and becomes shallower.
  • As [math]\displaystyle{ \sigma }[/math] decreases, the [math]\displaystyle{ pdf }[/math] becomes taller and narrower.
  • For [math]\displaystyle{ T=\pm \infty , }[/math] [math]\displaystyle{ pdf=0. }[/math] For [math]\displaystyle{ T=\mu }[/math] , the [math]\displaystyle{ pdf }[/math] reaches its maximum point [math]\displaystyle{ \frac{1}{\sigma e} }[/math]
Effectofsigmaongumbel.gif
  • The points of inflection of the [math]\displaystyle{ pdf }[/math] graph are [math]\displaystyle{ T=\mu \pm \sigma \ln (\tfrac{3\pm \sqrt{5}}{2}) }[/math] or [math]\displaystyle{ T\approx \mu \pm \sigma 0.96242 }[/math] .
  • If times follow the Weibull distribution, then the logarithm of times follow a Gumbel distribution. If [math]\displaystyle{ {{t}_{i}} }[/math] follows a Weibull distribution with [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \eta }[/math] , then the [math]\displaystyle{ Ln({{t}_{i}}) }[/math] follows a Gumbel distribution with [math]\displaystyle{ \mu =\ln (\eta ) }[/math] and [math]\displaystyle{ \sigma =\tfrac{1}{\beta } }[/math] [32] [math]\displaystyle{ . }[/math]
Retrieved from "https://www.reliawiki.com/index.php?title=Template:Characteristics_of_the_gumbel_distribution&oldid=16958"