Template:TNT Exponential: Difference between revisions
| Line 98: | Line 98: | ||
<br> | <br> | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{U_{i}^{n}}{C}{{e}^{-\tfrac{B}{{{V}_{i}}}}}\cdot {{e}^{-\tfrac{U_{i}^{n}}{C}\left( {{e}^{-\tfrac{B}{{{V}_{i}}}}} \right){{T}_{i}}}} \right] | & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{U_{i}^{n}}{C}{{e}^{-\tfrac{B}{{{V}_{i}}}}}\cdot {{e}^{-\tfrac{U_{i}^{n}}{C}\left( {{e}^{-\tfrac{B}{{{V}_{i}}}}} \right){{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{U_{i}^{n}}{C}\left( {{e}^{-\tfrac{B}{{{V}_{i}}}}} \right)T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] | ||
\end{align}</math> | \end{align}</math> | ||
<br> | <br> | ||
where: | |||
<br> | <br> | ||
| Line 112: | Line 111: | ||
<br> | <br> | ||
and: | |||
<br> | <br> | ||
• <math>{{F}_{e}}</math> is the number of groups of exact times-to-failure data points. | • <math>{{F}_{e}}</math> is the number of groups of exact times-to-failure data points. | ||
Revision as of 01:11, 17 February 2012
T-NT Exponential
By setting
T-NT Exponential Statistical Properties Summary
Mean or MTTF
The mean,
Median
The median,
Mode
The mode,
Standard Deviation
The standard deviation,
T-NT Exponential Reliability Function
The T-NT exponential reliability function is given by:
This function is the complement of the T-NT exponential cumulative distribution function or:
and,
Conditional Reliability
The conditional reliability function for the T-NT exponential model is given by,
Reliable Life
For the T-NT exponential model, the reliable life, or the mission duration for a desired reliability goal,
- or:
Parameter Estimation
Maximum Likelihood Estimation Method
Substituting the T-NT relationship into the exponential log-likelihood equation yields:
where:
and:
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
The solution (parameter estimates) will be found by solving for the parameters
When temperature and a second non-thermal stress (e.g., voltage) are the accelerated stresses of a test, then the Arrhenius and the inverse power law relationships can be combined to yield the Temperature-NonThermal (T-NT) relationship. This relationship is given by:
where:
The T-NT relationship can be linearized and plotted on a Life vs. Stress plot. The relationship is linearized by taking the natural logarithm of both sides in the T-NT relationship or:
Since life is now a function of two stresses, a Life vs. Stress plot can only be obtained by keeping one of the two stresses constant and varying the other one. Doing so will yield the straight line described by the above equation, where the term for the stress which is kept at a fixed value becomes another constant (in addition to the
This is the Arrhenius equation and it is plotted on a log-reciprocal scale. When the thermal stress is kept constant, then the linearized T-NT relationship becomes:
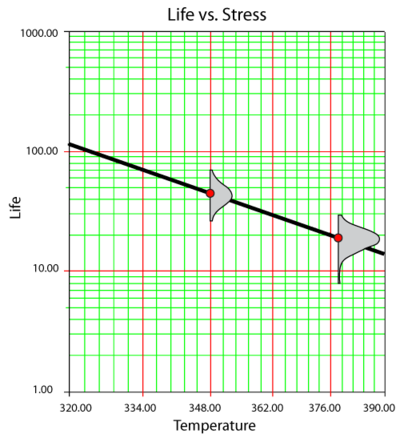
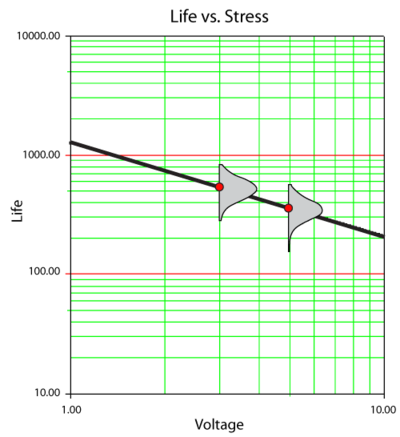
This is the inverse power law equation and it is plotted on a log-log scale. In the next two figures, data obtained from a temperature and voltage test were analyzed and plotted on a log-reciprocal scale. In the first figure, life is plotted versus temperature, with voltage held at a fixed value. In the second figure, life is plotted versus voltage, with temperature held at a fixed value.
A look at the Parameters B and n
Depending on which stress type is kept constant, it can be seen from the linearized T-NT relationship that either the parameter
Acceleration Factor
The acceleration factor for the T-NT relationship is given by:
where:
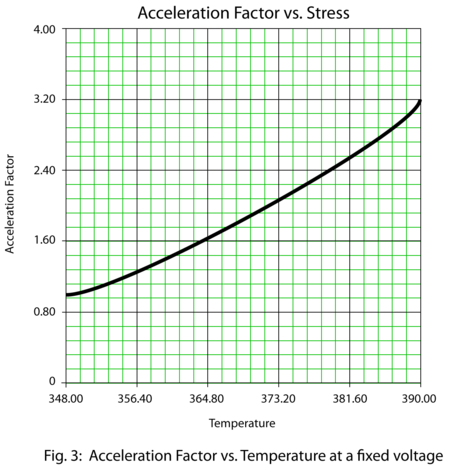
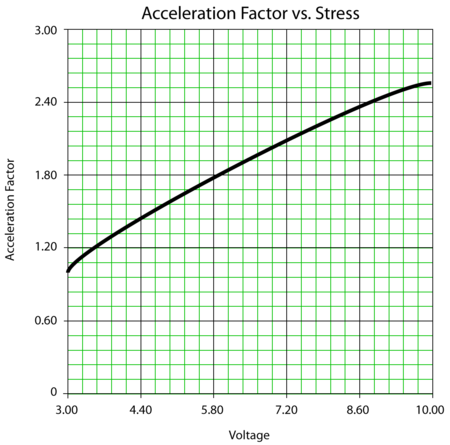
The acceleration factor is plotted versus stress in the same manner used to create the Life vs. Stress plots. That is, one stress type is kept constant and the other is varied.
T-NT Exponential
By setting
T-NT Exponential Statistical Properties Summary
Mean or MTTF
The mean,
Median
The median,
Mode
The mode,
Standard Deviation
The standard deviation,
T-NT Exponential Reliability Function
The T-NT exponential reliability function is given by:
This function is the complement of the T-NT exponential cumulative distribution function or:
and,
Conditional Reliability
The conditional reliability function for the T-NT exponential model is given by,
Reliable Life
For the T-NT exponential model, the reliable life, or the mission duration for a desired reliability goal,
- or:
Parameter Estimation
Maximum Likelihood Estimation Method
Substituting the T-NT relationship into the exponential log-likelihood equation yields:
where:
and:
The solution (parameter estimates) will be found by solving for the parameters
T-NT Weibull
By setting
T-NT Weibull Statistical Properties Summary
Mean or MTTF
The mean,
where
Median
The median,
Mode
The mode,
Standard Deviation
The standard deviation,
T-NT Weibull Reliability Function
The T-NT Weibull reliability function is given by:
Conditional Reliability Function
The T-NT Weibull conditional reliability function at a specified stress level is given by:
or:
Reliable Life
For the T-NT Weibull model, the reliable life,
T-NT Weibull Failure Rate Function
The T-NT Weibull failure rate function,
Parameter Estimation
Maximum Likelihood Estimation Method
Substituting the T-NT relationship into the Weibull log-likelihood function yields:
where:
and:
The solution (parameter estimates) will be found by solving for the parameters
T-NT Lognormal
The pdf of the lognormal distribution is given by:
where:
and:
The median of the lognormal distribution is given by:
The T-NT lognormal model pdf can be obtained by setting
or:
Thus:
Substituting the above equation into the lognormal pdf yields the T-NT lognormal model pdf or:
T-N-T Lognormal Statistical Properties Summary
The Mean
The mean life of the T-NT lognormal model (mean of the times-to-failure),
The mean of the natural logarithms of the times-to-failure,
The Standard Deviation
The standard deviation of the T-NT lognormal model (standard deviation of the times-to-failure),
The standard deviation of the natural logarithms of the times-to-failure,
The Mode
The mode of the T-NT lognormal model is given by:
T-NT Lognormal Reliability
For the T-NT lognormal model, the reliability for a mission of time
or:
Reliable Life
For the T-NT lognormal model, the reliable life, or the mission duration for a desired reliability goal,
where:
and:
Since
Lognormal Failure Rate
The T-NT lognormal failure rate is given by:
Parameter Estimation
Maximum Likelihood Estimation Method
The complete T-NT lognormal log-likelihood function is:
where:
and:
The solution (parameter estimates) will be found by solving for
T-NT Lognormal Example
12 electronic devices were put into a continuous accelerated life test and the following data were collected.
Using ALTA and the T-NT lognormal model, the following parameters were obtained:
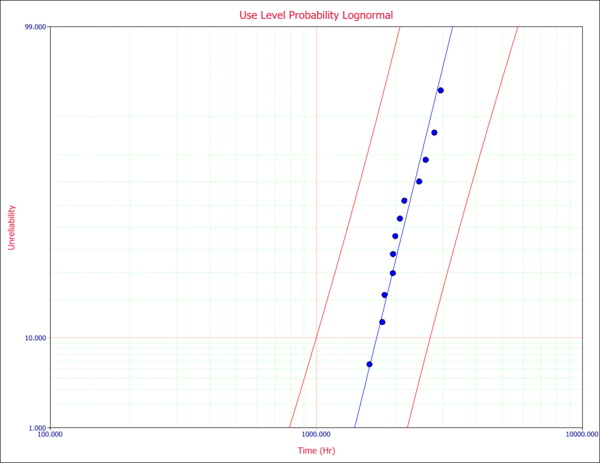
A probability plot, with the 2-sided 90% confidence bounds for the use stress levels of 323K and 2V, is shown next.
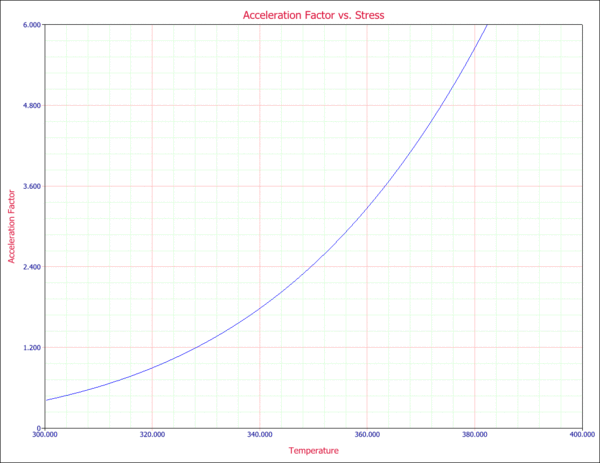
An acceleration factor plot, in which one of the stresses must be kept constant, can also be obtained. For example, in the following plot, the acceleration factor is plotted versus temperature given a constant voltage of 2V.
T-NT Confidence Bounds
Approximate Confidence Bounds for the T-NT Exponential
Confidence Bounds on the Mean Life
The mean life for the T-NT model is given by setting
where
If
or:
The variances and covariance of
where:
Confidence Bounds on Reliability
The bounds on reliability at a given time,
Confidence Bounds on Time
The bounds on time for a given reliability (ML estimate of time) are estimated by first solving the reliability function with respect to time:
The corresponding confidence bounds are estimated from:
Approximate Confidence Bounds for the T-NT Weibull
Bounds on the Parameters
Using the same approach as previously discussed (
and:
The variances and covariances of
where:
Confidence Bounds on Reliability
The reliability function (ML estimate) for the T-NT Weibull model is given by:
or:
Setting:
or:
The reliability function now becomes:
The next step is to find the upper and lower bounds on
where:
or:
The upper and lower bounds on reliability are:
Confidence Bounds on Time
The bounds on time (ML estimate of time) for a given reliability are estimated by first solving the reliability function with respect to time as follows:
or:
where
The upper and lower bounds on
where:
or:
The upper and lower bounds on time are then found by:
Approximate Confidence Bounds for the T-NT Lognormal
Bounds on the Parameters
Since the standard deviation,
and:
The lower and upper bounds on
and:
The variances and covariances of
- where:
Bounds on Reliability
The reliability of the lognormal distribution is given by:
Let
The above equation then becomes:
The bounds on
where:
or:
The upper and lower bounds on reliability are:
Confidence Bounds on Time
The bounds around time for a given lognormal percentile (unreliability) are estimated by first solving the reliability equation with respect to time, as follows:
where:
and:
The next step is to calculate the variance of
or:
The upper and lower bounds are then found by:
Solving for
When temperature and a second non-thermal stress (e.g., voltage) are the accelerated stresses of a test, then the Arrhenius and the inverse power law relationships can be combined to yield the Temperature-NonThermal (T-NT) relationship. This relationship is given by:
where:
The T-NT relationship can be linearized and plotted on a Life vs. Stress plot. The relationship is linearized by taking the natural logarithm of both sides in the T-NT relationship or:
Since life is now a function of two stresses, a Life vs. Stress plot can only be obtained by keeping one of the two stresses constant and varying the other one. Doing so will yield the straight line described by the above equation, where the term for the stress which is kept at a fixed value becomes another constant (in addition to the
This is the Arrhenius equation and it is plotted on a log-reciprocal scale. When the thermal stress is kept constant, then the linearized T-NT relationship becomes:
This is the inverse power law equation and it is plotted on a log-log scale. In the next two figures, data obtained from a temperature and voltage test were analyzed and plotted on a log-reciprocal scale. In the first figure, life is plotted versus temperature, with voltage held at a fixed value. In the second figure, life is plotted versus voltage, with temperature held at a fixed value.
A look at the Parameters B and n
Depending on which stress type is kept constant, it can be seen from the linearized T-NT relationship that either the parameter
Acceleration Factor
The acceleration factor for the T-NT relationship is given by:
where:
The acceleration factor is plotted versus stress in the same manner used to create the Life vs. Stress plots. That is, one stress type is kept constant and the other is varied.
T-NT Exponential
By setting
T-NT Exponential Statistical Properties Summary
Mean or MTTF
The mean,
Median
The median,
Mode
The mode,
Standard Deviation
The standard deviation,
T-NT Exponential Reliability Function
The T-NT exponential reliability function is given by:
This function is the complement of the T-NT exponential cumulative distribution function or:
and,
Conditional Reliability
The conditional reliability function for the T-NT exponential model is given by,
Reliable Life
For the T-NT exponential model, the reliable life, or the mission duration for a desired reliability goal,
- or:
Parameter Estimation
Maximum Likelihood Estimation Method
Substituting the T-NT relationship into the exponential log-likelihood equation yields:
where:
and:
The solution (parameter estimates) will be found by solving for the parameters
T-NT Weibull
By setting
T-NT Weibull Statistical Properties Summary
Mean or MTTF
The mean,
where
Median
The median,
Mode
The mode,
Standard Deviation
The standard deviation,
T-NT Weibull Reliability Function
The T-NT Weibull reliability function is given by:
Conditional Reliability Function
The T-NT Weibull conditional reliability function at a specified stress level is given by:
or:
Reliable Life
For the T-NT Weibull model, the reliable life,
T-NT Weibull Failure Rate Function
The T-NT Weibull failure rate function,
Parameter Estimation
Maximum Likelihood Estimation Method
Substituting the T-NT relationship into the Weibull log-likelihood function yields:
where:
and:
The solution (parameter estimates) will be found by solving for the parameters
T-NT Lognormal
The pdf of the lognormal distribution is given by:
where:
and:
The median of the lognormal distribution is given by:
The T-NT lognormal model pdf can be obtained by setting
or:
Thus:
Substituting the above equation into the lognormal pdf yields the T-NT lognormal model pdf or:
T-N-T Lognormal Statistical Properties Summary
The Mean
The mean life of the T-NT lognormal model (mean of the times-to-failure),
The mean of the natural logarithms of the times-to-failure,
The Standard Deviation
The standard deviation of the T-NT lognormal model (standard deviation of the times-to-failure),
The standard deviation of the natural logarithms of the times-to-failure,
The Mode
The mode of the T-NT lognormal model is given by:
T-NT Lognormal Reliability
For the T-NT lognormal model, the reliability for a mission of time
or:
Reliable Life
For the T-NT lognormal model, the reliable life, or the mission duration for a desired reliability goal,
where:
and:
Since
Lognormal Failure Rate
The T-NT lognormal failure rate is given by:
Parameter Estimation
Maximum Likelihood Estimation Method
The complete T-NT lognormal log-likelihood function is:
where:
and:
The solution (parameter estimates) will be found by solving for
T-NT Lognormal Example
12 electronic devices were put into a continuous accelerated life test and the following data were collected.
Using ALTA and the T-NT lognormal model, the following parameters were obtained:
A probability plot, with the 2-sided 90% confidence bounds for the use stress levels of 323K and 2V, is shown next.
An acceleration factor plot, in which one of the stresses must be kept constant, can also be obtained. For example, in the following plot, the acceleration factor is plotted versus temperature given a constant voltage of 2V.
T-NT Confidence Bounds
Approximate Confidence Bounds for the T-NT Exponential
Confidence Bounds on the Mean Life
The mean life for the T-NT model is given by setting
where
If
or:
The variances and covariance of
where:
Confidence Bounds on Reliability
The bounds on reliability at a given time,
Confidence Bounds on Time
The bounds on time for a given reliability (ML estimate of time) are estimated by first solving the reliability function with respect to time:
The corresponding confidence bounds are estimated from:
Approximate Confidence Bounds for the T-NT Weibull
Bounds on the Parameters
Using the same approach as previously discussed (
and:
The variances and covariances of
where:
Confidence Bounds on Reliability
The reliability function (ML estimate) for the T-NT Weibull model is given by:
or:
Setting:
or:
The reliability function now becomes:
The next step is to find the upper and lower bounds on
where:
or:
The upper and lower bounds on reliability are:
Confidence Bounds on Time
The bounds on time (ML estimate of time) for a given reliability are estimated by first solving the reliability function with respect to time as follows:
or:
where
The upper and lower bounds on
where:
or:
The upper and lower bounds on time are then found by:
Approximate Confidence Bounds for the T-NT Lognormal
Bounds on the Parameters
Since the standard deviation,
and:
The lower and upper bounds on
and:
The variances and covariances of
- where:
Bounds on Reliability
The reliability of the lognormal distribution is given by:
Let
The above equation then becomes:
The bounds on
where:
or:
The upper and lower bounds on reliability are:
Confidence Bounds on Time
The bounds around time for a given lognormal percentile (unreliability) are estimated by first solving the reliability equation with respect to time, as follows:
where:
and:
The next step is to calculate the variance of
or:
The upper and lower bounds are then found by:
Solving for