Template:Example:Eyring

Eyring Example

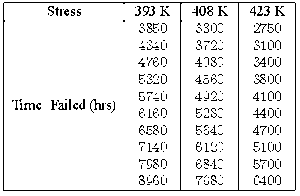
Consider the following times-to-failure data at three different stress levels.

Pdf of the lognormal distribution with different log-std values.

The data set was analyzed jointly and with a complete MLE solution over the entire data set using ReliaSoft's ALTA yielding:

[math]\displaystyle{ \widehat{\beta }=4.29186497 }[/math]

[math]\displaystyle{ }[/math]

[math]\displaystyle{ \widehat{B}=1454.08635742 }[/math]

Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323K using:

[math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right) }[/math]

or:

[math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align} }[/math]