Template:Example: Normal General Example Interval Data

Normal Distribution General Example Interval Data

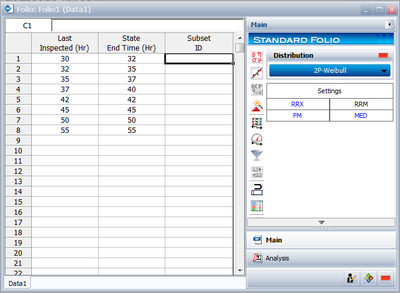
Eight units are being reliability tested and the following is a table of their times-to-failure:

Table - Non-Grouped Data Times-to-Failure with intervals (lnterval and left censored)
Data point index	Last Inspected	State End Time
1	30	32
2	32	35
3	35	37
4	37	40
5	42	42
6	45	45
7	50	50
8	55	55

Solution

This is a sequence of interval times-to-failure. This data set can be entered into Weibull++ by creating a data sheet that can be used to analyze times-to-failure data with interval and left censored data.

[math]\displaystyle{ }[/math]

The computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{align} & \widehat{\mu }= & 41.40 \\ & {{{\hat{\sigma }}}_{T}}= & 7.740. \end{align} }[/math]

For rank regression on x:

[math]\displaystyle{ \begin{align} & \widehat{\mu }= & 41.40 \\ & {{{\hat{\sigma }}}_{T}}= & 9.03. \end{align} }[/math]

For rank regression on y:

[math]\displaystyle{ \begin{align} & \widehat{\mu }= & 41.39 \\ & {{{\hat{\sigma }}}_{T}}= & 9.25. \end{align} }[/math]

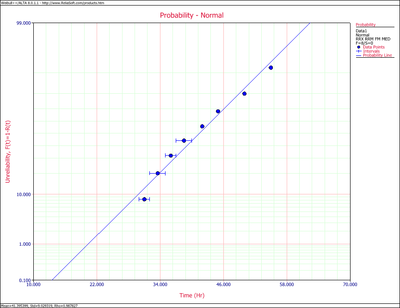
A plot of the MLE solution is shown next.

[math]\displaystyle{ }[/math]