Template:Effect of beta on the cdf

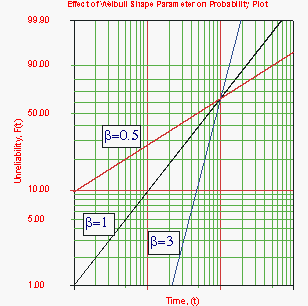
The Effect of β on the [math]\displaystyle{ cdf }[/math] and Reliability Function

Effect on [math]\displaystyle{ \beta }[/math] on the [math]\displaystyle{ cdf }[/math] on the Weibull probability plot with a fixed value of [math]\displaystyle{ \eta }[/math]

The above Figure shows the effect of the value of β on the [math]\displaystyle{ cdf }[/math], as manifested in the Weibull probability plot. It is easy to see why this parameter is sometimes referred to as the slope. Note that the models represented by the three lines all have the same value of η. Figure 6-3 shows the effects of these varied values of β on the reliability plot, which is a linear analog of the probability plot.

The effect of values of [math]\displaystyle{ \beta }[/math] on the Weibull reliability plot.

• R(t) decreases sharply and monotonically for 0 < β < 1 and is convex.
• For β = 1, R(t) decreases monotonically but less sharply than for 0 < β < 1 and is convex.
• For β > 1, R(t) decreases as increases. As wear-out sets in, the curve goes through an inflection point and decreases sharply.