Template:Aw characteristics: Difference between revisions
Chris Kahn (talk | contribs) |
|||
| Line 3: | Line 3: | ||
====Looking at <math>\beta </math>==== | ====Looking at <math>\beta </math>==== | ||
Beta | Beta (<math>\beta </math>) is called the shape parameter or slope of the Weibull distribution. Changing the value of <math>\beta </math> forces a change in the shape of the <math>pdf</math> as shown in the next figure. In addition, when the <math>cdf</math> is plotted on Weibull probability paper, a change in beta is a change in the slope of the distribution on Weibull probability paper. | ||
<br> | <br> | ||
'''Effects of <math>\beta </math> on the ''pdf''''' | '''Effects of <math>\beta </math> on the ''pdf''''' | ||
| Line 10: | Line 10: | ||
<br> | <br> | ||
<br> | <br> | ||
: | :* For <math>0<\beta <1</math> , the failure rate decreases with time and: | ||
:: | ::* As <math>T\to 0,</math> <math>f(T)\to \infty .</math> | ||
:: | ::* As <math>T\to \infty </math> , <math>f(T)\to 0</math> . | ||
:: | ::* <math>f(T)</math> decreases monotonically and is convex as <math>T</math> increases. | ||
:: | ::* The mode is non-existent. | ||
: | :* For <math>\beta =1,</math> it becomes the exponential distribution, as a special case, <br> | ||
<br> | <br> | ||
:or: | :or: | ||
| Line 23: | Line 23: | ||
:where <math>\tfrac{1}{\eta }=\lambda =</math> chance, useful life, or failure rate. | :where <math>\tfrac{1}{\eta }=\lambda =</math> chance, useful life, or failure rate. | ||
<br> | <br> | ||
: | :* For <math>\beta >1</math> , <math>f(T),</math> the Weibull assumes wear-out type shapes (i.e. the failure rate increases with time) and: | ||
:: | ::* <math>f(T)=0</math> at <math>T=0</math> . | ||
:: | ::* <math>f(T)</math> increases as <math>T\to \tilde{T}</math> (mode) and decreases thereafter. | ||
:: | ::* For <math>\beta =2</math> it becomes the Rayleigh distribution as a special case. For <math>\beta <2.6</math> the Weibull <math>pdf</math> is positively skewed (has a right tail), for <math>2.6<\beta <3.7</math> its coefficient of skewness approaches zero (no tail); consequently, it may approximate the normal <math>pdf</math> , and for <math>\beta >3.7</math> it is negatively skewed (left tail). | ||
: | :* The parameter <math>\beta </math> is a pure number, i.e. it is dimensionless. | ||
<br> | <br> | ||
| Line 38: | Line 38: | ||
<br> | <br> | ||
: | :* <math>R(T)</math> decreases sharply and monotonically for <math>0<\beta <1</math> , it is convex, and decreases less sharply for the same <math>\beta </math> . | ||
: | :* For <math>\beta =1</math> and the same <math>\eta </math> , <math>R(T)</math> decreases monotonically but less sharply than for <math>0<\beta <1</math> , and is convex. | ||
: | :* For <math>\beta >1</math> , <math>R(T)</math> decreases as <math>T</math> increases but less sharply than before, and as wear-out sets in, it decreases sharply and goes through an inflection point. | ||
<br> | <br> | ||
| Line 47: | Line 47: | ||
[[Image:ALTA4.6.gif|thumb|center|400px|Weibull Failure Rate vs. Time with <math>0<\Beta<1 </math>, <math>\Beta=1 </math>, <math>\Beta>1 </math>.]] | [[Image:ALTA4.6.gif|thumb|center|400px|Weibull Failure Rate vs. Time with <math>0<\Beta<1 </math>, <math>\Beta=1 </math>, <math>\Beta>1 </math>.]] | ||
<br> | <br> | ||
: | :* The Weibull failure rate for <math>0<\beta <1</math> is unbounded at <math>T=0</math> . The failure rate, <math>\lambda (T),</math> decreases thereafter monotonically and is convex, approaching the value of zero as <math>T\to \infty </math> or <math>\lambda (\infty )=0</math> . This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When such behavior is encountered, one or more of the following conclusions can be drawn: | ||
:: | ::* Burn-in testing and/or environmental stress screening are not well implemented. | ||
:: | ::* There are problems in the production line. | ||
:: | ::* Inadequate quality control. | ||
:: | ::* Packaging and transit problems. | ||
: | :* For <math>\beta =1</math> , <math>\lambda (T)</math> yields a constant value of <math>\tfrac{1}{\eta }</math> , or: | ||
::<math>\lambda (T)=\lambda =\frac{1}{\eta }</math> | ::<math>\lambda (T)=\lambda =\frac{1}{\eta }</math> | ||
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units. | This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units. | ||
: | :* For <math>\beta >1</math> , <math>\lambda (T)</math> increases as <math>T</math> increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For <math>1<\beta <2</math> the <math>\lambda (T)</math> curve is concave, consequently the failure rate increases at a decreasing rate as <math>T</math> increases. | ||
: | :* For <math>\beta =2</math> , or for the Rayleigh distribution case, the failure rate function is given by: | ||
::<math>\lambda (T)=\frac{2}{\eta }\left( \frac{T}{\eta } \right)</math> | ::<math>\lambda (T)=\frac{2}{\eta }\left( \frac{T}{\eta } \right)</math> | ||
<br> | <br> | ||
hence there emerges a straight line relationship between <math>\lambda (T)</math> and <math>T</math> , starting at a value of <math>\lambda (T)=0</math> at <math>T=0</math> , and increasing thereafter with a slope of <math>\tfrac{2}{{{\eta }^{2}}}</math> . Consequently, the failure rate increases at a constant rate as <math>T</math> increases. Furthermore, if <math>\eta =1</math> the slope becomes equal to 2, and <math>\lambda (T)</math> becomes a straight line which passes through the origin with a slope of 2. | hence there emerges a straight line relationship between <math>\lambda (T)</math> and <math>T</math> , starting at a value of <math>\lambda (T)=0</math> at <math>T=0</math> , and increasing thereafter with a slope of <math>\tfrac{2}{{{\eta }^{2}}}</math> . Consequently, the failure rate increases at a constant rate as <math>T</math> increases. Furthermore, if <math>\eta =1</math> the slope becomes equal to 2, and <math>\lambda (T)</math> becomes a straight line which passes through the origin with a slope of 2. | ||
: | :* When <math>\beta >2</math> the <math>\lambda (T)</math> curve is convex, with its slope increasing as <math>T</math> increases. Consequently, the failure rate increases at an increasing rate as <math>T</math> increases, indicating wear-out life. | ||
<br> | <br> | ||
Revision as of 23:35, 6 March 2012
Characteristics
The characteristics of the 2-parameter Weibull distribution can be exemplified by examining the two parameters, beta, [math]\displaystyle{ \beta , }[/math] and eta, [math]\displaystyle{ \eta , }[/math] and the effect they have on the [math]\displaystyle{ pdf, }[/math] reliability and failure rate functions.
Looking at [math]\displaystyle{ \beta }[/math]
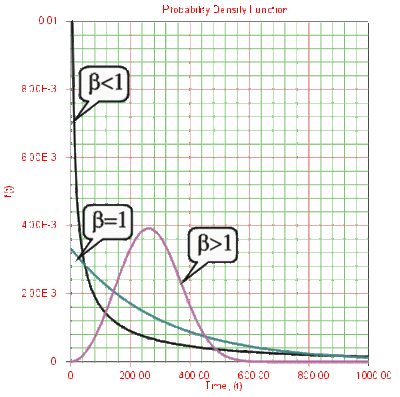
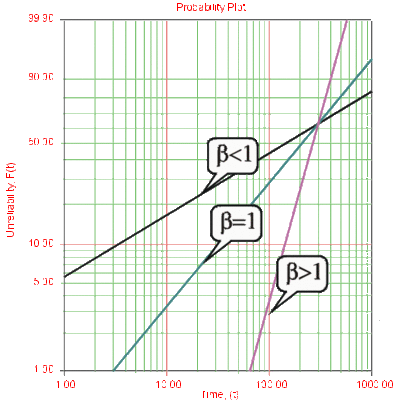
Beta ([math]\displaystyle{ \beta }[/math]) is called the shape parameter or slope of the Weibull distribution. Changing the value of [math]\displaystyle{ \beta }[/math] forces a change in the shape of the [math]\displaystyle{ pdf }[/math] as shown in the next figure. In addition, when the [math]\displaystyle{ cdf }[/math] is plotted on Weibull probability paper, a change in beta is a change in the slope of the distribution on Weibull probability paper.
Effects of [math]\displaystyle{ \beta }[/math] on the pdf
- For [math]\displaystyle{ 0\lt \beta \lt 1 }[/math] , the failure rate decreases with time and:
- As [math]\displaystyle{ T\to 0, }[/math] [math]\displaystyle{ f(T)\to \infty . }[/math]
- As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ f(T)\to 0 }[/math] .
- [math]\displaystyle{ f(T) }[/math] decreases monotonically and is convex as [math]\displaystyle{ T }[/math] increases.
- The mode is non-existent.
- For [math]\displaystyle{ \beta =1, }[/math] it becomes the exponential distribution, as a special case,
- or:
- [math]\displaystyle{ f(T)=\frac{1}{\eta }{{e}^{-\tfrac{T}{\eta }}};\text{ }\eta \gt 0,T\ge 0 }[/math]
- where [math]\displaystyle{ \tfrac{1}{\eta }=\lambda = }[/math] chance, useful life, or failure rate.
- For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ f(T), }[/math] the Weibull assumes wear-out type shapes (i.e. the failure rate increases with time) and:
- [math]\displaystyle{ f(T)=0 }[/math] at [math]\displaystyle{ T=0 }[/math] .
- [math]\displaystyle{ f(T) }[/math] increases as [math]\displaystyle{ T\to \tilde{T} }[/math] (mode) and decreases thereafter.
- For [math]\displaystyle{ \beta =2 }[/math] it becomes the Rayleigh distribution as a special case. For [math]\displaystyle{ \beta \lt 2.6 }[/math] the Weibull [math]\displaystyle{ pdf }[/math] is positively skewed (has a right tail), for [math]\displaystyle{ 2.6\lt \beta \lt 3.7 }[/math] its coefficient of skewness approaches zero (no tail); consequently, it may approximate the normal [math]\displaystyle{ pdf }[/math] , and for [math]\displaystyle{ \beta \gt 3.7 }[/math] it is negatively skewed (left tail).
- The parameter [math]\displaystyle{ \beta }[/math] is a pure number, i.e. it is dimensionless.
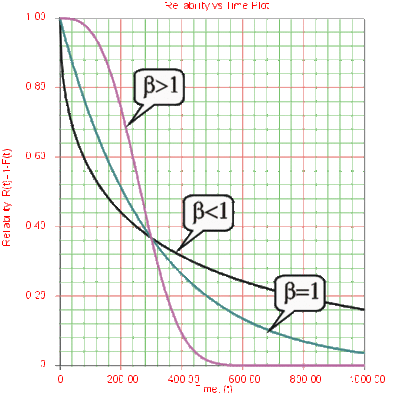
Effects of [math]\displaystyle{ \beta }[/math] on the Reliability Function and the cdf
- [math]\displaystyle{ R(T) }[/math] decreases sharply and monotonically for [math]\displaystyle{ 0\lt \beta \lt 1 }[/math] , it is convex, and decreases less sharply for the same [math]\displaystyle{ \beta }[/math] .
- For [math]\displaystyle{ \beta =1 }[/math] and the same [math]\displaystyle{ \eta }[/math] , [math]\displaystyle{ R(T) }[/math] decreases monotonically but less sharply than for [math]\displaystyle{ 0\lt \beta \lt 1 }[/math] , and is convex.
- For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ R(T) }[/math] decreases as [math]\displaystyle{ T }[/math] increases but less sharply than before, and as wear-out sets in, it decreases sharply and goes through an inflection point.
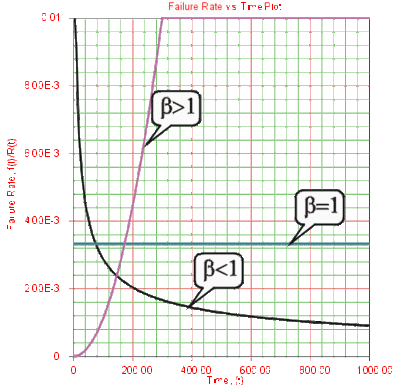
Effects of [math]\displaystyle{ \beta }[/math] on the Failure Rate Function
- The Weibull failure rate for [math]\displaystyle{ 0\lt \beta \lt 1 }[/math] is unbounded at [math]\displaystyle{ T=0 }[/math] . The failure rate, [math]\displaystyle{ \lambda (T), }[/math] decreases thereafter monotonically and is convex, approaching the value of zero as [math]\displaystyle{ T\to \infty }[/math] or [math]\displaystyle{ \lambda (\infty )=0 }[/math] . This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When such behavior is encountered, one or more of the following conclusions can be drawn:
- Burn-in testing and/or environmental stress screening are not well implemented.
- There are problems in the production line.
- Inadequate quality control.
- Packaging and transit problems.
- For [math]\displaystyle{ \beta =1 }[/math] , [math]\displaystyle{ \lambda (T) }[/math] yields a constant value of [math]\displaystyle{ \tfrac{1}{\eta } }[/math] , or:
- [math]\displaystyle{ \lambda (T)=\lambda =\frac{1}{\eta } }[/math]
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
- For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ \lambda (T) }[/math] increases as [math]\displaystyle{ T }[/math] increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For [math]\displaystyle{ 1\lt \beta \lt 2 }[/math] the [math]\displaystyle{ \lambda (T) }[/math] curve is concave, consequently the failure rate increases at a decreasing rate as [math]\displaystyle{ T }[/math] increases.
- For [math]\displaystyle{ \beta =2 }[/math] , or for the Rayleigh distribution case, the failure rate function is given by:
- [math]\displaystyle{ \lambda (T)=\frac{2}{\eta }\left( \frac{T}{\eta } \right) }[/math]
hence there emerges a straight line relationship between [math]\displaystyle{ \lambda (T) }[/math] and [math]\displaystyle{ T }[/math] , starting at a value of [math]\displaystyle{ \lambda (T)=0 }[/math] at [math]\displaystyle{ T=0 }[/math] , and increasing thereafter with a slope of [math]\displaystyle{ \tfrac{2}{{{\eta }^{2}}} }[/math] . Consequently, the failure rate increases at a constant rate as [math]\displaystyle{ T }[/math] increases. Furthermore, if [math]\displaystyle{ \eta =1 }[/math] the slope becomes equal to 2, and [math]\displaystyle{ \lambda (T) }[/math] becomes a straight line which passes through the origin with a slope of 2.
- When [math]\displaystyle{ \beta \gt 2 }[/math] the [math]\displaystyle{ \lambda (T) }[/math] curve is convex, with its slope increasing as [math]\displaystyle{ T }[/math] increases. Consequently, the failure rate increases at an increasing rate as [math]\displaystyle{ T }[/math] increases, indicating wear-out life.
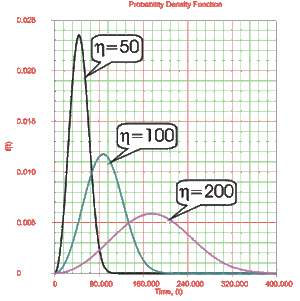
Looking at [math]\displaystyle{ \eta }[/math]
Eta, [math]\displaystyle{ \eta , }[/math] is called the scale parameter of the Weibull distribution. The parameter [math]\displaystyle{ \eta }[/math] has the same units as [math]\displaystyle{ T }[/math] , such as hours, miles, cycles, actuations, etc.
- • A change in the scale parameter [math]\displaystyle{ \eta }[/math] has the same effect on the distribution as a change of the abscissa scale.
- o If [math]\displaystyle{ \eta }[/math] is increased while [math]\displaystyle{ \beta }[/math] is kept the same, the distribution gets stretched out to the right and its height decreases, while maintaining its shape and location.
- o If [math]\displaystyle{ \eta }[/math] is decreased while [math]\displaystyle{ \beta }[/math] is kept the same, the distribution gets pushed in toward the left (i.e. toward its beginning, or 0) and its height increases.