Template:2 parameter exponential distribution RRY example

Example 2: 2 Parameter Exponential Distribution RRY

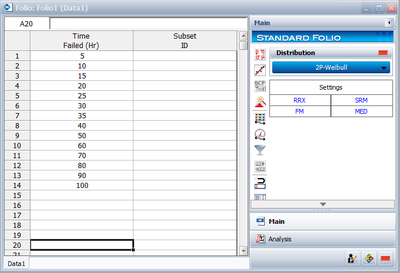
Fourteen units were being reliability tested and the following life test data were obtained (Table 7.1):

Table 7.1 - Life Test Data
Data point index	Time-to-failure
1	5
2	10
3	15
4	20
5	25
6	30
7	35
8	40
9	50
10	60
11	70
12	80
13	90
14	100

Assuming that the data follow a two-parameter exponential distribution, estimate the parameters and determine the correlation coefficient, [math]\displaystyle{ \rho }[/math], using rank regression on Y.

Solution to Example 2

Construct Table 7.2, as shown next.

[math]\displaystyle{ \overset{{}}{\mathop{\text{Table 7}\text{.2 - Least Squares Analysis}}}\, }[/math] [math]\displaystyle{ \begin{matrix} N & T_{i} & F(t_{i}) & y_{i} & T_{i}^{2} & y_{i}^{2} & T_{i} y_{i} \\ \text{1} & \text{5} & \text{0}\text{.0483} & \text{-0}\text{.0495} & \text{25} & \text{0}\text{.0025} & \text{-0}\text{.2475} \\ \text{2} & \text{10} & \text{0}\text{.1170} & \text{-0}\text{.1244} & \text{100} & \text{0}\text{.0155} & \text{-1}\text{.2443} \\ \text{3} & \text{15} & \text{0}\text{.1865} & \text{-0}\text{.2064} & \text{225} & \text{0}\text{.0426} & \text{-3}\text{.0961} \\ \text{4} & \text{20} & \text{0}\text{.2561} & \text{-0}\text{.2958} & \text{400} & \text{0}\text{.0875} & \text{-5}\text{.9170} \\ \text{5} & \text{25} & \text{0}\text{.3258} & \text{-0}\text{.3942} & \text{625} & \text{0}\text{.1554} & \text{-9}\text{.8557} \\ \text{6} & \text{30} & \text{0}\text{.3954} & \text{-0}\text{.5032} & \text{900} & \text{0}\text{.2532} & \text{-15}\text{.0956} \\ \text{7} & \text{35} & \text{0}\text{.4651} & \text{-0}\text{.6257} & \text{1225} & \text{0}\text{.3915} & \text{-21}\text{.8986} \\ \text{8} & \text{40} & \text{0}\text{.5349} & \text{-0}\text{.7655} & \text{1600} & \text{0}\text{.5860} & \text{-30}\text{.6201} \\ \text{9} & \text{50} & \text{0}\text{.6046} & \text{-0}\text{.9279} & \text{2500} & \text{0}\text{.8609} & \text{-46}\text{.3929} \\ \text{10} & \text{60} & \text{0}\text{.6742} & \text{-1}\text{.1215} & \text{3600} & \text{1}\text{.2577} & \text{-67}\text{.2883} \\ \text{11} & \text{70} & \text{0}\text{.7439} & \text{-1}\text{.3622} & \text{4900} & \text{1}\text{.8456} & \text{-95}\text{.3531} \\ \text{12} & \text{80} & \text{0}\text{.8135} & \text{-1}\text{.6793} & \text{6400} & \text{2}\text{.8201} & \text{-134}\text{.3459} \\ \text{13} & \text{90} & \text{0}\text{.8830} & \text{-2}\text{.1456} & \text{8100} & \text{4}\text{.6035} & \text{-193}\text{.1023} \\ \text{14} & \text{100} & \text{0}\text{.9517} & \text{-3}\text{.0303} & \text{10000} & \text{9}\text{.1829} & \text{-303}\text{.0324} \\ \sum_{}^{} & \text{630} & {} & \text{-13}\text{.2315} & \text{40600} & \text{22}\text{.1148} & \text{-927}\text{.4899} \\ \end{matrix} }[/math]

The median rank values ( [math]\displaystyle{ F({{T}_{i}}) }[/math] ) can be found in rank tables or they can be estimated using the Quick Statistical Reference in Weibull++. Given the values in the table above, calculate [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math]:

[math]\displaystyle{ \begin{align} \hat{b}= & \frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}}{{y}_{i}}-(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}})(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}})/14}{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,T_{i}^{2}-{{(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}})}^{2}}/14} \\ \\ \hat{b}= & \frac{-927.4899-(630)(-13.2315)/14}{40,600-{{(630)}^{2}}/14} \end{align} }[/math]

or:

[math]\displaystyle{ \hat{b}=-0.02711 }[/math]

and:

[math]\displaystyle{ \hat{a}=\overline{y}-\hat{b}\overline{T}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{T}_{i}}}{N} }[/math]

or:

[math]\displaystyle{ \hat{a}=\frac{-13.2315}{14}-(-0.02711)\frac{630}{14}=0.2748 }[/math]

Therefore:

[math]\displaystyle{ \hat{\lambda }=-\hat{b}=-(-0.02711)=0.02711\text{ failures/hour} }[/math]

and:

[math]\displaystyle{ \hat{\gamma }=\frac{\hat{a}}{\hat{\lambda }}=\frac{0.2748}{0.02711} }[/math]

or:

[math]\displaystyle{ \hat{\gamma }=10.1365\text{ hours} }[/math]

Then:

[math]\displaystyle{ f(T)=(0.02711)\cdot {{e}^{-0.02711(T-10.136)}} }[/math]

The correlation coefficient can be estimated using equation for calculating the correlation coefficient:

[math]\displaystyle{ \hat{\rho }=-0.9679 }[/math]

This example can be repeated using Weibull++, choosing two-parameter exponential and rank regression on Y (RRY), as shown in the figure on the following page.

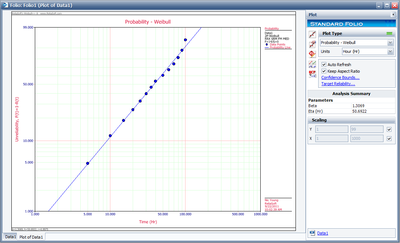
The estimated parameters and the correlation coefficient using Weibull++ were found to be:

[math]\displaystyle{ \hat{\lambda }=0.0271\text{ fr/hr },\hat{\gamma }=10.1348\text{ hr },\hat{\rho }=-0.9679 }[/math]

The probability plot can be obtained simply by clicking the Plot icon.