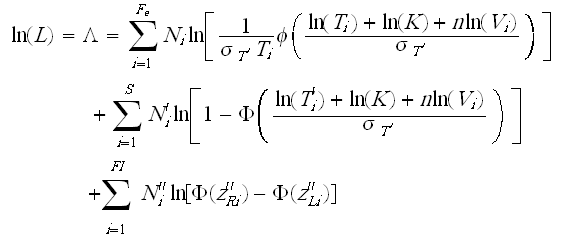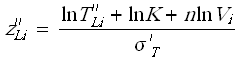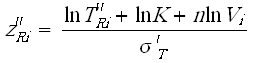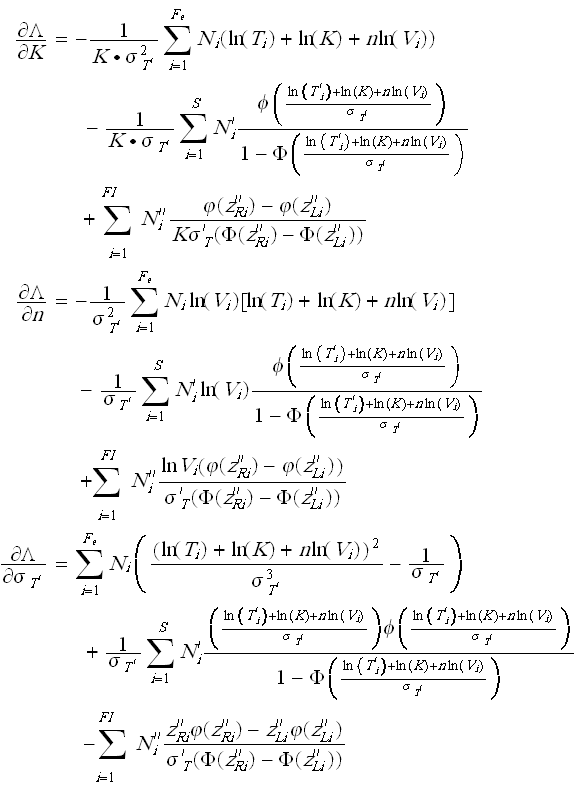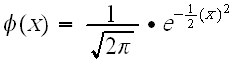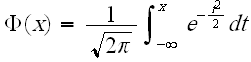Template:Ipl lognormal: Difference between revisions
No edit summary |
|||
| Line 5: | Line 5: | ||
The pdf of the lognormal distribution is given by: | The pdf of the lognormal distribution is given by: | ||
::<math>f(T)=\frac{}{} e^{-\frac{1}{2}(\frac{T'-\overline{T'}}{\sigma_{T'}}^2}</math> | ::<math>f(T)=\frac{}{} e^{-\frac{1}{2}(\frac{T'-\overline{T'}}{\sigma_{T'}})^2}</math> | ||
where: | where: | ||
:<math>T'=ln(T)</math> | ::<math>T'=ln(T)</math>. | ||
and: | |||
:<math>T</math> = times-to-failure. | :<math>T</math> = times-to-failure. | ||
| Line 20: | Line 22: | ||
The median of the lognormal distribution is given by: | The median of the lognormal distribution is given by: | ||
::<math>\breve{T}=e^{\overline{T}'}</math> | ::<math>\breve{T}=e^{\overline{T}'}</math> | ||
Revision as of 20:47, 15 February 2012
IPL-Lognormal
The pdf for the Inverse Power Law relationship and the lognormal distribution is given next.
The pdf of the lognormal distribution is given by:
- [math]\displaystyle{ f(T)=\frac{}{} e^{-\frac{1}{2}(\frac{T'-\overline{T'}}{\sigma_{T'}})^2} }[/math]
where:
- [math]\displaystyle{ T'=ln(T) }[/math].
and:
- [math]\displaystyle{ T }[/math] = times-to-failure.
- [math]\displaystyle{ \overline{T}' }[/math] = mean of the natural logarithms of the times-to-failure.
- [math]\displaystyle{ \sigma_{T'} }[/math] = standard deviation of the natural logarithms of the times-to-failure.
The median of the lognormal distribution is given by:
- [math]\displaystyle{ \breve{T}=e^{\overline{T}'} }[/math]
The IPL-lognormal model pdf can be obtained first by setting = L(V) in Eqn. ( 30). Therefore:
- [math]\displaystyle{ \breve{T}=L(V)=\frac{1}{K*V^n} }[/math]
or:
- [math]\displaystyle{ e^{\overline{T'}}=\frac{1}{K*V^n} }[/math]
Thus:
- [math]\displaystyle{ \overline{T}'=-ln(K)-n ln(V) }[/math](8)
Substituting Eqn. (8) into Eqn. (6) yields the IPL- lognormal model pdf or:
IPL-Lognormal Statistical Properties Summary
The Mean
The mean life of the IPL-lognormal model (mean of the times-to-failure), , is given by:
(9)
The mean of the natural logarithms of the times-to-failure, , in terms of and is given by:
The Standard Deviation
The standard deviation of the IPL-lognormal model (standard deviation of the times-to-failure), , is given by:
(10)
The standard deviation of the natural logarithms of the times-to-failure, , in terms of and is given by:
The Mode
The mode of the IPL-lognormal model is given by:
IPL-Lognormal Reliability
The reliability for a mission of time T, starting at age 0, for the IPL-lognormal model is determined by:
or:
Reliable Life
The reliable life, or the mission duration for a desired reliability goal, tR is estimated by first solving the reliability equation with respect to time, as follows:
where:
and:
Since = ln(T) the reliable life, tR, is given by:
Lognormal Failure Rate
The lognormal failure rate is given by:
Parameter Estimation
Maximum Likelihood Estimation Method
The complete IPL-lognormal log-likelihood function is:
where:
and:
- Fe is the number of groups of exact times-to-failure data points.
- Ni is the number of times-to-failure data points in the ith time-to-failure data group.
- [math]\displaystyle{ s_{T'} }[/math] is the standard deviation of the natural logarithm of the times-to-failure (unknown, the first of three parameters to be estimated).
- [math]\displaystyle{ K }[/math] is the IPL parameter (unknown, the second of three parameters to be estimated).
- [math]\displaystyle{ n }[/math] is the second IPL parameter (unknown, the third of three parameters to be estimated).
- [math]\displaystyle{ Vi }[/math] is the stress level of the ith group.
- [math]\displaystyle{ Ti }[/math] is the exact failure time of the ith group.
- [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
- [math]\displaystyle{ N'_i }[/math] is the number of suspensions in the ith group of suspension data points.
- [math]\displaystyle{ T^{'}_{i} }[/math] is the running time of the ith suspension data group.
- [math]\displaystyle{ FI }[/math] is the number of interval data groups.
- is the number of intervals in the ith group of data intervals.
- is the beginning of the ith interval.
- is the ending of the ith interval.
The solution (parameter estimates) will be found by solving for , , so that = 0, = 0 and = 0:
and: