Template:Characteristics of the exponential distribution alta: Difference between revisions
Jump to navigation
Jump to search
(Created page with '===Characteristics=== The characteristics of the 1-parameter exponential distribution can be exemplified by examining its parameter, lambda, <math>\lambda ,</math> and the effe…') |
|||
| Line 18: | Line 18: | ||
:• The 1-parameter exponential reliability function starts at the value of 1 at <math>T=0</math> . It decreases thereafter monotonically and is convex. | :• The 1-parameter exponential reliability function starts at the value of 1 at <math>T=0</math> . It decreases thereafter monotonically and is convex. | ||
:• As <math>T\to \infty </math> , <math>R(T\to \infty )\to 0</math>. | :• As <math>T\to \infty </math> , <math>R(T\to \infty )\to 0</math>. | ||
Effects of <math>\lambda </math> on the Failure Rate Function | ====Effects of <math>\lambda </math> on the Failure Rate Function==== | ||
The failure rate function for the exponential distribution is constant and it is equal to the parameter <math>\lambda </math> . | The failure rate function for the exponential distribution is constant and it is equal to the parameter <math>\lambda </math> . | ||
Revision as of 23:43, 6 February 2012
Characteristics
The characteristics of the 1-parameter exponential distribution can be exemplified by examining its parameter, lambda, [math]\displaystyle{ \lambda , }[/math] and the effect lambda has on the [math]\displaystyle{ pdf }[/math] , reliability and failure rate functions.
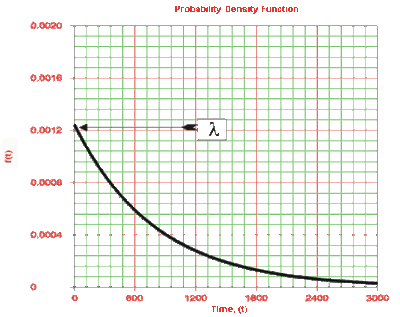
Effects of [math]\displaystyle{ \lambda }[/math] on the pdf
- • The scale parameter is [math]\displaystyle{ \tfrac{1}{\lambda } }[/math] .
- • As [math]\displaystyle{ \lambda }[/math] is decreased in value, the distribution is stretched out to the right, and as [math]\displaystyle{ \lambda }[/math] is increased, the distribution is pushed toward the origin.
- • This distribution has no shape parameter as it has only one shape, i.e. the exponential. The only parameter it has is the failure rate, [math]\displaystyle{ \lambda }[/math] .
- • The distribution starts at [math]\displaystyle{ T=0 }[/math] at the level of [math]\displaystyle{ f(T=0)=\lambda }[/math] and decreases thereafter exponentially and monotonically as [math]\displaystyle{ T }[/math] increases, and is convex.
- • As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ f(T)\to 0 }[/math].
- • This [math]\displaystyle{ pdf }[/math] can be thought of as a special case of the Weibull [math]\displaystyle{ pdf }[/math] with [math]\displaystyle{ \beta =1 }[/math] .
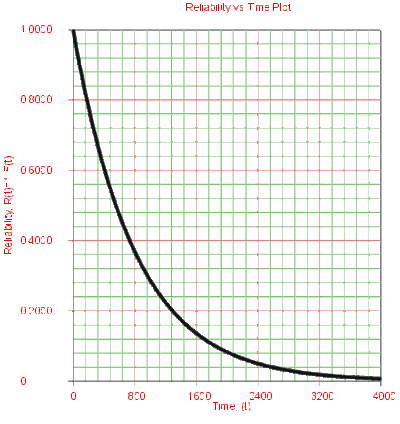
Effects of [math]\displaystyle{ \lambda }[/math] on the Reliability Function
- • The 1-parameter exponential reliability function starts at the value of 1 at [math]\displaystyle{ T=0 }[/math] . It decreases thereafter monotonically and is convex.
- • As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ R(T\to \infty )\to 0 }[/math].
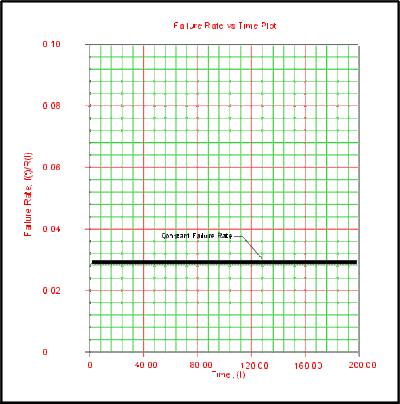
Effects of [math]\displaystyle{ \lambda }[/math] on the Failure Rate Function
The failure rate function for the exponential distribution is constant and it is equal to the parameter [math]\displaystyle{ \lambda }[/math] .