Template:Analysis of non-homogeneous warranty data: Difference between revisions
(Created page with '===Analysis of Non-Homogeneous Warranty Data=== In the previous sections and examples it is important to note that the underlying assumption was that the population was homogeneo…') |
|||
| Line 2: | Line 2: | ||
In the previous sections and examples it is important to note that the underlying assumption was that the population was homogeneous. In other words, all sold and returned units were exactly the same, i.e. the same population with no design changes and/or modifications. In many situations, as the product matures, design changes are made to enhance and/or improve the reliability of the product. Obviously, an improved product will exhibit different failure characteristics than its predecessor. To analyze such cases, where the population is non-homogeneous, one needs to extract each homogenous group, fit a life model to each group and then project the expected returns for each group based on the number of units at risk for each specific group. | In the previous sections and examples it is important to note that the underlying assumption was that the population was homogeneous. In other words, all sold and returned units were exactly the same, i.e. the same population with no design changes and/or modifications. In many situations, as the product matures, design changes are made to enhance and/or improve the reliability of the product. Obviously, an improved product will exhibit different failure characteristics than its predecessor. To analyze such cases, where the population is non-homogeneous, one needs to extract each homogenous group, fit a life model to each group and then project the expected returns for each group based on the number of units at risk for each specific group. | ||
'''Using IDs in Weibull++''' | |||
Weibull++ 7 uses the optional IDs column to differentiate between product versions or different designs (lots). Based on this entry, the data are then automatically separated and the parameters for each lot computed. Based on the computed parameters, failure projections can then be obtained. Note that it is important to realize that the same limitations as discussed previously, with regards to the number of failures that are needed, are also applicable here. In other words, distributions can be automatically fitted to lots that have return (failure) data, whereas if no returns have been experienced yet (either because the units are going to be introduced in the future or because no failures happened yet), the user will be asked to specify the parameters, since they can not be computed. Consequently, subsequent estimation/predictions related to these lots would be based on the user specified parameters. Following is an example that illustrates the use of IDs. | Weibull++ 7 uses the optional IDs column to differentiate between product versions or different designs (lots). Based on this entry, the data are then automatically separated and the parameters for each lot computed. Based on the computed parameters, failure projections can then be obtained. Note that it is important to realize that the same limitations as discussed previously, with regards to the number of failures that are needed, are also applicable here. In other words, distributions can be automatically fitted to lots that have return (failure) data, whereas if no returns have been experienced yet (either because the units are going to be introduced in the future or because no failures happened yet), the user will be asked to specify the parameters, since they can not be computed. Consequently, subsequent estimation/predictions related to these lots would be based on the user specified parameters. Following is an example that illustrates the use of IDs. | ||
'''Example 4:''' | |||
{{Example: Warranty Analysis Non-Homogeneous Data Example}} | |||
Revision as of 20:53, 21 February 2012
Analysis of Non-Homogeneous Warranty Data
In the previous sections and examples it is important to note that the underlying assumption was that the population was homogeneous. In other words, all sold and returned units were exactly the same, i.e. the same population with no design changes and/or modifications. In many situations, as the product matures, design changes are made to enhance and/or improve the reliability of the product. Obviously, an improved product will exhibit different failure characteristics than its predecessor. To analyze such cases, where the population is non-homogeneous, one needs to extract each homogenous group, fit a life model to each group and then project the expected returns for each group based on the number of units at risk for each specific group.
Using IDs in Weibull++
Weibull++ 7 uses the optional IDs column to differentiate between product versions or different designs (lots). Based on this entry, the data are then automatically separated and the parameters for each lot computed. Based on the computed parameters, failure projections can then be obtained. Note that it is important to realize that the same limitations as discussed previously, with regards to the number of failures that are needed, are also applicable here. In other words, distributions can be automatically fitted to lots that have return (failure) data, whereas if no returns have been experienced yet (either because the units are going to be introduced in the future or because no failures happened yet), the user will be asked to specify the parameters, since they can not be computed. Consequently, subsequent estimation/predictions related to these lots would be based on the user specified parameters. Following is an example that illustrates the use of IDs.
Example 4:
Warranty Analysis Non-Homogeneous Data Example
A company keeps track of its production and returns. The company uses the dates of failure format to record the data. For the product in question, three versions (A, B and C) have been produced and put in service. The in-service data is as follows (using the Month/Day/Year date format):
Furthermore, the following sales are forecast:
The return data are as follows. Note that in order to identify which lot each unit comes from, and to be able to compute its time-in-service, each return (failure) includes a return date, the date of when it was put in service and the model ID.
Assuming that the given information is current as of 5/1/2006, analyze the data using the lognormal distribution and MLE analysis method for all models (Model A, Model B, Model C), and provide a return forecast for the next ten months.
Solution
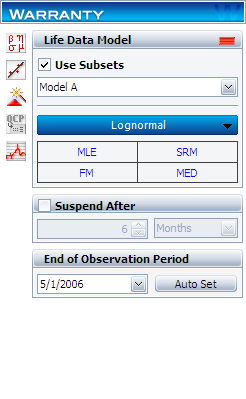
Create a warranty analysis folio and select the dates of failure format. Enter the data from the tables in the Sales, Returns and Future Sales sheets. On the control panel, select the Use Subsets check box, as shown next. This allows the software to separately analyze each subset of data. Use the drop-down list to switch between subset IDs and alter the analysis settings (use the lognormal distribution and MLE analysis method for all models).
In the End of Observation Period field, enter 5/1/2006, and then calculate the parameters. The results are:
Note that in this example, the same distribution and analysis method were assumed for each of the product models. If desired, different distribution types, analysis methods, confidence bounds methods, etc., can be assumed for each IDs.
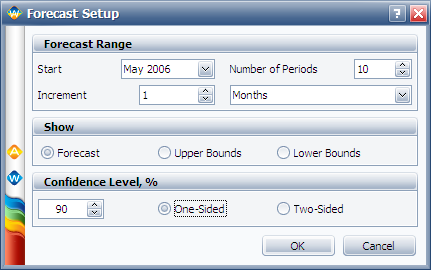
To obtain the expected failures for the next 10 months, click the Generate Forecast icon. In the Forecast Setup window, set the forecast to start on May 2, 2006 and set the number of forecast periods to 10. Set the increment (length of each period) to 1 Month, as shown next.
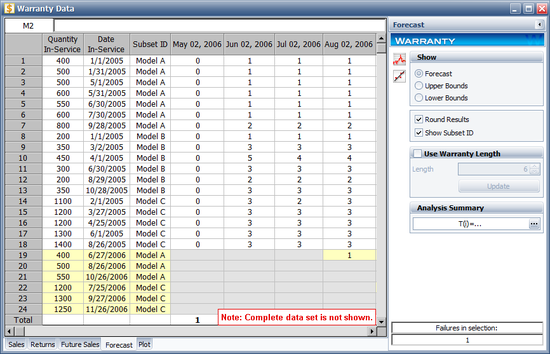
Click OK. A Forecast sheet will be created, with the predicted future returns. The following figure shows part of the Forecast sheet.
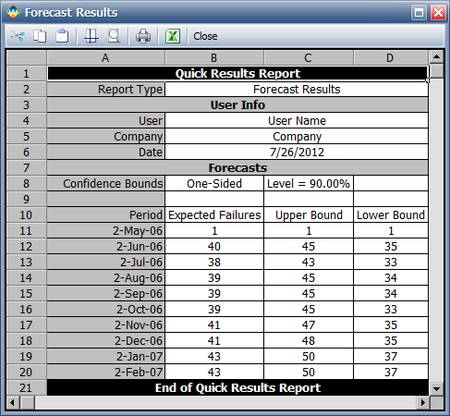
To view a summary of the analysis, click the Show Analysis Summary (...) button. The following figure shows the summary of the forecasted returns.
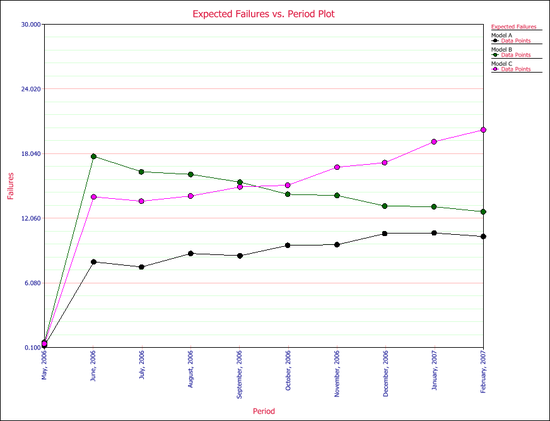
Click the Plot icon and choose the Expected Failures plot. The plot displays the predicted number of returns for each month, as shown next.