Template:Characteristics of the generalized gamma distribution: Difference between revisions
Jump to navigation
Jump to search
(Created page with '===Characteristics of the Generalized Gamma Distribution=== As mentioned previously, the generalized gamma distribution includes other distributions as special cases based on the…') |
|||
| Line 7: | Line 7: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& \beta = | & \beta = \frac{1}{\sigma } \\ | ||
& \eta = & \ln (\mu ) | & \eta = & \ln (\mu ) | ||
\end{align}</math> | \end{align}</math> | ||
Revision as of 21:47, 14 February 2012
Characteristics of the Generalized Gamma Distribution
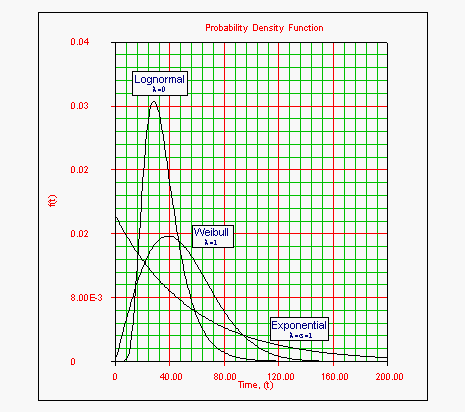
As mentioned previously, the generalized gamma distribution includes other distributions as special cases based on the values of the parameters.
- • The Weibull distribution is a special case when [math]\displaystyle{ \lambda =1 }[/math] and:
- [math]\displaystyle{ \begin{align} & \beta = \frac{1}{\sigma } \\ & \eta = & \ln (\mu ) \end{align} }[/math]
- • In this case, the generalized distribution has the same behavior as the Weibull for [math]\displaystyle{ \sigma \gt 1, }[/math] [math]\displaystyle{ \sigma =1, }[/math] and [math]\displaystyle{ \sigma \lt 1 }[/math] ( [math]\displaystyle{ \beta \lt 1, }[/math] [math]\displaystyle{ \beta =1, }[/math] and [math]\displaystyle{ \beta \gt 1 }[/math] respectively).
- • The exponential distribution is a special case when [math]\displaystyle{ \lambda =1 }[/math] and [math]\displaystyle{ \sigma =1 }[/math].
- • The lognormal distribution is a special case when [math]\displaystyle{ \lambda =0 }[/math].
- • The gamma distribution is a special case when [math]\displaystyle{ \lambda =\sigma }[/math].
By allowing [math]\displaystyle{ \lambda }[/math] to take negative values, the generalized gamma distribution can be further extended to include additional distributions as special cases. For example, the Fréchet distribution of maxima (also known as a reciprocal Weibull) is a special case when [math]\displaystyle{ \lambda =-1 }[/math].