The Weibull Distribution: Difference between revisions
| Line 13: | Line 13: | ||
{{Estimation of the Weibull Parameters}} | {{Estimation of the Weibull Parameters}} | ||
{{weibull fisher matrix confidence bounds}} | |||
== Likelihood Ratio Confidence Bounds == | == Likelihood Ratio Confidence Bounds == | ||
Revision as of 16:51, 4 January 2012
The Weibull Distribution
The Weibull distribution is one of the most widely used lifetime distributions in reliability engineering. It is a versatile distribution that can take on the characteristics of other types of distributions, based on the value of the shape parameter, [math]\displaystyle{ \boldsymbol{\beta} }[/math]. This chapter provides a brief background on the Weibull distribution, presents and derives most of the applicable equations and presents examples calculated both manually and by using ReliaSoft's Weibull++.
The Weibull Distribution
The Weibull distribution is one of the most widely used lifetime distributions in reliability engineering. It is a versatile distribution that can take on the characteristics of other types of distributions, based on the value of the shape parameter, [math]\displaystyle{ \boldsymbol{\beta} }[/math]. This chapter provides a brief background on the Weibull distribution, presents and derives most of the applicable equations and presents examples calculated both manually and by using ReliaSoft's Weibull++.
Template loop detected: Template:Weibull Probability Density Function
The Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} \,\! }[/math], (also called MTTF) of the Weibull pdf is given by:
- [math]\displaystyle{ \overline{T}=\gamma +\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
where
- [math]\displaystyle{ \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
is the gamma function evaluated at the value of:
- [math]\displaystyle{ \left( { \frac{1}{\beta }}+1\right) \,\! }[/math]
The gamma function is defined as:
- [math]\displaystyle{ \Gamma (n)=\int_{0}^{\infty }e^{-x}x^{n-1}dx \,\! }[/math]
For the 2-parameter case, this can be reduced to:
- [math]\displaystyle{ \overline{T}=\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
Note that some practitioners erroneously assume that [math]\displaystyle{ \eta \,\! }[/math] is equal to the MTTF, [math]\displaystyle{ \overline{T}\,\! }[/math]. This is only true for the case of: [math]\displaystyle{ \beta=1 \,\! }[/math] or:
- [math]\displaystyle{ \begin{align} \overline{T} &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {2}\right) \\ &= \eta \cdot 1\\ &= \eta \end{align} \,\! }[/math]
The Median
The median, [math]\displaystyle{ \breve{T}\,\! }[/math], of the Weibull distribution is given by:
- [math]\displaystyle{ \breve{T}=\gamma +\eta \left( \ln 2\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Mode
The mode, [math]\displaystyle{ \tilde{T} \,\! }[/math], is given by:
- [math]\displaystyle{ \tilde{T}=\gamma +\eta \left( 1-\frac{1}{\beta }\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Standard Deviation
The standard deviation, [math]\displaystyle{ \sigma _{T}\,\! }[/math], is given by:
- [math]\displaystyle{ \sigma _{T}=\eta \cdot \sqrt{\Gamma \left( {\frac{2}{\beta }}+1\right) -\Gamma \left( {\frac{1}{ \beta }}+1\right) ^{2}} \,\! }[/math]
The Weibull Reliability Function
The equation for the 3-parameter Weibull cumulative density function, cdf, is given by:
- [math]\displaystyle{ F(t)=1-e^{-\left( \frac{t-\gamma }{\eta }\right) ^{\beta }} \,\! }[/math]
This is also referred to as unreliability and designated as [math]\displaystyle{ Q(t) \,\! }[/math] by some authors.
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function for the 3-parameter Weibull distribution is then given by:
- [math]\displaystyle{ R(t)=e^{-\left( { \frac{t-\gamma }{\eta }}\right) ^{\beta }} \,\! }[/math]
The Weibull Conditional Reliability Function
The 3-parameter Weibull conditional reliability function is given by:
- [math]\displaystyle{ R(t|T)={ \frac{R(T+t)}{R(T)}}={\frac{e^{-\left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }}}{e^{-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }}}} \,\! }[/math]
or:
- [math]\displaystyle{ R(t|T)=e^{-\left[ \left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }\right] } \,\! }[/math]
These give the reliability for a new mission of [math]\displaystyle{ t \,\! }[/math] duration, having already accumulated [math]\displaystyle{ T \,\! }[/math] time of operation up to the start of this new mission, and the units are checked out to assure that they will start the next mission successfully. It is called conditional because you can calculate the reliability of a new mission based on the fact that the unit or units already accumulated hours of operation successfully.
The Weibull Reliable Life
The reliable life, [math]\displaystyle{ T_{R}\,\! }[/math], of a unit for a specified reliability, [math]\displaystyle{ R\,\! }[/math], starting the mission at age zero, is given by:
- [math]\displaystyle{ T_{R}=\gamma +\eta \cdot \left\{ -\ln ( R ) \right\} ^{ \frac{1}{\beta }} \,\! }[/math]
This is the life for which the unit/item will be functioning successfully with a reliability of [math]\displaystyle{ R\,\! }[/math]. If [math]\displaystyle{ R = 0.50\,\! }[/math], then [math]\displaystyle{ T_{R}=\breve{T} \,\! }[/math], the median life, or the life by which half of the units will survive.
The Weibull Failure Rate Function
The Weibull failure rate function, [math]\displaystyle{ \lambda(t) \,\! }[/math], is given by:
- [math]\displaystyle{ \lambda \left( t\right) = \frac{f\left( t\right) }{R\left( t\right) }=\frac{\beta }{\eta }\left( \frac{ t-\gamma }{\eta }\right) ^{\beta -1} \,\! }[/math]
The Weibull distribution is widely used in reliability and life data analysis due to its versatility. Depending on the values of the parameters, the Weibull distribution can be used to model a variety of life behaviors. We will now examine how the values of the shape parameter, [math]\displaystyle{ \beta\,\! }[/math], and the scale parameter, [math]\displaystyle{ \eta\,\! }[/math], affect such distribution characteristics as the shape of the curve, the reliability and the failure rate. Note that in the rest of this section we will assume the most general form of the Weibull distribution, (i.e., the 3-parameter form). The appropriate substitutions to obtain the other forms, such as the 2-parameter form where [math]\displaystyle{ \gamma = 0,\,\! }[/math] or the 1-parameter form where [math]\displaystyle{ \beta = C = \,\! }[/math] constant, can easily be made.
Effects of the Shape Parameter, beta
The Weibull shape parameter, [math]\displaystyle{ \beta\,\! }[/math], is also known as the slope. This is because the value of [math]\displaystyle{ \beta\,\! }[/math] is equal to the slope of the regressed line in a probability plot. Different values of the shape parameter can have marked effects on the behavior of the distribution. In fact, some values of the shape parameter will cause the distribution equations to reduce to those of other distributions. For example, when [math]\displaystyle{ \beta = 1\,\! }[/math], the pdf of the 3-parameter Weibull distribution reduces to that of the 2-parameter exponential distribution or:
- [math]\displaystyle{ f(t)={\frac{1}{\eta }}e^{-{\frac{t-\gamma }{\eta }}} \,\! }[/math]
where [math]\displaystyle{ \frac{1}{\eta }=\lambda = \,\! }[/math] failure rate. The parameter [math]\displaystyle{ \beta\,\! }[/math] is a pure number, (i.e., it is dimensionless). The following figure shows the effect of different values of the shape parameter, [math]\displaystyle{ \beta\,\! }[/math], on the shape of the pdf. As you can see, the shape can take on a variety of forms based on the value of [math]\displaystyle{ \beta\,\! }[/math].
For [math]\displaystyle{ 0\lt \beta \leq 1 \,\! }[/math]:
- As [math]\displaystyle{ t \rightarrow 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\! }[/math]), [math]\displaystyle{ f(t)\rightarrow \infty.\,\! }[/math]
- As [math]\displaystyle{ t\rightarrow \infty\,\! }[/math], [math]\displaystyle{ f(t)\rightarrow 0\,\! }[/math].
- [math]\displaystyle{ f(t)\,\! }[/math] decreases monotonically and is convex as it increases beyond the value of [math]\displaystyle{ \gamma\,\! }[/math].
- The mode is non-existent.
For [math]\displaystyle{ \beta \gt 1 \,\! }[/math]:
- [math]\displaystyle{ f(t) = 0\,\! }[/math] at [math]\displaystyle{ t = 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\! }[/math]).
- [math]\displaystyle{ f(t)\,\! }[/math] increases as [math]\displaystyle{ t\rightarrow \tilde{T} \,\! }[/math] (the mode) and decreases thereafter.
- For [math]\displaystyle{ \beta \lt 2.6\,\! }[/math] the Weibull pdf is positively skewed (has a right tail), for [math]\displaystyle{ 2.6 \lt \beta \lt 3.7\,\! }[/math] its coefficient of skewness approaches zero (no tail). Consequently, it may approximate the normal pdf, and for [math]\displaystyle{ \beta \gt 3.7\,\! }[/math] it is negatively skewed (left tail). The way the value of [math]\displaystyle{ \beta\,\! }[/math] relates to the physical behavior of the items being modeled becomes more apparent when we observe how its different values affect the reliability and failure rate functions. Note that for [math]\displaystyle{ \beta = 0.999\,\! }[/math], [math]\displaystyle{ f(0) = \infty\,\! }[/math], but for [math]\displaystyle{ \beta = 1.001\,\! }[/math], [math]\displaystyle{ f(0) = 0.\,\! }[/math] This abrupt shift is what complicates MLE estimation when [math]\displaystyle{ \beta\,\! }[/math] is close to 1.
The Effect of beta on the cdf and Reliability Function
The above figure shows the effect of the value of [math]\displaystyle{ \beta\,\! }[/math] on the cdf, as manifested in the Weibull probability plot. It is easy to see why this parameter is sometimes referred to as the slope. Note that the models represented by the three lines all have the same value of [math]\displaystyle{ \eta\,\! }[/math]. The following figure shows the effects of these varied values of [math]\displaystyle{ \beta\,\! }[/math] on the reliability plot, which is a linear analog of the probability plot.
- [math]\displaystyle{ R(t)\,\! }[/math] decreases sharply and monotonically for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] and is convex.
- For [math]\displaystyle{ \beta = 1\,\! }[/math], [math]\displaystyle{ R(t)\,\! }[/math] decreases monotonically but less sharply than for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] and is convex.
- For [math]\displaystyle{ \beta \gt 1\,\! }[/math], [math]\displaystyle{ R(t)\,\! }[/math] decreases as increases. As wear-out sets in, the curve goes through an inflection point and decreases sharply.
The Effect of beta on the Weibull Failure Rate
The value of [math]\displaystyle{ \beta\,\! }[/math] has a marked effect on the failure rate of the Weibull distribution and inferences can be drawn about a population's failure characteristics just by considering whether the value of [math]\displaystyle{ \beta\,\! }[/math] is less than, equal to, or greater than one.
As indicated by above figure, populations with [math]\displaystyle{ \beta \lt 1\,\! }[/math] exhibit a failure rate that decreases with time, populations with [math]\displaystyle{ \beta = 1\,\! }[/math] have a constant failure rate (consistent with the exponential distribution) and populations with [math]\displaystyle{ \beta \gt 1\,\! }[/math] have a failure rate that increases with time. All three life stages of the bathtub curve can be modeled with the Weibull distribution and varying values of [math]\displaystyle{ \beta\,\! }[/math]. The Weibull failure rate for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] is unbounded at [math]\displaystyle{ T = 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\!)\,\! }[/math]. The failure rate, [math]\displaystyle{ \lambda(t),\,\! }[/math] decreases thereafter monotonically and is convex, approaching the value of zero as [math]\displaystyle{ t\rightarrow \infty\,\! }[/math] or [math]\displaystyle{ \lambda (\infty) = 0\,\! }[/math]. This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When encountering such behavior in a manufactured product, it may be indicative of problems in the production process, inadequate burn-in, substandard parts and components, or problems with packaging and shipping. For [math]\displaystyle{ \beta = 1\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] yields a constant value of [math]\displaystyle{ { \frac{1}{\eta }} \,\! }[/math] or:
- [math]\displaystyle{ \lambda (t)=\lambda ={\frac{1}{\eta }} \,\! }[/math]
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
For [math]\displaystyle{ \beta \gt 1\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] increases as [math]\displaystyle{ t\,\! }[/math] increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For [math]\displaystyle{ 1 \lt \beta \lt 2,\,\! }[/math] the [math]\displaystyle{ \lambda(t)\,\! }[/math] curve is concave, consequently the failure rate increases at a decreasing rate as [math]\displaystyle{ t\,\! }[/math] increases.
For [math]\displaystyle{ \beta = 2\,\! }[/math] there emerges a straight line relationship between [math]\displaystyle{ \lambda(t)\,\! }[/math] and [math]\displaystyle{ t\,\! }[/math], starting at a value of [math]\displaystyle{ \lambda(t) = 0\,\! }[/math] at [math]\displaystyle{ t = \gamma\,\! }[/math], and increasing thereafter with a slope of [math]\displaystyle{ { \frac{2}{\eta ^{2}}} \,\! }[/math]. Consequently, the failure rate increases at a constant rate as [math]\displaystyle{ t\,\! }[/math] increases. Furthermore, if [math]\displaystyle{ \eta = 1\,\! }[/math] the slope becomes equal to 2, and when [math]\displaystyle{ \gamma = 0\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] becomes a straight line which passes through the origin with a slope of 2. Note that at [math]\displaystyle{ \beta = 2\,\! }[/math], the Weibull distribution equations reduce to that of the Rayleigh distribution.
When [math]\displaystyle{ \beta \gt 2,\,\! }[/math] the [math]\displaystyle{ \lambda(t)\,\! }[/math] curve is convex, with its slope increasing as [math]\displaystyle{ t\,\! }[/math] increases. Consequently, the failure rate increases at an increasing rate as [math]\displaystyle{ t\,\! }[/math] increases, indicating wearout life.
Effects of the Scale Parameter, eta
A change in the scale parameter [math]\displaystyle{ \eta\,\! }[/math] has the same effect on the distribution as a change of the abscissa scale. Increasing the value of [math]\displaystyle{ \eta\,\! }[/math] while holding [math]\displaystyle{ \beta\,\! }[/math] constant has the effect of stretching out the pdf. Since the area under a pdf curve is a constant value of one, the "peak" of the pdf curve will also decrease with the increase of [math]\displaystyle{ \eta\,\! }[/math], as indicated in the above figure.
- If [math]\displaystyle{ \eta\,\! }[/math] is increased while [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math] are kept the same, the distribution gets stretched out to the right and its height decreases, while maintaining its shape and location.
- If [math]\displaystyle{ \eta\,\! }[/math] is decreased while [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math] are kept the same, the distribution gets pushed in towards the left (i.e., towards its beginning or towards 0 or [math]\displaystyle{ \gamma\,\! }[/math]), and its height increases.
- [math]\displaystyle{ \eta\,\! }[/math] has the same units as [math]\displaystyle{ t\,\! }[/math], such as hours, miles, cycles, actuations, etc.
Effects of the Location Parameter, gamma
The location parameter, [math]\displaystyle{ \gamma\,\! }[/math], as the name implies, locates the distribution along the abscissa. Changing the value of [math]\displaystyle{ \gamma\,\! }[/math] has the effect of sliding the distribution and its associated function either to the right (if [math]\displaystyle{ \gamma \gt 0\,\! }[/math]) or to the left (if [math]\displaystyle{ \gamma \lt 0\,\! }[/math]).
- When [math]\displaystyle{ \gamma = 0,\,\! }[/math] the distribution starts at [math]\displaystyle{ t=0\,\! }[/math] or at the origin.
- If [math]\displaystyle{ \gamma \gt 0,\,\! }[/math] the distribution starts at the location [math]\displaystyle{ \gamma\,\! }[/math] to the right of the origin.
- If [math]\displaystyle{ \gamma \lt 0,\,\! }[/math] the distribution starts at the location [math]\displaystyle{ \gamma\,\! }[/math] to the left of the origin.
- [math]\displaystyle{ \gamma\,\! }[/math] provides an estimate of the earliest time-to-failure of such units.
- The life period 0 to [math]\displaystyle{ + \gamma\,\! }[/math] is a failure free operating period of such units.
- The parameter [math]\displaystyle{ \gamma\,\! }[/math] may assume all values and provides an estimate of the earliest time a failure may be observed. A negative [math]\displaystyle{ \gamma\,\! }[/math] may indicate that failures have occurred prior to the beginning of the test, namely during production, in storage, in transit, during checkout prior to the start of a mission, or prior to actual use.
- [math]\displaystyle{ \gamma\,\! }[/math] has the same units as [math]\displaystyle{ t\,\! }[/math], such as hours, miles, cycles, actuations, etc.
Template loop detected: Template:Estimation of the Weibull Parameters
Template loop detected: Template:Weibull fisher matrix confidence bounds
Likelihood Ratio Confidence Bounds
As covered in Chapter 5, the likelihood confidence bounds are calculated by finding values for θ1 and θ2 that satisfy:
- [math]\displaystyle{ -2\cdot \text{ln}\left( \frac{L(\theta _{1},\theta _{2})}{L(\hat{\theta }_{1}, \hat{\theta }_{2})}\right) =\chi _{\alpha ;1}^{2} EQNREF lratio2 }[/math]
This equation can be rewritten as:
- [math]\displaystyle{ L(\theta _{1},\theta _{2})=L(\hat{\theta }_{1},\hat{\theta } _{2})\cdot e^{\frac{-\chi _{\alpha ;1}^{2}}{2}} EQNREF lratio3 }[/math]
For complete data, the likelihood function for the Weibull distribution is given by:
- [math]\displaystyle{ L(\beta ,\eta )=\prod_{i=1}^{N}f(x_{i};\beta ,\eta )=\prod_{i=1}^{N}\frac{ \beta }{\eta }\cdot \left( \frac{x_{i}}{\eta }\right) ^{\beta -1}\cdot e^{-\left( \frac{x_{i}}{\eta }\right) ^{\beta }} }[/math]
For a given value of α, values for β and η can be found which represent the maximum and minimum values that satisfy Eqn. (\ref {lratio3}). These represent the confidence bounds for the parameters at a confidence level δ, where α = δ for two-sided bounds and α = 2δ − 1 for one-sided.
Similarly, the bounds on time and reliability can be found by substituting the Weibull reliability equation into the likelihood function so that it is in terms of β and time or reliability, as discussed in Chapter 5. The likelihood ratio equation used to solve for bounds on time (Type 1) is:
- [math]\displaystyle{ L(\beta ,t)=\prod_{i=1}^{N}\frac{\beta }{\left( \frac{t}{(-\text{ln}(R))^{ \frac{1}{\beta }}}\right) }\cdot \left( \frac{x_{i}}{\left( \frac{t}{(-\text{ ln}(R))^{\frac{1}{\beta }}}\right) }\right) ^{\beta -1}\cdot \text{exp}\left[ -\left( \frac{x_{i}}{\left( \frac{t}{(-\text{ln}(R))^{\frac{1}{\beta }}} \right) }\right) ^{\beta }\right] }[/math]
The likelihood ratio equation used to solve for bounds on reliability (Type 2) is:
- [math]\displaystyle{ L(\beta ,R)=\prod_{i=1}^{N}\frac{\beta }{\left( \frac{t}{(-\text{ln}(R))^{ \frac{1}{\beta }}}\right) }\cdot \left( \frac{x_{i}}{\left( \frac{t}{(-\text{ ln}(R))^{\frac{1}{\beta }}}\right) }\right) ^{\beta -1}\cdot \text{exp}\left[ -\left( \frac{x_{i}}{\left( \frac{t}{(-\text{ln}(R))^{\frac{1}{\beta }}} \right) }\right) ^{\beta }\right] }[/math]
Bayesian Confidence Bounds
Bounds on Parameters
Bayesian Bounds use non-informative prior distributions for both parameters. From Chapter 5, we know that if the prior distribution of η and β are independent, the posterior joint distribution of η and β can be written as:
- [math]\displaystyle{ f(\eta ,\beta |Data)= \dfrac{L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )}{\int_{0}^{\infty }\int_{0}^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
The marginal distribution of η is:
- [math]\displaystyle{ f(\eta |Data) =\int_{0}^{\infty }f(\eta ,\beta |Data)d\beta = \dfrac{\int_{0}^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\beta }{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
where: [math]\displaystyle{ \varphi (\beta )=\frac{1}{\beta } }[/math] is the non-informative prior of β. [math]\displaystyle{ \varphi (\eta )=\frac{1}{\eta } }[/math] is the non-informative prior of η. Using these non-informative prior distributions, [math]\displaystyle{ f(\eta|Data) }[/math] can be rewritten as:
- [math]\displaystyle{ f(\eta |Data)=\dfrac{\int_{0}^{\infty }L(Data|\eta ,\beta )\frac{1}{\beta } \frac{1}{\eta }d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(Data|\eta ,\beta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } }[/math]
The one-sided upper bounds of η is:
- [math]\displaystyle{ CL=P(\eta \leq \eta _{U})=\int_{0}^{\eta _{U}}f(\eta |Data)d\eta }[/math]
The one-sided lower bounds of η is:
- [math]\displaystyle{ 1-CL=P(\eta \leq \eta _{L})=\int_{0}^{\eta _{L}}f(\eta |Data)d\eta }[/math] The two-sided bounds of η is:
- [math]\displaystyle{ CL=P(\eta _{L}\leq \eta \leq \eta _{U})=\int_{\eta _{L}}^{\eta _{U}}f(\eta |Data)d\eta }[/math] Same method is used to obtain the bounds of β.
Bounds on Time (Type 1)
From Chapter 5, we know that:
- [math]\displaystyle{ CL=\Pr (T\leq T_{U})=\Pr (\eta \leq T_{U}\exp (-\frac{\ln (-\ln R)}{\beta })) }[/math] From the posterior distribution of η, we have:
- [math]\displaystyle{ CL=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T_{U}\exp (-\dfrac{ \ln (-\ln R)}{\beta })}L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } EQNREF BayesCLT }[/math]
Eqn. (EQNREF BayesCLT ) is solved numerically for TU. The same method can be applied to calculate one sided lower bounds and two-sided bounds on time.
Bounds on Reliability (Type 2)
- [math]\displaystyle{ CL=\Pr (R\leq R_{U})=\Pr (\eta \leq T\exp (-\frac{\ln (-\ln R_{U})}{\beta })) }[/math] From the posterior distribution of η, we have:
- [math]\displaystyle{ CL=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T\exp (-\dfrac{\ln (-\ln R_{U})}{\beta })}L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } EQNREF BayesCLR }[/math]
Eqn. (EQNREF BayesCLR ) is solved numerically for RU. The same method can be used to calculate the one sided lower bounds and two-sided bounds on reliability.
Weibull-Bayesian Analysis
In this section, the Bayesian methods are presented for the two-parameter Weibull distribution. Bayesian concepts were introduced in Chapter 3. This model considers prior knowledge on the shape (β) parameter of the Weibull distribution when it is chosen to be fitted to a given set of data. There are many practical applications for this model, particularly when dealing with small sample sizes and some prior knowledge for the shape parameter is available. For example, when a test is performed, there is often a good understanding about the behavior of the failure mode under investigation, primarily through historical data. At the same time, most reliability tests are performed on a limited number of samples. Under these conditions, it would be very useful to use this prior knowledge with the goal of making more accurate predictions. A common approach for such scenarios is to use the one-parameter Weibull distribution, but this approach is too deterministic, too absolute you may say (and you would be right). The Weibull-Bayesian model in Weibull++ (which is actually a true "WeiBayes" model, unlike the one-parameter Weibull that is commonly referred to as such) offers an alternative to the one-parameter Weibull, by including the variation and uncertainty that might have been observed in the past on the shape parameter. Applying Bayes's rule on the two-parameter Weibull distribution and assuming the prior distributions of β and η are independent, we obtain the following posterior :
- [math]\displaystyle{ f(\beta ,\eta |Data)=\dfrac{L(\beta ,\eta )\varphi (\beta )\varphi (\eta )}{ \int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math] EQNREF WeibBayes
In this model, η is assumed to follow a noninformative prior distribution with the density function [math]\displaystyle{ \varphi (\eta )=\dfrac{1}{\eta } }[/math]. This is called Jeffrey's prior, and is obtained by performing a logarithmic transformation on η. Specifically, since η is always positive, we can assume that ln(η) follows a uniform distribution, U( − ∞, + ∞). Applying Jeffrey's rule [9] which says "in general, an approximate non-informative prior is taken proportional to the square root of Fisher's information", yields [math]\displaystyle{ \varphi (\eta )=\dfrac{1}{\eta }. }[/math]
The prior distribution of β, denoted as [math]\displaystyle{ \varphi (\beta ) }[/math], can be selected from the following distributions: normal, lognormal, exponential and uniform. The procedure of performing a Weibull-Bayesian analysis is as follows:
- Collect the times-to-failure data.
- Specify a prior distribution for β (the prior for η is assumed to be 1/η).
- Obtain the posterior from Eqn. (EQNREF WeibBayes ).
In other words, a distribution (the posterior ) is obtained, rather than a point estimate as in classical statistics (i.e., as in the parameter estimation methods described previously in this chapter). Therefore, if a point estimate needs to be reported, a point of the posterior needs to be calculated. Typical points of the posterior distribution used are the mean (expected value) or median. In Weibull++, both options are available and can be chosen from the Analysis page, under the Results As area, as shown next.
The expected value of β is obtained by:
- [math]\displaystyle{ E(\beta )=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\beta \cdot f(\beta ,\eta |Data)d\beta d\eta }[/math]
Similarly, the expected value of η is obtained by:
- [math]\displaystyle{ E(\eta )=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\eta \cdot f(\beta ,\eta |Data)d\beta d\eta }[/math]
The median points are obtained by solving the following equations for [math]\displaystyle{ \breve{\beta} }[/math] and [math]\displaystyle{ \breve{\eta} }[/math] respectively:
- [math]\displaystyle{ \int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\breve{\beta}}f(\beta ,\eta |Data)d\beta d\eta =0.5 }[/math]
- and
- [math]\displaystyle{ \int\nolimits_{0}^{\breve{\eta}}\int\nolimits_{0}^{\infty }f(\beta ,\eta |Data)d\beta d\eta =0.5 }[/math]
Of course, other points of the posterior distribution can be calculated as well. For example, one may want to calculate the 10th percentile of the joint posterior distribution (w.r.t. one of the parameters). The procedure for obtaining other points of the posterior distribution is similar to the one for obtaining the median values, where instead of 0.5 the percentage of interest is given. This procedure actually provides the confidence bounds on the parameters, which in the Bayesian framework are called ‘‘Credible Bounds‘‘. However, since the engineering interpretation is the same, and to avoid confusion, we refer to them as confidence bounds in this reference and in Weibull++.
Posterior Distributions for Functions of Parameters
As explained in Chapter 3, in Bayesian analysis, all the functions of the parameters are distributed. In other words, a posterior distribution is obtained for functions such as reliability and failure rate, instead of point estimate as in classical statistics. Therefore, in order to obtain a point estimate for these functions, a point on the posterior distributions needs to be calculated. Again, the expected value (mean) or median value are used.
[math]\displaystyle{ pdf }[/math] of the Times-to-Failure
The posterior distribution of the failure time is given by:
- [math]\displaystyle{ f(T|Data)=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }f(T,\beta ,\eta )f(\beta ,\eta |Data)d\eta d\beta }[/math] EQNREF WeibBayesPDF
- where:
- [math]\displaystyle{ f(T,\beta ,\eta )=\dfrac{\beta }{\eta }\left( \dfrac{T}{\eta }\right) ^{\beta -1}e^{-\left( \dfrac{T}{\eta }\right) ^{\beta }} }[/math]
For the [math]\displaystyle{ pdf }[/math] of the times-to-failure, only the expected value is calculated and reported in Weibull++.
Reliability
In order to calculate the median value of the reliability function, we first need to obtain posterior of the reliability. Since R(T) is a function of β, the density functions of β and R(T) have the following relationship:
- [math]\displaystyle{ \begin{align} f(R|Data,T)dR = & f(\beta |Data)d\beta)\\ = & (\int\nolimits_{0}^{\infty }f(\beta ,\eta |Data)d{\eta}) d{\beta} \\ =& \dfrac{\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }d\beta \end{align} }[/math] EQNREF Rpdf
The median value of the reliability is obtained by solving the following equation w.r.t. [math]\displaystyle{ \breve{R}: }[/math]
- [math]\displaystyle{ \int\nolimits_{0}^{\breve{R}}f(R|Data,T)dR=0.5 }[/math] EQNREF MedRel
The expected value of the reliability at time is given by:
- [math]\displaystyle{ R(T|Data)=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }R(T,\beta ,\eta )f(\beta ,\eta |Data)d\eta d\beta }[/math] where:
- [math]\displaystyle{ R(T,\beta ,\eta )=e^{-\left( \dfrac{T}{\eta }\right) ^{^{\beta }}} }[/math]
Failure Rate
The failure rate at time is given by:
- [math]\displaystyle{ \lambda (T|Data)=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\lambda (T,\beta ,\eta )L(\beta ,\eta )\varphi (\eta )\varphi (\beta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
- where:
- [math]\displaystyle{ \lambda (T,\beta ,\eta )=\dfrac{\beta }{\eta }\left( \dfrac{T}{\eta }\right) ^{\beta -1} }[/math]
Note on Calculated Results
As mentioned above, in order to obtain point estimates for the parameters of functions of the parameters in Bayesian analysis, the Median or Mean values of the different posterior [math]\displaystyle{ pdf }[/math]s are calculated. It is important to note that the Median value is preferable and is the default in Weibull++. This is because the Median value always corresponds to the 50th percentile of the distribution. On the other hand, the Mean is not a fixed point on the distribution, which could cause issues, especially when comparing results across different data sets.
Confidence Bounds on R(T)
The confidence bounds calculation under the Weibull-Bayesian analysis is very similar to the Bayesian Confidence Bounds method described in the previous section, with the exception that in the case of the Weibull-Bayesian Analysis the specified prior of β is considered instead of an non-informative prior. The Bayesian one-sided upper bound estimate for R(T) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{U}(T)}f(R|Data,T)dR=CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and (EQNREF Rpdf ) the following is obtained:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{T\exp (-\dfrac{\ln (-\ln R_{U})}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLRU
Eqn. (EQNREF 1CLRU ) can be solved for RU(T). The Bayesian one-sided lower bound estimate for [math]\displaystyle{ \ R(T) }[/math] is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{L}(T)}f(R|Data,T)dR=1-CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and (EQNREF Rpdf ) the following is obtained:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T\exp (-\dfrac{\ln (-\ln R_{L})}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=1-CL }[/math] EQNREF 1CLRL
Eqn. (EQNREF 1CLRL ) can be solved for RL(T). The Bayesian two-sided bounds estimate for R(T) is given by:
- [math]\displaystyle{ \int\nolimits_{R_{L}(T)}^{R_{U}(T)}f(R|Data,T)dR=CL }[/math] which is equivalent to:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{U}(T)}f(R|Data,T)dR=(1+CL)/2 }[/math]
- and
- [math]\displaystyle{ \int\nolimits_{0}^{R_{L}(T)}f(R|Data,T)dR=(1-CL)/2 }[/math]
Using the same method for one-sided bounds, RU(T)and RL(T) can be computed.
Confidence Bounds on Time [math]\displaystyle{ T }[/math]
Following the same procedure described for bounds on Reliability, the bounds of time can be calculated, given . The Bayesian one-sided upper bound estimate for T(R) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{U}(R)}f(T|Data,R)dT=CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and. (EQNREF WeibBayesPDF ), we obtain:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T_{U}\exp (-\dfrac{\ln (-\ln R)}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLTU
Eqn. (EQNREF 1CLTU ) can be solved for TU(R). The Bayesian one-sided lower bound estimate for T(R) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{L}(R)}f(T|Data,R)dT=1-CL }[/math]
- or:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{T_{L}\exp (\dfrac{-\ln (-\ln R)}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLTL
Eqn. (EQNREF 1CLTL ) can be solved for TL(R). The Bayesian two-sided lower bounds estimate for T(R) is:
- [math]\displaystyle{ \int\nolimits_{T_{L}(R)}^{T_{U}(R)}f(T|Data,R)dT=CL }[/math]
which is equivalent to:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{U}(R)}f(T|Data,R)dT=(1+CL)/2 }[/math]
- and:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{L}(R)}f(T|Data,R)dT=(1-CL)/2 }[/math]
Example 6
A manufacturer has tested prototypes of a modified product. The test was terminated at 2000 hours, with only two failures observed from a sample size of eighteen.
| Number of State | State of F or S | State End Time |
|---|---|---|
| 1 | F | 1180 |
| 1 | F | 1842 |
| 16 | S | 2000 |
Because of the lack of failure data in the prototype testing, the manufacturer decided to use information gathered from prior tests on this product to increase the confidence in the results of the prototype testing. This decision was made because failure analysis indicated that the failure mode of these two failures is the same as the one observed in previous tests. In other words, it is expected that the shape of the distribution hasn't changed, but hopefully the scale has, indicating longer life. The two-parameter Weibull distribution have been used to model all prior tests results. The list of the estimated β parameter is as follows:
| Betas Obtained for Similar Mode |
|---|
| 1.7 |
| 2.1 |
| 2.4 |
| 3.1 |
| 3.5 |
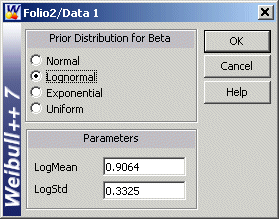
First, in order to fit the data to a Weibull-Bayesian model, a prior distribution for β needs to be determined. Based on the prior tests' β values, the prior distribution for β was found to be a lognormal distribution with μ = 0.9064, σ = 0.3325 (obtained by entering the β values into a Weibull++ Standard Folio and analyzing it based on the RRX analysis method.)
the test data is entered into a Standard Folio, the Weibull-Bayesian is selected under Distribution and the β prior distribution is entered after clicking the Calculate button.
Suppose that the reliability at 3000hr is the metric of interest in this example. This reliability can be obtained using Eqn. (EQNREF MedRel ), resulting in the median value of the posterior of the reliability at 3000hr. Using the QCP, this value is calculated to be 76.97. ( By default Weibull++ returns the median values of the posterior distribution. )
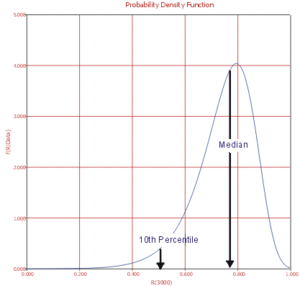
The posterior [math]\displaystyle{ pdf }[/math] of the reliability function at 3000hrs can be obtained using Eqn. (EQNREF Rpdf ). In Figure 6-10 the posterior [math]\displaystyle{ pdf }[/math] of the reliability at 3000hrs is plotted, with the corresponding median value as well as the 10th percentile value shown. The 10th percentile constitutes the 90 Lower 1-Sided bound on the reliability at 3000hrs, which is calculated to be 50.77.
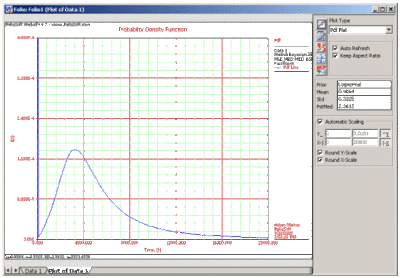
Notice that the [math]\displaystyle{ pdf }[/math] plotted in Fig. 6-10 is of the reliability at 3000hrs, and not the [math]\displaystyle{ pdf }[/math] of the times-to-failure data. The [math]\displaystyle{ pdf }[/math] of the times-to-failure data can be obtained using Eqn. (EQNREF WeibBayesPDF ) and plotted using Weibull++, as shown next:
| The material on this page is copyrighted. | ©1992-2012. ReliaSoft Corporation. ALL RIGHTS RESERVED. |
The Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} \,\! }[/math], (also called MTTF) of the Weibull pdf is given by:
- [math]\displaystyle{ \overline{T}=\gamma +\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
where
- [math]\displaystyle{ \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
is the gamma function evaluated at the value of:
- [math]\displaystyle{ \left( { \frac{1}{\beta }}+1\right) \,\! }[/math]
The gamma function is defined as:
- [math]\displaystyle{ \Gamma (n)=\int_{0}^{\infty }e^{-x}x^{n-1}dx \,\! }[/math]
For the 2-parameter case, this can be reduced to:
- [math]\displaystyle{ \overline{T}=\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
Note that some practitioners erroneously assume that [math]\displaystyle{ \eta \,\! }[/math] is equal to the MTTF, [math]\displaystyle{ \overline{T}\,\! }[/math]. This is only true for the case of: [math]\displaystyle{ \beta=1 \,\! }[/math] or:
- [math]\displaystyle{ \begin{align} \overline{T} &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {2}\right) \\ &= \eta \cdot 1\\ &= \eta \end{align} \,\! }[/math]
The Median
The median, [math]\displaystyle{ \breve{T}\,\! }[/math], of the Weibull distribution is given by:
- [math]\displaystyle{ \breve{T}=\gamma +\eta \left( \ln 2\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Mode
The mode, [math]\displaystyle{ \tilde{T} \,\! }[/math], is given by:
- [math]\displaystyle{ \tilde{T}=\gamma +\eta \left( 1-\frac{1}{\beta }\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Standard Deviation
The standard deviation, [math]\displaystyle{ \sigma _{T}\,\! }[/math], is given by:
- [math]\displaystyle{ \sigma _{T}=\eta \cdot \sqrt{\Gamma \left( {\frac{2}{\beta }}+1\right) -\Gamma \left( {\frac{1}{ \beta }}+1\right) ^{2}} \,\! }[/math]
The Weibull Reliability Function
The equation for the 3-parameter Weibull cumulative density function, cdf, is given by:
- [math]\displaystyle{ F(t)=1-e^{-\left( \frac{t-\gamma }{\eta }\right) ^{\beta }} \,\! }[/math]
This is also referred to as unreliability and designated as [math]\displaystyle{ Q(t) \,\! }[/math] by some authors.
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function for the 3-parameter Weibull distribution is then given by:
- [math]\displaystyle{ R(t)=e^{-\left( { \frac{t-\gamma }{\eta }}\right) ^{\beta }} \,\! }[/math]
The Weibull Conditional Reliability Function
The 3-parameter Weibull conditional reliability function is given by:
- [math]\displaystyle{ R(t|T)={ \frac{R(T+t)}{R(T)}}={\frac{e^{-\left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }}}{e^{-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }}}} \,\! }[/math]
or:
- [math]\displaystyle{ R(t|T)=e^{-\left[ \left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }\right] } \,\! }[/math]
These give the reliability for a new mission of [math]\displaystyle{ t \,\! }[/math] duration, having already accumulated [math]\displaystyle{ T \,\! }[/math] time of operation up to the start of this new mission, and the units are checked out to assure that they will start the next mission successfully. It is called conditional because you can calculate the reliability of a new mission based on the fact that the unit or units already accumulated hours of operation successfully.
The Weibull Reliable Life
The reliable life, [math]\displaystyle{ T_{R}\,\! }[/math], of a unit for a specified reliability, [math]\displaystyle{ R\,\! }[/math], starting the mission at age zero, is given by:
- [math]\displaystyle{ T_{R}=\gamma +\eta \cdot \left\{ -\ln ( R ) \right\} ^{ \frac{1}{\beta }} \,\! }[/math]
This is the life for which the unit/item will be functioning successfully with a reliability of [math]\displaystyle{ R\,\! }[/math]. If [math]\displaystyle{ R = 0.50\,\! }[/math], then [math]\displaystyle{ T_{R}=\breve{T} \,\! }[/math], the median life, or the life by which half of the units will survive.
The Weibull Failure Rate Function
The Weibull failure rate function, [math]\displaystyle{ \lambda(t) \,\! }[/math], is given by:
- [math]\displaystyle{ \lambda \left( t\right) = \frac{f\left( t\right) }{R\left( t\right) }=\frac{\beta }{\eta }\left( \frac{ t-\gamma }{\eta }\right) ^{\beta -1} \,\! }[/math]
The Weibull distribution is widely used in reliability and life data analysis due to its versatility. Depending on the values of the parameters, the Weibull distribution can be used to model a variety of life behaviors. We will now examine how the values of the shape parameter, [math]\displaystyle{ \beta\,\! }[/math], and the scale parameter, [math]\displaystyle{ \eta\,\! }[/math], affect such distribution characteristics as the shape of the curve, the reliability and the failure rate. Note that in the rest of this section we will assume the most general form of the Weibull distribution, (i.e., the 3-parameter form). The appropriate substitutions to obtain the other forms, such as the 2-parameter form where [math]\displaystyle{ \gamma = 0,\,\! }[/math] or the 1-parameter form where [math]\displaystyle{ \beta = C = \,\! }[/math] constant, can easily be made.
Effects of the Shape Parameter, beta
The Weibull shape parameter, [math]\displaystyle{ \beta\,\! }[/math], is also known as the slope. This is because the value of [math]\displaystyle{ \beta\,\! }[/math] is equal to the slope of the regressed line in a probability plot. Different values of the shape parameter can have marked effects on the behavior of the distribution. In fact, some values of the shape parameter will cause the distribution equations to reduce to those of other distributions. For example, when [math]\displaystyle{ \beta = 1\,\! }[/math], the pdf of the 3-parameter Weibull distribution reduces to that of the 2-parameter exponential distribution or:
- [math]\displaystyle{ f(t)={\frac{1}{\eta }}e^{-{\frac{t-\gamma }{\eta }}} \,\! }[/math]
where [math]\displaystyle{ \frac{1}{\eta }=\lambda = \,\! }[/math] failure rate. The parameter [math]\displaystyle{ \beta\,\! }[/math] is a pure number, (i.e., it is dimensionless). The following figure shows the effect of different values of the shape parameter, [math]\displaystyle{ \beta\,\! }[/math], on the shape of the pdf. As you can see, the shape can take on a variety of forms based on the value of [math]\displaystyle{ \beta\,\! }[/math].
For [math]\displaystyle{ 0\lt \beta \leq 1 \,\! }[/math]:
- As [math]\displaystyle{ t \rightarrow 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\! }[/math]), [math]\displaystyle{ f(t)\rightarrow \infty.\,\! }[/math]
- As [math]\displaystyle{ t\rightarrow \infty\,\! }[/math], [math]\displaystyle{ f(t)\rightarrow 0\,\! }[/math].
- [math]\displaystyle{ f(t)\,\! }[/math] decreases monotonically and is convex as it increases beyond the value of [math]\displaystyle{ \gamma\,\! }[/math].
- The mode is non-existent.
For [math]\displaystyle{ \beta \gt 1 \,\! }[/math]:
- [math]\displaystyle{ f(t) = 0\,\! }[/math] at [math]\displaystyle{ t = 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\! }[/math]).
- [math]\displaystyle{ f(t)\,\! }[/math] increases as [math]\displaystyle{ t\rightarrow \tilde{T} \,\! }[/math] (the mode) and decreases thereafter.
- For [math]\displaystyle{ \beta \lt 2.6\,\! }[/math] the Weibull pdf is positively skewed (has a right tail), for [math]\displaystyle{ 2.6 \lt \beta \lt 3.7\,\! }[/math] its coefficient of skewness approaches zero (no tail). Consequently, it may approximate the normal pdf, and for [math]\displaystyle{ \beta \gt 3.7\,\! }[/math] it is negatively skewed (left tail). The way the value of [math]\displaystyle{ \beta\,\! }[/math] relates to the physical behavior of the items being modeled becomes more apparent when we observe how its different values affect the reliability and failure rate functions. Note that for [math]\displaystyle{ \beta = 0.999\,\! }[/math], [math]\displaystyle{ f(0) = \infty\,\! }[/math], but for [math]\displaystyle{ \beta = 1.001\,\! }[/math], [math]\displaystyle{ f(0) = 0.\,\! }[/math] This abrupt shift is what complicates MLE estimation when [math]\displaystyle{ \beta\,\! }[/math] is close to 1.
The Effect of beta on the cdf and Reliability Function
The above figure shows the effect of the value of [math]\displaystyle{ \beta\,\! }[/math] on the cdf, as manifested in the Weibull probability plot. It is easy to see why this parameter is sometimes referred to as the slope. Note that the models represented by the three lines all have the same value of [math]\displaystyle{ \eta\,\! }[/math]. The following figure shows the effects of these varied values of [math]\displaystyle{ \beta\,\! }[/math] on the reliability plot, which is a linear analog of the probability plot.
- [math]\displaystyle{ R(t)\,\! }[/math] decreases sharply and monotonically for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] and is convex.
- For [math]\displaystyle{ \beta = 1\,\! }[/math], [math]\displaystyle{ R(t)\,\! }[/math] decreases monotonically but less sharply than for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] and is convex.
- For [math]\displaystyle{ \beta \gt 1\,\! }[/math], [math]\displaystyle{ R(t)\,\! }[/math] decreases as increases. As wear-out sets in, the curve goes through an inflection point and decreases sharply.
The Effect of beta on the Weibull Failure Rate
The value of [math]\displaystyle{ \beta\,\! }[/math] has a marked effect on the failure rate of the Weibull distribution and inferences can be drawn about a population's failure characteristics just by considering whether the value of [math]\displaystyle{ \beta\,\! }[/math] is less than, equal to, or greater than one.
As indicated by above figure, populations with [math]\displaystyle{ \beta \lt 1\,\! }[/math] exhibit a failure rate that decreases with time, populations with [math]\displaystyle{ \beta = 1\,\! }[/math] have a constant failure rate (consistent with the exponential distribution) and populations with [math]\displaystyle{ \beta \gt 1\,\! }[/math] have a failure rate that increases with time. All three life stages of the bathtub curve can be modeled with the Weibull distribution and varying values of [math]\displaystyle{ \beta\,\! }[/math]. The Weibull failure rate for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] is unbounded at [math]\displaystyle{ T = 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\!)\,\! }[/math]. The failure rate, [math]\displaystyle{ \lambda(t),\,\! }[/math] decreases thereafter monotonically and is convex, approaching the value of zero as [math]\displaystyle{ t\rightarrow \infty\,\! }[/math] or [math]\displaystyle{ \lambda (\infty) = 0\,\! }[/math]. This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When encountering such behavior in a manufactured product, it may be indicative of problems in the production process, inadequate burn-in, substandard parts and components, or problems with packaging and shipping. For [math]\displaystyle{ \beta = 1\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] yields a constant value of [math]\displaystyle{ { \frac{1}{\eta }} \,\! }[/math] or:
- [math]\displaystyle{ \lambda (t)=\lambda ={\frac{1}{\eta }} \,\! }[/math]
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
For [math]\displaystyle{ \beta \gt 1\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] increases as [math]\displaystyle{ t\,\! }[/math] increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For [math]\displaystyle{ 1 \lt \beta \lt 2,\,\! }[/math] the [math]\displaystyle{ \lambda(t)\,\! }[/math] curve is concave, consequently the failure rate increases at a decreasing rate as [math]\displaystyle{ t\,\! }[/math] increases.
For [math]\displaystyle{ \beta = 2\,\! }[/math] there emerges a straight line relationship between [math]\displaystyle{ \lambda(t)\,\! }[/math] and [math]\displaystyle{ t\,\! }[/math], starting at a value of [math]\displaystyle{ \lambda(t) = 0\,\! }[/math] at [math]\displaystyle{ t = \gamma\,\! }[/math], and increasing thereafter with a slope of [math]\displaystyle{ { \frac{2}{\eta ^{2}}} \,\! }[/math]. Consequently, the failure rate increases at a constant rate as [math]\displaystyle{ t\,\! }[/math] increases. Furthermore, if [math]\displaystyle{ \eta = 1\,\! }[/math] the slope becomes equal to 2, and when [math]\displaystyle{ \gamma = 0\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] becomes a straight line which passes through the origin with a slope of 2. Note that at [math]\displaystyle{ \beta = 2\,\! }[/math], the Weibull distribution equations reduce to that of the Rayleigh distribution.
When [math]\displaystyle{ \beta \gt 2,\,\! }[/math] the [math]\displaystyle{ \lambda(t)\,\! }[/math] curve is convex, with its slope increasing as [math]\displaystyle{ t\,\! }[/math] increases. Consequently, the failure rate increases at an increasing rate as [math]\displaystyle{ t\,\! }[/math] increases, indicating wearout life.
Effects of the Scale Parameter, eta
A change in the scale parameter [math]\displaystyle{ \eta\,\! }[/math] has the same effect on the distribution as a change of the abscissa scale. Increasing the value of [math]\displaystyle{ \eta\,\! }[/math] while holding [math]\displaystyle{ \beta\,\! }[/math] constant has the effect of stretching out the pdf. Since the area under a pdf curve is a constant value of one, the "peak" of the pdf curve will also decrease with the increase of [math]\displaystyle{ \eta\,\! }[/math], as indicated in the above figure.
- If [math]\displaystyle{ \eta\,\! }[/math] is increased while [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math] are kept the same, the distribution gets stretched out to the right and its height decreases, while maintaining its shape and location.
- If [math]\displaystyle{ \eta\,\! }[/math] is decreased while [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math] are kept the same, the distribution gets pushed in towards the left (i.e., towards its beginning or towards 0 or [math]\displaystyle{ \gamma\,\! }[/math]), and its height increases.
- [math]\displaystyle{ \eta\,\! }[/math] has the same units as [math]\displaystyle{ t\,\! }[/math], such as hours, miles, cycles, actuations, etc.
Effects of the Location Parameter, gamma
The location parameter, [math]\displaystyle{ \gamma\,\! }[/math], as the name implies, locates the distribution along the abscissa. Changing the value of [math]\displaystyle{ \gamma\,\! }[/math] has the effect of sliding the distribution and its associated function either to the right (if [math]\displaystyle{ \gamma \gt 0\,\! }[/math]) or to the left (if [math]\displaystyle{ \gamma \lt 0\,\! }[/math]).
- When [math]\displaystyle{ \gamma = 0,\,\! }[/math] the distribution starts at [math]\displaystyle{ t=0\,\! }[/math] or at the origin.
- If [math]\displaystyle{ \gamma \gt 0,\,\! }[/math] the distribution starts at the location [math]\displaystyle{ \gamma\,\! }[/math] to the right of the origin.
- If [math]\displaystyle{ \gamma \lt 0,\,\! }[/math] the distribution starts at the location [math]\displaystyle{ \gamma\,\! }[/math] to the left of the origin.
- [math]\displaystyle{ \gamma\,\! }[/math] provides an estimate of the earliest time-to-failure of such units.
- The life period 0 to [math]\displaystyle{ + \gamma\,\! }[/math] is a failure free operating period of such units.
- The parameter [math]\displaystyle{ \gamma\,\! }[/math] may assume all values and provides an estimate of the earliest time a failure may be observed. A negative [math]\displaystyle{ \gamma\,\! }[/math] may indicate that failures have occurred prior to the beginning of the test, namely during production, in storage, in transit, during checkout prior to the start of a mission, or prior to actual use.
- [math]\displaystyle{ \gamma\,\! }[/math] has the same units as [math]\displaystyle{ t\,\! }[/math], such as hours, miles, cycles, actuations, etc.
The Weibull Distribution
The Weibull distribution is one of the most widely used lifetime distributions in reliability engineering. It is a versatile distribution that can take on the characteristics of other types of distributions, based on the value of the shape parameter, [math]\displaystyle{ \boldsymbol{\beta} }[/math]. This chapter provides a brief background on the Weibull distribution, presents and derives most of the applicable equations and presents examples calculated both manually and by using ReliaSoft's Weibull++.
Template loop detected: Template:Weibull Probability Density Function
The Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} \,\! }[/math], (also called MTTF) of the Weibull pdf is given by:
- [math]\displaystyle{ \overline{T}=\gamma +\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
where
- [math]\displaystyle{ \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
is the gamma function evaluated at the value of:
- [math]\displaystyle{ \left( { \frac{1}{\beta }}+1\right) \,\! }[/math]
The gamma function is defined as:
- [math]\displaystyle{ \Gamma (n)=\int_{0}^{\infty }e^{-x}x^{n-1}dx \,\! }[/math]
For the 2-parameter case, this can be reduced to:
- [math]\displaystyle{ \overline{T}=\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
Note that some practitioners erroneously assume that [math]\displaystyle{ \eta \,\! }[/math] is equal to the MTTF, [math]\displaystyle{ \overline{T}\,\! }[/math]. This is only true for the case of: [math]\displaystyle{ \beta=1 \,\! }[/math] or:
- [math]\displaystyle{ \begin{align} \overline{T} &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {2}\right) \\ &= \eta \cdot 1\\ &= \eta \end{align} \,\! }[/math]
The Median
The median, [math]\displaystyle{ \breve{T}\,\! }[/math], of the Weibull distribution is given by:
- [math]\displaystyle{ \breve{T}=\gamma +\eta \left( \ln 2\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Mode
The mode, [math]\displaystyle{ \tilde{T} \,\! }[/math], is given by:
- [math]\displaystyle{ \tilde{T}=\gamma +\eta \left( 1-\frac{1}{\beta }\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Standard Deviation
The standard deviation, [math]\displaystyle{ \sigma _{T}\,\! }[/math], is given by:
- [math]\displaystyle{ \sigma _{T}=\eta \cdot \sqrt{\Gamma \left( {\frac{2}{\beta }}+1\right) -\Gamma \left( {\frac{1}{ \beta }}+1\right) ^{2}} \,\! }[/math]
The Weibull Reliability Function
The equation for the 3-parameter Weibull cumulative density function, cdf, is given by:
- [math]\displaystyle{ F(t)=1-e^{-\left( \frac{t-\gamma }{\eta }\right) ^{\beta }} \,\! }[/math]
This is also referred to as unreliability and designated as [math]\displaystyle{ Q(t) \,\! }[/math] by some authors.
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function for the 3-parameter Weibull distribution is then given by:
- [math]\displaystyle{ R(t)=e^{-\left( { \frac{t-\gamma }{\eta }}\right) ^{\beta }} \,\! }[/math]
The Weibull Conditional Reliability Function
The 3-parameter Weibull conditional reliability function is given by:
- [math]\displaystyle{ R(t|T)={ \frac{R(T+t)}{R(T)}}={\frac{e^{-\left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }}}{e^{-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }}}} \,\! }[/math]
or:
- [math]\displaystyle{ R(t|T)=e^{-\left[ \left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }\right] } \,\! }[/math]
These give the reliability for a new mission of [math]\displaystyle{ t \,\! }[/math] duration, having already accumulated [math]\displaystyle{ T \,\! }[/math] time of operation up to the start of this new mission, and the units are checked out to assure that they will start the next mission successfully. It is called conditional because you can calculate the reliability of a new mission based on the fact that the unit or units already accumulated hours of operation successfully.
The Weibull Reliable Life
The reliable life, [math]\displaystyle{ T_{R}\,\! }[/math], of a unit for a specified reliability, [math]\displaystyle{ R\,\! }[/math], starting the mission at age zero, is given by:
- [math]\displaystyle{ T_{R}=\gamma +\eta \cdot \left\{ -\ln ( R ) \right\} ^{ \frac{1}{\beta }} \,\! }[/math]
This is the life for which the unit/item will be functioning successfully with a reliability of [math]\displaystyle{ R\,\! }[/math]. If [math]\displaystyle{ R = 0.50\,\! }[/math], then [math]\displaystyle{ T_{R}=\breve{T} \,\! }[/math], the median life, or the life by which half of the units will survive.
The Weibull Failure Rate Function
The Weibull failure rate function, [math]\displaystyle{ \lambda(t) \,\! }[/math], is given by:
- [math]\displaystyle{ \lambda \left( t\right) = \frac{f\left( t\right) }{R\left( t\right) }=\frac{\beta }{\eta }\left( \frac{ t-\gamma }{\eta }\right) ^{\beta -1} \,\! }[/math]
The Weibull distribution is widely used in reliability and life data analysis due to its versatility. Depending on the values of the parameters, the Weibull distribution can be used to model a variety of life behaviors. We will now examine how the values of the shape parameter, [math]\displaystyle{ \beta\,\! }[/math], and the scale parameter, [math]\displaystyle{ \eta\,\! }[/math], affect such distribution characteristics as the shape of the curve, the reliability and the failure rate. Note that in the rest of this section we will assume the most general form of the Weibull distribution, (i.e., the 3-parameter form). The appropriate substitutions to obtain the other forms, such as the 2-parameter form where [math]\displaystyle{ \gamma = 0,\,\! }[/math] or the 1-parameter form where [math]\displaystyle{ \beta = C = \,\! }[/math] constant, can easily be made.
Effects of the Shape Parameter, beta
The Weibull shape parameter, [math]\displaystyle{ \beta\,\! }[/math], is also known as the slope. This is because the value of [math]\displaystyle{ \beta\,\! }[/math] is equal to the slope of the regressed line in a probability plot. Different values of the shape parameter can have marked effects on the behavior of the distribution. In fact, some values of the shape parameter will cause the distribution equations to reduce to those of other distributions. For example, when [math]\displaystyle{ \beta = 1\,\! }[/math], the pdf of the 3-parameter Weibull distribution reduces to that of the 2-parameter exponential distribution or:
- [math]\displaystyle{ f(t)={\frac{1}{\eta }}e^{-{\frac{t-\gamma }{\eta }}} \,\! }[/math]
where [math]\displaystyle{ \frac{1}{\eta }=\lambda = \,\! }[/math] failure rate. The parameter [math]\displaystyle{ \beta\,\! }[/math] is a pure number, (i.e., it is dimensionless). The following figure shows the effect of different values of the shape parameter, [math]\displaystyle{ \beta\,\! }[/math], on the shape of the pdf. As you can see, the shape can take on a variety of forms based on the value of [math]\displaystyle{ \beta\,\! }[/math].
For [math]\displaystyle{ 0\lt \beta \leq 1 \,\! }[/math]:
- As [math]\displaystyle{ t \rightarrow 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\! }[/math]), [math]\displaystyle{ f(t)\rightarrow \infty.\,\! }[/math]
- As [math]\displaystyle{ t\rightarrow \infty\,\! }[/math], [math]\displaystyle{ f(t)\rightarrow 0\,\! }[/math].
- [math]\displaystyle{ f(t)\,\! }[/math] decreases monotonically and is convex as it increases beyond the value of [math]\displaystyle{ \gamma\,\! }[/math].
- The mode is non-existent.
For [math]\displaystyle{ \beta \gt 1 \,\! }[/math]:
- [math]\displaystyle{ f(t) = 0\,\! }[/math] at [math]\displaystyle{ t = 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\! }[/math]).
- [math]\displaystyle{ f(t)\,\! }[/math] increases as [math]\displaystyle{ t\rightarrow \tilde{T} \,\! }[/math] (the mode) and decreases thereafter.
- For [math]\displaystyle{ \beta \lt 2.6\,\! }[/math] the Weibull pdf is positively skewed (has a right tail), for [math]\displaystyle{ 2.6 \lt \beta \lt 3.7\,\! }[/math] its coefficient of skewness approaches zero (no tail). Consequently, it may approximate the normal pdf, and for [math]\displaystyle{ \beta \gt 3.7\,\! }[/math] it is negatively skewed (left tail). The way the value of [math]\displaystyle{ \beta\,\! }[/math] relates to the physical behavior of the items being modeled becomes more apparent when we observe how its different values affect the reliability and failure rate functions. Note that for [math]\displaystyle{ \beta = 0.999\,\! }[/math], [math]\displaystyle{ f(0) = \infty\,\! }[/math], but for [math]\displaystyle{ \beta = 1.001\,\! }[/math], [math]\displaystyle{ f(0) = 0.\,\! }[/math] This abrupt shift is what complicates MLE estimation when [math]\displaystyle{ \beta\,\! }[/math] is close to 1.
The Effect of beta on the cdf and Reliability Function
The above figure shows the effect of the value of [math]\displaystyle{ \beta\,\! }[/math] on the cdf, as manifested in the Weibull probability plot. It is easy to see why this parameter is sometimes referred to as the slope. Note that the models represented by the three lines all have the same value of [math]\displaystyle{ \eta\,\! }[/math]. The following figure shows the effects of these varied values of [math]\displaystyle{ \beta\,\! }[/math] on the reliability plot, which is a linear analog of the probability plot.
- [math]\displaystyle{ R(t)\,\! }[/math] decreases sharply and monotonically for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] and is convex.
- For [math]\displaystyle{ \beta = 1\,\! }[/math], [math]\displaystyle{ R(t)\,\! }[/math] decreases monotonically but less sharply than for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] and is convex.
- For [math]\displaystyle{ \beta \gt 1\,\! }[/math], [math]\displaystyle{ R(t)\,\! }[/math] decreases as increases. As wear-out sets in, the curve goes through an inflection point and decreases sharply.
The Effect of beta on the Weibull Failure Rate
The value of [math]\displaystyle{ \beta\,\! }[/math] has a marked effect on the failure rate of the Weibull distribution and inferences can be drawn about a population's failure characteristics just by considering whether the value of [math]\displaystyle{ \beta\,\! }[/math] is less than, equal to, or greater than one.
As indicated by above figure, populations with [math]\displaystyle{ \beta \lt 1\,\! }[/math] exhibit a failure rate that decreases with time, populations with [math]\displaystyle{ \beta = 1\,\! }[/math] have a constant failure rate (consistent with the exponential distribution) and populations with [math]\displaystyle{ \beta \gt 1\,\! }[/math] have a failure rate that increases with time. All three life stages of the bathtub curve can be modeled with the Weibull distribution and varying values of [math]\displaystyle{ \beta\,\! }[/math]. The Weibull failure rate for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] is unbounded at [math]\displaystyle{ T = 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\!)\,\! }[/math]. The failure rate, [math]\displaystyle{ \lambda(t),\,\! }[/math] decreases thereafter monotonically and is convex, approaching the value of zero as [math]\displaystyle{ t\rightarrow \infty\,\! }[/math] or [math]\displaystyle{ \lambda (\infty) = 0\,\! }[/math]. This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When encountering such behavior in a manufactured product, it may be indicative of problems in the production process, inadequate burn-in, substandard parts and components, or problems with packaging and shipping. For [math]\displaystyle{ \beta = 1\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] yields a constant value of [math]\displaystyle{ { \frac{1}{\eta }} \,\! }[/math] or:
- [math]\displaystyle{ \lambda (t)=\lambda ={\frac{1}{\eta }} \,\! }[/math]
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
For [math]\displaystyle{ \beta \gt 1\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] increases as [math]\displaystyle{ t\,\! }[/math] increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For [math]\displaystyle{ 1 \lt \beta \lt 2,\,\! }[/math] the [math]\displaystyle{ \lambda(t)\,\! }[/math] curve is concave, consequently the failure rate increases at a decreasing rate as [math]\displaystyle{ t\,\! }[/math] increases.
For [math]\displaystyle{ \beta = 2\,\! }[/math] there emerges a straight line relationship between [math]\displaystyle{ \lambda(t)\,\! }[/math] and [math]\displaystyle{ t\,\! }[/math], starting at a value of [math]\displaystyle{ \lambda(t) = 0\,\! }[/math] at [math]\displaystyle{ t = \gamma\,\! }[/math], and increasing thereafter with a slope of [math]\displaystyle{ { \frac{2}{\eta ^{2}}} \,\! }[/math]. Consequently, the failure rate increases at a constant rate as [math]\displaystyle{ t\,\! }[/math] increases. Furthermore, if [math]\displaystyle{ \eta = 1\,\! }[/math] the slope becomes equal to 2, and when [math]\displaystyle{ \gamma = 0\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] becomes a straight line which passes through the origin with a slope of 2. Note that at [math]\displaystyle{ \beta = 2\,\! }[/math], the Weibull distribution equations reduce to that of the Rayleigh distribution.
When [math]\displaystyle{ \beta \gt 2,\,\! }[/math] the [math]\displaystyle{ \lambda(t)\,\! }[/math] curve is convex, with its slope increasing as [math]\displaystyle{ t\,\! }[/math] increases. Consequently, the failure rate increases at an increasing rate as [math]\displaystyle{ t\,\! }[/math] increases, indicating wearout life.
Effects of the Scale Parameter, eta
A change in the scale parameter [math]\displaystyle{ \eta\,\! }[/math] has the same effect on the distribution as a change of the abscissa scale. Increasing the value of [math]\displaystyle{ \eta\,\! }[/math] while holding [math]\displaystyle{ \beta\,\! }[/math] constant has the effect of stretching out the pdf. Since the area under a pdf curve is a constant value of one, the "peak" of the pdf curve will also decrease with the increase of [math]\displaystyle{ \eta\,\! }[/math], as indicated in the above figure.
- If [math]\displaystyle{ \eta\,\! }[/math] is increased while [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math] are kept the same, the distribution gets stretched out to the right and its height decreases, while maintaining its shape and location.
- If [math]\displaystyle{ \eta\,\! }[/math] is decreased while [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math] are kept the same, the distribution gets pushed in towards the left (i.e., towards its beginning or towards 0 or [math]\displaystyle{ \gamma\,\! }[/math]), and its height increases.
- [math]\displaystyle{ \eta\,\! }[/math] has the same units as [math]\displaystyle{ t\,\! }[/math], such as hours, miles, cycles, actuations, etc.
Effects of the Location Parameter, gamma
The location parameter, [math]\displaystyle{ \gamma\,\! }[/math], as the name implies, locates the distribution along the abscissa. Changing the value of [math]\displaystyle{ \gamma\,\! }[/math] has the effect of sliding the distribution and its associated function either to the right (if [math]\displaystyle{ \gamma \gt 0\,\! }[/math]) or to the left (if [math]\displaystyle{ \gamma \lt 0\,\! }[/math]).
- When [math]\displaystyle{ \gamma = 0,\,\! }[/math] the distribution starts at [math]\displaystyle{ t=0\,\! }[/math] or at the origin.
- If [math]\displaystyle{ \gamma \gt 0,\,\! }[/math] the distribution starts at the location [math]\displaystyle{ \gamma\,\! }[/math] to the right of the origin.
- If [math]\displaystyle{ \gamma \lt 0,\,\! }[/math] the distribution starts at the location [math]\displaystyle{ \gamma\,\! }[/math] to the left of the origin.
- [math]\displaystyle{ \gamma\,\! }[/math] provides an estimate of the earliest time-to-failure of such units.
- The life period 0 to [math]\displaystyle{ + \gamma\,\! }[/math] is a failure free operating period of such units.
- The parameter [math]\displaystyle{ \gamma\,\! }[/math] may assume all values and provides an estimate of the earliest time a failure may be observed. A negative [math]\displaystyle{ \gamma\,\! }[/math] may indicate that failures have occurred prior to the beginning of the test, namely during production, in storage, in transit, during checkout prior to the start of a mission, or prior to actual use.
- [math]\displaystyle{ \gamma\,\! }[/math] has the same units as [math]\displaystyle{ t\,\! }[/math], such as hours, miles, cycles, actuations, etc.
Template loop detected: Template:Estimation of the Weibull Parameters
Template loop detected: Template:Weibull fisher matrix confidence bounds
Likelihood Ratio Confidence Bounds
As covered in Chapter 5, the likelihood confidence bounds are calculated by finding values for θ1 and θ2 that satisfy:
- [math]\displaystyle{ -2\cdot \text{ln}\left( \frac{L(\theta _{1},\theta _{2})}{L(\hat{\theta }_{1}, \hat{\theta }_{2})}\right) =\chi _{\alpha ;1}^{2} EQNREF lratio2 }[/math]
This equation can be rewritten as:
- [math]\displaystyle{ L(\theta _{1},\theta _{2})=L(\hat{\theta }_{1},\hat{\theta } _{2})\cdot e^{\frac{-\chi _{\alpha ;1}^{2}}{2}} EQNREF lratio3 }[/math]
For complete data, the likelihood function for the Weibull distribution is given by:
- [math]\displaystyle{ L(\beta ,\eta )=\prod_{i=1}^{N}f(x_{i};\beta ,\eta )=\prod_{i=1}^{N}\frac{ \beta }{\eta }\cdot \left( \frac{x_{i}}{\eta }\right) ^{\beta -1}\cdot e^{-\left( \frac{x_{i}}{\eta }\right) ^{\beta }} }[/math]
For a given value of α, values for β and η can be found which represent the maximum and minimum values that satisfy Eqn. (\ref {lratio3}). These represent the confidence bounds for the parameters at a confidence level δ, where α = δ for two-sided bounds and α = 2δ − 1 for one-sided.
Similarly, the bounds on time and reliability can be found by substituting the Weibull reliability equation into the likelihood function so that it is in terms of β and time or reliability, as discussed in Chapter 5. The likelihood ratio equation used to solve for bounds on time (Type 1) is:
- [math]\displaystyle{ L(\beta ,t)=\prod_{i=1}^{N}\frac{\beta }{\left( \frac{t}{(-\text{ln}(R))^{ \frac{1}{\beta }}}\right) }\cdot \left( \frac{x_{i}}{\left( \frac{t}{(-\text{ ln}(R))^{\frac{1}{\beta }}}\right) }\right) ^{\beta -1}\cdot \text{exp}\left[ -\left( \frac{x_{i}}{\left( \frac{t}{(-\text{ln}(R))^{\frac{1}{\beta }}} \right) }\right) ^{\beta }\right] }[/math]
The likelihood ratio equation used to solve for bounds on reliability (Type 2) is:
- [math]\displaystyle{ L(\beta ,R)=\prod_{i=1}^{N}\frac{\beta }{\left( \frac{t}{(-\text{ln}(R))^{ \frac{1}{\beta }}}\right) }\cdot \left( \frac{x_{i}}{\left( \frac{t}{(-\text{ ln}(R))^{\frac{1}{\beta }}}\right) }\right) ^{\beta -1}\cdot \text{exp}\left[ -\left( \frac{x_{i}}{\left( \frac{t}{(-\text{ln}(R))^{\frac{1}{\beta }}} \right) }\right) ^{\beta }\right] }[/math]
Bayesian Confidence Bounds
Bounds on Parameters
Bayesian Bounds use non-informative prior distributions for both parameters. From Chapter 5, we know that if the prior distribution of η and β are independent, the posterior joint distribution of η and β can be written as:
- [math]\displaystyle{ f(\eta ,\beta |Data)= \dfrac{L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )}{\int_{0}^{\infty }\int_{0}^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
The marginal distribution of η is:
- [math]\displaystyle{ f(\eta |Data) =\int_{0}^{\infty }f(\eta ,\beta |Data)d\beta = \dfrac{\int_{0}^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\beta }{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
where: [math]\displaystyle{ \varphi (\beta )=\frac{1}{\beta } }[/math] is the non-informative prior of β. [math]\displaystyle{ \varphi (\eta )=\frac{1}{\eta } }[/math] is the non-informative prior of η. Using these non-informative prior distributions, [math]\displaystyle{ f(\eta|Data) }[/math] can be rewritten as:
- [math]\displaystyle{ f(\eta |Data)=\dfrac{\int_{0}^{\infty }L(Data|\eta ,\beta )\frac{1}{\beta } \frac{1}{\eta }d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(Data|\eta ,\beta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } }[/math]
The one-sided upper bounds of η is:
- [math]\displaystyle{ CL=P(\eta \leq \eta _{U})=\int_{0}^{\eta _{U}}f(\eta |Data)d\eta }[/math]
The one-sided lower bounds of η is:
- [math]\displaystyle{ 1-CL=P(\eta \leq \eta _{L})=\int_{0}^{\eta _{L}}f(\eta |Data)d\eta }[/math] The two-sided bounds of η is:
- [math]\displaystyle{ CL=P(\eta _{L}\leq \eta \leq \eta _{U})=\int_{\eta _{L}}^{\eta _{U}}f(\eta |Data)d\eta }[/math] Same method is used to obtain the bounds of β.
Bounds on Time (Type 1)
From Chapter 5, we know that:
- [math]\displaystyle{ CL=\Pr (T\leq T_{U})=\Pr (\eta \leq T_{U}\exp (-\frac{\ln (-\ln R)}{\beta })) }[/math] From the posterior distribution of η, we have:
- [math]\displaystyle{ CL=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T_{U}\exp (-\dfrac{ \ln (-\ln R)}{\beta })}L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } EQNREF BayesCLT }[/math]
Eqn. (EQNREF BayesCLT ) is solved numerically for TU. The same method can be applied to calculate one sided lower bounds and two-sided bounds on time.
Bounds on Reliability (Type 2)
- [math]\displaystyle{ CL=\Pr (R\leq R_{U})=\Pr (\eta \leq T\exp (-\frac{\ln (-\ln R_{U})}{\beta })) }[/math] From the posterior distribution of η, we have:
- [math]\displaystyle{ CL=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T\exp (-\dfrac{\ln (-\ln R_{U})}{\beta })}L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } EQNREF BayesCLR }[/math]
Eqn. (EQNREF BayesCLR ) is solved numerically for RU. The same method can be used to calculate the one sided lower bounds and two-sided bounds on reliability.
Weibull-Bayesian Analysis
In this section, the Bayesian methods are presented for the two-parameter Weibull distribution. Bayesian concepts were introduced in Chapter 3. This model considers prior knowledge on the shape (β) parameter of the Weibull distribution when it is chosen to be fitted to a given set of data. There are many practical applications for this model, particularly when dealing with small sample sizes and some prior knowledge for the shape parameter is available. For example, when a test is performed, there is often a good understanding about the behavior of the failure mode under investigation, primarily through historical data. At the same time, most reliability tests are performed on a limited number of samples. Under these conditions, it would be very useful to use this prior knowledge with the goal of making more accurate predictions. A common approach for such scenarios is to use the one-parameter Weibull distribution, but this approach is too deterministic, too absolute you may say (and you would be right). The Weibull-Bayesian model in Weibull++ (which is actually a true "WeiBayes" model, unlike the one-parameter Weibull that is commonly referred to as such) offers an alternative to the one-parameter Weibull, by including the variation and uncertainty that might have been observed in the past on the shape parameter. Applying Bayes's rule on the two-parameter Weibull distribution and assuming the prior distributions of β and η are independent, we obtain the following posterior :
- [math]\displaystyle{ f(\beta ,\eta |Data)=\dfrac{L(\beta ,\eta )\varphi (\beta )\varphi (\eta )}{ \int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math] EQNREF WeibBayes
In this model, η is assumed to follow a noninformative prior distribution with the density function [math]\displaystyle{ \varphi (\eta )=\dfrac{1}{\eta } }[/math]. This is called Jeffrey's prior, and is obtained by performing a logarithmic transformation on η. Specifically, since η is always positive, we can assume that ln(η) follows a uniform distribution, U( − ∞, + ∞). Applying Jeffrey's rule [9] which says "in general, an approximate non-informative prior is taken proportional to the square root of Fisher's information", yields [math]\displaystyle{ \varphi (\eta )=\dfrac{1}{\eta }. }[/math]
The prior distribution of β, denoted as [math]\displaystyle{ \varphi (\beta ) }[/math], can be selected from the following distributions: normal, lognormal, exponential and uniform. The procedure of performing a Weibull-Bayesian analysis is as follows:
- Collect the times-to-failure data.
- Specify a prior distribution for β (the prior for η is assumed to be 1/η).
- Obtain the posterior from Eqn. (EQNREF WeibBayes ).
In other words, a distribution (the posterior ) is obtained, rather than a point estimate as in classical statistics (i.e., as in the parameter estimation methods described previously in this chapter). Therefore, if a point estimate needs to be reported, a point of the posterior needs to be calculated. Typical points of the posterior distribution used are the mean (expected value) or median. In Weibull++, both options are available and can be chosen from the Analysis page, under the Results As area, as shown next.
The expected value of β is obtained by:
- [math]\displaystyle{ E(\beta )=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\beta \cdot f(\beta ,\eta |Data)d\beta d\eta }[/math]
Similarly, the expected value of η is obtained by:
- [math]\displaystyle{ E(\eta )=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\eta \cdot f(\beta ,\eta |Data)d\beta d\eta }[/math]
The median points are obtained by solving the following equations for [math]\displaystyle{ \breve{\beta} }[/math] and [math]\displaystyle{ \breve{\eta} }[/math] respectively:
- [math]\displaystyle{ \int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\breve{\beta}}f(\beta ,\eta |Data)d\beta d\eta =0.5 }[/math]
- and
- [math]\displaystyle{ \int\nolimits_{0}^{\breve{\eta}}\int\nolimits_{0}^{\infty }f(\beta ,\eta |Data)d\beta d\eta =0.5 }[/math]
Of course, other points of the posterior distribution can be calculated as well. For example, one may want to calculate the 10th percentile of the joint posterior distribution (w.r.t. one of the parameters). The procedure for obtaining other points of the posterior distribution is similar to the one for obtaining the median values, where instead of 0.5 the percentage of interest is given. This procedure actually provides the confidence bounds on the parameters, which in the Bayesian framework are called ‘‘Credible Bounds‘‘. However, since the engineering interpretation is the same, and to avoid confusion, we refer to them as confidence bounds in this reference and in Weibull++.
Posterior Distributions for Functions of Parameters
As explained in Chapter 3, in Bayesian analysis, all the functions of the parameters are distributed. In other words, a posterior distribution is obtained for functions such as reliability and failure rate, instead of point estimate as in classical statistics. Therefore, in order to obtain a point estimate for these functions, a point on the posterior distributions needs to be calculated. Again, the expected value (mean) or median value are used.
[math]\displaystyle{ pdf }[/math] of the Times-to-Failure
The posterior distribution of the failure time is given by:
- [math]\displaystyle{ f(T|Data)=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }f(T,\beta ,\eta )f(\beta ,\eta |Data)d\eta d\beta }[/math] EQNREF WeibBayesPDF
- where:
- [math]\displaystyle{ f(T,\beta ,\eta )=\dfrac{\beta }{\eta }\left( \dfrac{T}{\eta }\right) ^{\beta -1}e^{-\left( \dfrac{T}{\eta }\right) ^{\beta }} }[/math]
For the [math]\displaystyle{ pdf }[/math] of the times-to-failure, only the expected value is calculated and reported in Weibull++.
Reliability
In order to calculate the median value of the reliability function, we first need to obtain posterior of the reliability. Since R(T) is a function of β, the density functions of β and R(T) have the following relationship:
- [math]\displaystyle{ \begin{align} f(R|Data,T)dR = & f(\beta |Data)d\beta)\\ = & (\int\nolimits_{0}^{\infty }f(\beta ,\eta |Data)d{\eta}) d{\beta} \\ =& \dfrac{\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }d\beta \end{align} }[/math] EQNREF Rpdf
The median value of the reliability is obtained by solving the following equation w.r.t. [math]\displaystyle{ \breve{R}: }[/math]
- [math]\displaystyle{ \int\nolimits_{0}^{\breve{R}}f(R|Data,T)dR=0.5 }[/math] EQNREF MedRel
The expected value of the reliability at time is given by:
- [math]\displaystyle{ R(T|Data)=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }R(T,\beta ,\eta )f(\beta ,\eta |Data)d\eta d\beta }[/math] where:
- [math]\displaystyle{ R(T,\beta ,\eta )=e^{-\left( \dfrac{T}{\eta }\right) ^{^{\beta }}} }[/math]
Failure Rate
The failure rate at time is given by:
- [math]\displaystyle{ \lambda (T|Data)=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\lambda (T,\beta ,\eta )L(\beta ,\eta )\varphi (\eta )\varphi (\beta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
- where:
- [math]\displaystyle{ \lambda (T,\beta ,\eta )=\dfrac{\beta }{\eta }\left( \dfrac{T}{\eta }\right) ^{\beta -1} }[/math]
Note on Calculated Results
As mentioned above, in order to obtain point estimates for the parameters of functions of the parameters in Bayesian analysis, the Median or Mean values of the different posterior [math]\displaystyle{ pdf }[/math]s are calculated. It is important to note that the Median value is preferable and is the default in Weibull++. This is because the Median value always corresponds to the 50th percentile of the distribution. On the other hand, the Mean is not a fixed point on the distribution, which could cause issues, especially when comparing results across different data sets.
Confidence Bounds on R(T)
The confidence bounds calculation under the Weibull-Bayesian analysis is very similar to the Bayesian Confidence Bounds method described in the previous section, with the exception that in the case of the Weibull-Bayesian Analysis the specified prior of β is considered instead of an non-informative prior. The Bayesian one-sided upper bound estimate for R(T) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{U}(T)}f(R|Data,T)dR=CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and (EQNREF Rpdf ) the following is obtained:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{T\exp (-\dfrac{\ln (-\ln R_{U})}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLRU
Eqn. (EQNREF 1CLRU ) can be solved for RU(T). The Bayesian one-sided lower bound estimate for [math]\displaystyle{ \ R(T) }[/math] is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{L}(T)}f(R|Data,T)dR=1-CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and (EQNREF Rpdf ) the following is obtained:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T\exp (-\dfrac{\ln (-\ln R_{L})}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=1-CL }[/math] EQNREF 1CLRL
Eqn. (EQNREF 1CLRL ) can be solved for RL(T). The Bayesian two-sided bounds estimate for R(T) is given by:
- [math]\displaystyle{ \int\nolimits_{R_{L}(T)}^{R_{U}(T)}f(R|Data,T)dR=CL }[/math] which is equivalent to:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{U}(T)}f(R|Data,T)dR=(1+CL)/2 }[/math]
- and
- [math]\displaystyle{ \int\nolimits_{0}^{R_{L}(T)}f(R|Data,T)dR=(1-CL)/2 }[/math]
Using the same method for one-sided bounds, RU(T)and RL(T) can be computed.
Confidence Bounds on Time [math]\displaystyle{ T }[/math]
Following the same procedure described for bounds on Reliability, the bounds of time can be calculated, given . The Bayesian one-sided upper bound estimate for T(R) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{U}(R)}f(T|Data,R)dT=CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and. (EQNREF WeibBayesPDF ), we obtain:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T_{U}\exp (-\dfrac{\ln (-\ln R)}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLTU
Eqn. (EQNREF 1CLTU ) can be solved for TU(R). The Bayesian one-sided lower bound estimate for T(R) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{L}(R)}f(T|Data,R)dT=1-CL }[/math]
- or:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{T_{L}\exp (\dfrac{-\ln (-\ln R)}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLTL
Eqn. (EQNREF 1CLTL ) can be solved for TL(R). The Bayesian two-sided lower bounds estimate for T(R) is:
- [math]\displaystyle{ \int\nolimits_{T_{L}(R)}^{T_{U}(R)}f(T|Data,R)dT=CL }[/math]
which is equivalent to:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{U}(R)}f(T|Data,R)dT=(1+CL)/2 }[/math]
- and:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{L}(R)}f(T|Data,R)dT=(1-CL)/2 }[/math]
Example 6
A manufacturer has tested prototypes of a modified product. The test was terminated at 2000 hours, with only two failures observed from a sample size of eighteen.
| Number of State | State of F or S | State End Time |
|---|---|---|
| 1 | F | 1180 |
| 1 | F | 1842 |
| 16 | S | 2000 |
Because of the lack of failure data in the prototype testing, the manufacturer decided to use information gathered from prior tests on this product to increase the confidence in the results of the prototype testing. This decision was made because failure analysis indicated that the failure mode of these two failures is the same as the one observed in previous tests. In other words, it is expected that the shape of the distribution hasn't changed, but hopefully the scale has, indicating longer life. The two-parameter Weibull distribution have been used to model all prior tests results. The list of the estimated β parameter is as follows:
| Betas Obtained for Similar Mode |
|---|
| 1.7 |
| 2.1 |
| 2.4 |
| 3.1 |
| 3.5 |
First, in order to fit the data to a Weibull-Bayesian model, a prior distribution for β needs to be determined. Based on the prior tests' β values, the prior distribution for β was found to be a lognormal distribution with μ = 0.9064, σ = 0.3325 (obtained by entering the β values into a Weibull++ Standard Folio and analyzing it based on the RRX analysis method.)
the test data is entered into a Standard Folio, the Weibull-Bayesian is selected under Distribution and the β prior distribution is entered after clicking the Calculate button.
Suppose that the reliability at 3000hr is the metric of interest in this example. This reliability can be obtained using Eqn. (EQNREF MedRel ), resulting in the median value of the posterior of the reliability at 3000hr. Using the QCP, this value is calculated to be 76.97. ( By default Weibull++ returns the median values of the posterior distribution. )
The posterior [math]\displaystyle{ pdf }[/math] of the reliability function at 3000hrs can be obtained using Eqn. (EQNREF Rpdf ). In Figure 6-10 the posterior [math]\displaystyle{ pdf }[/math] of the reliability at 3000hrs is plotted, with the corresponding median value as well as the 10th percentile value shown. The 10th percentile constitutes the 90 Lower 1-Sided bound on the reliability at 3000hrs, which is calculated to be 50.77.
Notice that the [math]\displaystyle{ pdf }[/math] plotted in Fig. 6-10 is of the reliability at 3000hrs, and not the [math]\displaystyle{ pdf }[/math] of the times-to-failure data. The [math]\displaystyle{ pdf }[/math] of the times-to-failure data can be obtained using Eqn. (EQNREF WeibBayesPDF ) and plotted using Weibull++, as shown next:
| The material on this page is copyrighted. | ©1992-2012. ReliaSoft Corporation. ALL RIGHTS RESERVED. |
The Weibull Distribution
The Weibull distribution is one of the most widely used lifetime distributions in reliability engineering. It is a versatile distribution that can take on the characteristics of other types of distributions, based on the value of the shape parameter, [math]\displaystyle{ \boldsymbol{\beta} }[/math]. This chapter provides a brief background on the Weibull distribution, presents and derives most of the applicable equations and presents examples calculated both manually and by using ReliaSoft's Weibull++.
Template loop detected: Template:Weibull Probability Density Function
The Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} \,\! }[/math], (also called MTTF) of the Weibull pdf is given by:
- [math]\displaystyle{ \overline{T}=\gamma +\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
where
- [math]\displaystyle{ \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
is the gamma function evaluated at the value of:
- [math]\displaystyle{ \left( { \frac{1}{\beta }}+1\right) \,\! }[/math]
The gamma function is defined as:
- [math]\displaystyle{ \Gamma (n)=\int_{0}^{\infty }e^{-x}x^{n-1}dx \,\! }[/math]
For the 2-parameter case, this can be reduced to:
- [math]\displaystyle{ \overline{T}=\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
Note that some practitioners erroneously assume that [math]\displaystyle{ \eta \,\! }[/math] is equal to the MTTF, [math]\displaystyle{ \overline{T}\,\! }[/math]. This is only true for the case of: [math]\displaystyle{ \beta=1 \,\! }[/math] or:
- [math]\displaystyle{ \begin{align} \overline{T} &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {2}\right) \\ &= \eta \cdot 1\\ &= \eta \end{align} \,\! }[/math]
The Median
The median, [math]\displaystyle{ \breve{T}\,\! }[/math], of the Weibull distribution is given by:
- [math]\displaystyle{ \breve{T}=\gamma +\eta \left( \ln 2\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Mode
The mode, [math]\displaystyle{ \tilde{T} \,\! }[/math], is given by:
- [math]\displaystyle{ \tilde{T}=\gamma +\eta \left( 1-\frac{1}{\beta }\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Standard Deviation
The standard deviation, [math]\displaystyle{ \sigma _{T}\,\! }[/math], is given by:
- [math]\displaystyle{ \sigma _{T}=\eta \cdot \sqrt{\Gamma \left( {\frac{2}{\beta }}+1\right) -\Gamma \left( {\frac{1}{ \beta }}+1\right) ^{2}} \,\! }[/math]
The Weibull Reliability Function
The equation for the 3-parameter Weibull cumulative density function, cdf, is given by:
- [math]\displaystyle{ F(t)=1-e^{-\left( \frac{t-\gamma }{\eta }\right) ^{\beta }} \,\! }[/math]
This is also referred to as unreliability and designated as [math]\displaystyle{ Q(t) \,\! }[/math] by some authors.
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function for the 3-parameter Weibull distribution is then given by:
- [math]\displaystyle{ R(t)=e^{-\left( { \frac{t-\gamma }{\eta }}\right) ^{\beta }} \,\! }[/math]
The Weibull Conditional Reliability Function
The 3-parameter Weibull conditional reliability function is given by:
- [math]\displaystyle{ R(t|T)={ \frac{R(T+t)}{R(T)}}={\frac{e^{-\left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }}}{e^{-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }}}} \,\! }[/math]
or:
- [math]\displaystyle{ R(t|T)=e^{-\left[ \left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }\right] } \,\! }[/math]
These give the reliability for a new mission of [math]\displaystyle{ t \,\! }[/math] duration, having already accumulated [math]\displaystyle{ T \,\! }[/math] time of operation up to the start of this new mission, and the units are checked out to assure that they will start the next mission successfully. It is called conditional because you can calculate the reliability of a new mission based on the fact that the unit or units already accumulated hours of operation successfully.
The Weibull Reliable Life
The reliable life, [math]\displaystyle{ T_{R}\,\! }[/math], of a unit for a specified reliability, [math]\displaystyle{ R\,\! }[/math], starting the mission at age zero, is given by:
- [math]\displaystyle{ T_{R}=\gamma +\eta \cdot \left\{ -\ln ( R ) \right\} ^{ \frac{1}{\beta }} \,\! }[/math]
This is the life for which the unit/item will be functioning successfully with a reliability of [math]\displaystyle{ R\,\! }[/math]. If [math]\displaystyle{ R = 0.50\,\! }[/math], then [math]\displaystyle{ T_{R}=\breve{T} \,\! }[/math], the median life, or the life by which half of the units will survive.
The Weibull Failure Rate Function
The Weibull failure rate function, [math]\displaystyle{ \lambda(t) \,\! }[/math], is given by:
- [math]\displaystyle{ \lambda \left( t\right) = \frac{f\left( t\right) }{R\left( t\right) }=\frac{\beta }{\eta }\left( \frac{ t-\gamma }{\eta }\right) ^{\beta -1} \,\! }[/math]
The Weibull distribution is widely used in reliability and life data analysis due to its versatility. Depending on the values of the parameters, the Weibull distribution can be used to model a variety of life behaviors. We will now examine how the values of the shape parameter, [math]\displaystyle{ \beta\,\! }[/math], and the scale parameter, [math]\displaystyle{ \eta\,\! }[/math], affect such distribution characteristics as the shape of the curve, the reliability and the failure rate. Note that in the rest of this section we will assume the most general form of the Weibull distribution, (i.e., the 3-parameter form). The appropriate substitutions to obtain the other forms, such as the 2-parameter form where [math]\displaystyle{ \gamma = 0,\,\! }[/math] or the 1-parameter form where [math]\displaystyle{ \beta = C = \,\! }[/math] constant, can easily be made.
Effects of the Shape Parameter, beta
The Weibull shape parameter, [math]\displaystyle{ \beta\,\! }[/math], is also known as the slope. This is because the value of [math]\displaystyle{ \beta\,\! }[/math] is equal to the slope of the regressed line in a probability plot. Different values of the shape parameter can have marked effects on the behavior of the distribution. In fact, some values of the shape parameter will cause the distribution equations to reduce to those of other distributions. For example, when [math]\displaystyle{ \beta = 1\,\! }[/math], the pdf of the 3-parameter Weibull distribution reduces to that of the 2-parameter exponential distribution or:
- [math]\displaystyle{ f(t)={\frac{1}{\eta }}e^{-{\frac{t-\gamma }{\eta }}} \,\! }[/math]
where [math]\displaystyle{ \frac{1}{\eta }=\lambda = \,\! }[/math] failure rate. The parameter [math]\displaystyle{ \beta\,\! }[/math] is a pure number, (i.e., it is dimensionless). The following figure shows the effect of different values of the shape parameter, [math]\displaystyle{ \beta\,\! }[/math], on the shape of the pdf. As you can see, the shape can take on a variety of forms based on the value of [math]\displaystyle{ \beta\,\! }[/math].
For [math]\displaystyle{ 0\lt \beta \leq 1 \,\! }[/math]:
- As [math]\displaystyle{ t \rightarrow 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\! }[/math]), [math]\displaystyle{ f(t)\rightarrow \infty.\,\! }[/math]
- As [math]\displaystyle{ t\rightarrow \infty\,\! }[/math], [math]\displaystyle{ f(t)\rightarrow 0\,\! }[/math].
- [math]\displaystyle{ f(t)\,\! }[/math] decreases monotonically and is convex as it increases beyond the value of [math]\displaystyle{ \gamma\,\! }[/math].
- The mode is non-existent.
For [math]\displaystyle{ \beta \gt 1 \,\! }[/math]:
- [math]\displaystyle{ f(t) = 0\,\! }[/math] at [math]\displaystyle{ t = 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\! }[/math]).
- [math]\displaystyle{ f(t)\,\! }[/math] increases as [math]\displaystyle{ t\rightarrow \tilde{T} \,\! }[/math] (the mode) and decreases thereafter.
- For [math]\displaystyle{ \beta \lt 2.6\,\! }[/math] the Weibull pdf is positively skewed (has a right tail), for [math]\displaystyle{ 2.6 \lt \beta \lt 3.7\,\! }[/math] its coefficient of skewness approaches zero (no tail). Consequently, it may approximate the normal pdf, and for [math]\displaystyle{ \beta \gt 3.7\,\! }[/math] it is negatively skewed (left tail). The way the value of [math]\displaystyle{ \beta\,\! }[/math] relates to the physical behavior of the items being modeled becomes more apparent when we observe how its different values affect the reliability and failure rate functions. Note that for [math]\displaystyle{ \beta = 0.999\,\! }[/math], [math]\displaystyle{ f(0) = \infty\,\! }[/math], but for [math]\displaystyle{ \beta = 1.001\,\! }[/math], [math]\displaystyle{ f(0) = 0.\,\! }[/math] This abrupt shift is what complicates MLE estimation when [math]\displaystyle{ \beta\,\! }[/math] is close to 1.
The Effect of beta on the cdf and Reliability Function
The above figure shows the effect of the value of [math]\displaystyle{ \beta\,\! }[/math] on the cdf, as manifested in the Weibull probability plot. It is easy to see why this parameter is sometimes referred to as the slope. Note that the models represented by the three lines all have the same value of [math]\displaystyle{ \eta\,\! }[/math]. The following figure shows the effects of these varied values of [math]\displaystyle{ \beta\,\! }[/math] on the reliability plot, which is a linear analog of the probability plot.
- [math]\displaystyle{ R(t)\,\! }[/math] decreases sharply and monotonically for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] and is convex.
- For [math]\displaystyle{ \beta = 1\,\! }[/math], [math]\displaystyle{ R(t)\,\! }[/math] decreases monotonically but less sharply than for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] and is convex.
- For [math]\displaystyle{ \beta \gt 1\,\! }[/math], [math]\displaystyle{ R(t)\,\! }[/math] decreases as increases. As wear-out sets in, the curve goes through an inflection point and decreases sharply.
The Effect of beta on the Weibull Failure Rate
The value of [math]\displaystyle{ \beta\,\! }[/math] has a marked effect on the failure rate of the Weibull distribution and inferences can be drawn about a population's failure characteristics just by considering whether the value of [math]\displaystyle{ \beta\,\! }[/math] is less than, equal to, or greater than one.
As indicated by above figure, populations with [math]\displaystyle{ \beta \lt 1\,\! }[/math] exhibit a failure rate that decreases with time, populations with [math]\displaystyle{ \beta = 1\,\! }[/math] have a constant failure rate (consistent with the exponential distribution) and populations with [math]\displaystyle{ \beta \gt 1\,\! }[/math] have a failure rate that increases with time. All three life stages of the bathtub curve can be modeled with the Weibull distribution and varying values of [math]\displaystyle{ \beta\,\! }[/math]. The Weibull failure rate for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] is unbounded at [math]\displaystyle{ T = 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\!)\,\! }[/math]. The failure rate, [math]\displaystyle{ \lambda(t),\,\! }[/math] decreases thereafter monotonically and is convex, approaching the value of zero as [math]\displaystyle{ t\rightarrow \infty\,\! }[/math] or [math]\displaystyle{ \lambda (\infty) = 0\,\! }[/math]. This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When encountering such behavior in a manufactured product, it may be indicative of problems in the production process, inadequate burn-in, substandard parts and components, or problems with packaging and shipping. For [math]\displaystyle{ \beta = 1\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] yields a constant value of [math]\displaystyle{ { \frac{1}{\eta }} \,\! }[/math] or:
- [math]\displaystyle{ \lambda (t)=\lambda ={\frac{1}{\eta }} \,\! }[/math]
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
For [math]\displaystyle{ \beta \gt 1\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] increases as [math]\displaystyle{ t\,\! }[/math] increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For [math]\displaystyle{ 1 \lt \beta \lt 2,\,\! }[/math] the [math]\displaystyle{ \lambda(t)\,\! }[/math] curve is concave, consequently the failure rate increases at a decreasing rate as [math]\displaystyle{ t\,\! }[/math] increases.
For [math]\displaystyle{ \beta = 2\,\! }[/math] there emerges a straight line relationship between [math]\displaystyle{ \lambda(t)\,\! }[/math] and [math]\displaystyle{ t\,\! }[/math], starting at a value of [math]\displaystyle{ \lambda(t) = 0\,\! }[/math] at [math]\displaystyle{ t = \gamma\,\! }[/math], and increasing thereafter with a slope of [math]\displaystyle{ { \frac{2}{\eta ^{2}}} \,\! }[/math]. Consequently, the failure rate increases at a constant rate as [math]\displaystyle{ t\,\! }[/math] increases. Furthermore, if [math]\displaystyle{ \eta = 1\,\! }[/math] the slope becomes equal to 2, and when [math]\displaystyle{ \gamma = 0\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] becomes a straight line which passes through the origin with a slope of 2. Note that at [math]\displaystyle{ \beta = 2\,\! }[/math], the Weibull distribution equations reduce to that of the Rayleigh distribution.
When [math]\displaystyle{ \beta \gt 2,\,\! }[/math] the [math]\displaystyle{ \lambda(t)\,\! }[/math] curve is convex, with its slope increasing as [math]\displaystyle{ t\,\! }[/math] increases. Consequently, the failure rate increases at an increasing rate as [math]\displaystyle{ t\,\! }[/math] increases, indicating wearout life.
Effects of the Scale Parameter, eta
A change in the scale parameter [math]\displaystyle{ \eta\,\! }[/math] has the same effect on the distribution as a change of the abscissa scale. Increasing the value of [math]\displaystyle{ \eta\,\! }[/math] while holding [math]\displaystyle{ \beta\,\! }[/math] constant has the effect of stretching out the pdf. Since the area under a pdf curve is a constant value of one, the "peak" of the pdf curve will also decrease with the increase of [math]\displaystyle{ \eta\,\! }[/math], as indicated in the above figure.
- If [math]\displaystyle{ \eta\,\! }[/math] is increased while [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math] are kept the same, the distribution gets stretched out to the right and its height decreases, while maintaining its shape and location.
- If [math]\displaystyle{ \eta\,\! }[/math] is decreased while [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math] are kept the same, the distribution gets pushed in towards the left (i.e., towards its beginning or towards 0 or [math]\displaystyle{ \gamma\,\! }[/math]), and its height increases.
- [math]\displaystyle{ \eta\,\! }[/math] has the same units as [math]\displaystyle{ t\,\! }[/math], such as hours, miles, cycles, actuations, etc.
Effects of the Location Parameter, gamma
The location parameter, [math]\displaystyle{ \gamma\,\! }[/math], as the name implies, locates the distribution along the abscissa. Changing the value of [math]\displaystyle{ \gamma\,\! }[/math] has the effect of sliding the distribution and its associated function either to the right (if [math]\displaystyle{ \gamma \gt 0\,\! }[/math]) or to the left (if [math]\displaystyle{ \gamma \lt 0\,\! }[/math]).
- When [math]\displaystyle{ \gamma = 0,\,\! }[/math] the distribution starts at [math]\displaystyle{ t=0\,\! }[/math] or at the origin.
- If [math]\displaystyle{ \gamma \gt 0,\,\! }[/math] the distribution starts at the location [math]\displaystyle{ \gamma\,\! }[/math] to the right of the origin.
- If [math]\displaystyle{ \gamma \lt 0,\,\! }[/math] the distribution starts at the location [math]\displaystyle{ \gamma\,\! }[/math] to the left of the origin.
- [math]\displaystyle{ \gamma\,\! }[/math] provides an estimate of the earliest time-to-failure of such units.
- The life period 0 to [math]\displaystyle{ + \gamma\,\! }[/math] is a failure free operating period of such units.
- The parameter [math]\displaystyle{ \gamma\,\! }[/math] may assume all values and provides an estimate of the earliest time a failure may be observed. A negative [math]\displaystyle{ \gamma\,\! }[/math] may indicate that failures have occurred prior to the beginning of the test, namely during production, in storage, in transit, during checkout prior to the start of a mission, or prior to actual use.
- [math]\displaystyle{ \gamma\,\! }[/math] has the same units as [math]\displaystyle{ t\,\! }[/math], such as hours, miles, cycles, actuations, etc.
Template loop detected: Template:Estimation of the Weibull Parameters
Template loop detected: Template:Weibull fisher matrix confidence bounds
Likelihood Ratio Confidence Bounds
As covered in Chapter 5, the likelihood confidence bounds are calculated by finding values for θ1 and θ2 that satisfy:
- [math]\displaystyle{ -2\cdot \text{ln}\left( \frac{L(\theta _{1},\theta _{2})}{L(\hat{\theta }_{1}, \hat{\theta }_{2})}\right) =\chi _{\alpha ;1}^{2} EQNREF lratio2 }[/math]
This equation can be rewritten as:
- [math]\displaystyle{ L(\theta _{1},\theta _{2})=L(\hat{\theta }_{1},\hat{\theta } _{2})\cdot e^{\frac{-\chi _{\alpha ;1}^{2}}{2}} EQNREF lratio3 }[/math]
For complete data, the likelihood function for the Weibull distribution is given by:
- [math]\displaystyle{ L(\beta ,\eta )=\prod_{i=1}^{N}f(x_{i};\beta ,\eta )=\prod_{i=1}^{N}\frac{ \beta }{\eta }\cdot \left( \frac{x_{i}}{\eta }\right) ^{\beta -1}\cdot e^{-\left( \frac{x_{i}}{\eta }\right) ^{\beta }} }[/math]
For a given value of α, values for β and η can be found which represent the maximum and minimum values that satisfy Eqn. (\ref {lratio3}). These represent the confidence bounds for the parameters at a confidence level δ, where α = δ for two-sided bounds and α = 2δ − 1 for one-sided.
Similarly, the bounds on time and reliability can be found by substituting the Weibull reliability equation into the likelihood function so that it is in terms of β and time or reliability, as discussed in Chapter 5. The likelihood ratio equation used to solve for bounds on time (Type 1) is:
- [math]\displaystyle{ L(\beta ,t)=\prod_{i=1}^{N}\frac{\beta }{\left( \frac{t}{(-\text{ln}(R))^{ \frac{1}{\beta }}}\right) }\cdot \left( \frac{x_{i}}{\left( \frac{t}{(-\text{ ln}(R))^{\frac{1}{\beta }}}\right) }\right) ^{\beta -1}\cdot \text{exp}\left[ -\left( \frac{x_{i}}{\left( \frac{t}{(-\text{ln}(R))^{\frac{1}{\beta }}} \right) }\right) ^{\beta }\right] }[/math]
The likelihood ratio equation used to solve for bounds on reliability (Type 2) is:
- [math]\displaystyle{ L(\beta ,R)=\prod_{i=1}^{N}\frac{\beta }{\left( \frac{t}{(-\text{ln}(R))^{ \frac{1}{\beta }}}\right) }\cdot \left( \frac{x_{i}}{\left( \frac{t}{(-\text{ ln}(R))^{\frac{1}{\beta }}}\right) }\right) ^{\beta -1}\cdot \text{exp}\left[ -\left( \frac{x_{i}}{\left( \frac{t}{(-\text{ln}(R))^{\frac{1}{\beta }}} \right) }\right) ^{\beta }\right] }[/math]
Bayesian Confidence Bounds
Bounds on Parameters
Bayesian Bounds use non-informative prior distributions for both parameters. From Chapter 5, we know that if the prior distribution of η and β are independent, the posterior joint distribution of η and β can be written as:
- [math]\displaystyle{ f(\eta ,\beta |Data)= \dfrac{L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )}{\int_{0}^{\infty }\int_{0}^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
The marginal distribution of η is:
- [math]\displaystyle{ f(\eta |Data) =\int_{0}^{\infty }f(\eta ,\beta |Data)d\beta = \dfrac{\int_{0}^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\beta }{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
where: [math]\displaystyle{ \varphi (\beta )=\frac{1}{\beta } }[/math] is the non-informative prior of β. [math]\displaystyle{ \varphi (\eta )=\frac{1}{\eta } }[/math] is the non-informative prior of η. Using these non-informative prior distributions, [math]\displaystyle{ f(\eta|Data) }[/math] can be rewritten as:
- [math]\displaystyle{ f(\eta |Data)=\dfrac{\int_{0}^{\infty }L(Data|\eta ,\beta )\frac{1}{\beta } \frac{1}{\eta }d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(Data|\eta ,\beta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } }[/math]
The one-sided upper bounds of η is:
- [math]\displaystyle{ CL=P(\eta \leq \eta _{U})=\int_{0}^{\eta _{U}}f(\eta |Data)d\eta }[/math]
The one-sided lower bounds of η is:
- [math]\displaystyle{ 1-CL=P(\eta \leq \eta _{L})=\int_{0}^{\eta _{L}}f(\eta |Data)d\eta }[/math] The two-sided bounds of η is:
- [math]\displaystyle{ CL=P(\eta _{L}\leq \eta \leq \eta _{U})=\int_{\eta _{L}}^{\eta _{U}}f(\eta |Data)d\eta }[/math] Same method is used to obtain the bounds of β.
Bounds on Time (Type 1)
From Chapter 5, we know that:
- [math]\displaystyle{ CL=\Pr (T\leq T_{U})=\Pr (\eta \leq T_{U}\exp (-\frac{\ln (-\ln R)}{\beta })) }[/math] From the posterior distribution of η, we have:
- [math]\displaystyle{ CL=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T_{U}\exp (-\dfrac{ \ln (-\ln R)}{\beta })}L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } EQNREF BayesCLT }[/math]
Eqn. (EQNREF BayesCLT ) is solved numerically for TU. The same method can be applied to calculate one sided lower bounds and two-sided bounds on time.
Bounds on Reliability (Type 2)
- [math]\displaystyle{ CL=\Pr (R\leq R_{U})=\Pr (\eta \leq T\exp (-\frac{\ln (-\ln R_{U})}{\beta })) }[/math] From the posterior distribution of η, we have:
- [math]\displaystyle{ CL=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T\exp (-\dfrac{\ln (-\ln R_{U})}{\beta })}L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } EQNREF BayesCLR }[/math]
Eqn. (EQNREF BayesCLR ) is solved numerically for RU. The same method can be used to calculate the one sided lower bounds and two-sided bounds on reliability.
Weibull-Bayesian Analysis
In this section, the Bayesian methods are presented for the two-parameter Weibull distribution. Bayesian concepts were introduced in Chapter 3. This model considers prior knowledge on the shape (β) parameter of the Weibull distribution when it is chosen to be fitted to a given set of data. There are many practical applications for this model, particularly when dealing with small sample sizes and some prior knowledge for the shape parameter is available. For example, when a test is performed, there is often a good understanding about the behavior of the failure mode under investigation, primarily through historical data. At the same time, most reliability tests are performed on a limited number of samples. Under these conditions, it would be very useful to use this prior knowledge with the goal of making more accurate predictions. A common approach for such scenarios is to use the one-parameter Weibull distribution, but this approach is too deterministic, too absolute you may say (and you would be right). The Weibull-Bayesian model in Weibull++ (which is actually a true "WeiBayes" model, unlike the one-parameter Weibull that is commonly referred to as such) offers an alternative to the one-parameter Weibull, by including the variation and uncertainty that might have been observed in the past on the shape parameter. Applying Bayes's rule on the two-parameter Weibull distribution and assuming the prior distributions of β and η are independent, we obtain the following posterior :
- [math]\displaystyle{ f(\beta ,\eta |Data)=\dfrac{L(\beta ,\eta )\varphi (\beta )\varphi (\eta )}{ \int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math] EQNREF WeibBayes
In this model, η is assumed to follow a noninformative prior distribution with the density function [math]\displaystyle{ \varphi (\eta )=\dfrac{1}{\eta } }[/math]. This is called Jeffrey's prior, and is obtained by performing a logarithmic transformation on η. Specifically, since η is always positive, we can assume that ln(η) follows a uniform distribution, U( − ∞, + ∞). Applying Jeffrey's rule [9] which says "in general, an approximate non-informative prior is taken proportional to the square root of Fisher's information", yields [math]\displaystyle{ \varphi (\eta )=\dfrac{1}{\eta }. }[/math]
The prior distribution of β, denoted as [math]\displaystyle{ \varphi (\beta ) }[/math], can be selected from the following distributions: normal, lognormal, exponential and uniform. The procedure of performing a Weibull-Bayesian analysis is as follows:
- Collect the times-to-failure data.
- Specify a prior distribution for β (the prior for η is assumed to be 1/η).
- Obtain the posterior from Eqn. (EQNREF WeibBayes ).
In other words, a distribution (the posterior ) is obtained, rather than a point estimate as in classical statistics (i.e., as in the parameter estimation methods described previously in this chapter). Therefore, if a point estimate needs to be reported, a point of the posterior needs to be calculated. Typical points of the posterior distribution used are the mean (expected value) or median. In Weibull++, both options are available and can be chosen from the Analysis page, under the Results As area, as shown next.
The expected value of β is obtained by:
- [math]\displaystyle{ E(\beta )=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\beta \cdot f(\beta ,\eta |Data)d\beta d\eta }[/math]
Similarly, the expected value of η is obtained by:
- [math]\displaystyle{ E(\eta )=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\eta \cdot f(\beta ,\eta |Data)d\beta d\eta }[/math]
The median points are obtained by solving the following equations for [math]\displaystyle{ \breve{\beta} }[/math] and [math]\displaystyle{ \breve{\eta} }[/math] respectively:
- [math]\displaystyle{ \int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\breve{\beta}}f(\beta ,\eta |Data)d\beta d\eta =0.5 }[/math]
- and
- [math]\displaystyle{ \int\nolimits_{0}^{\breve{\eta}}\int\nolimits_{0}^{\infty }f(\beta ,\eta |Data)d\beta d\eta =0.5 }[/math]
Of course, other points of the posterior distribution can be calculated as well. For example, one may want to calculate the 10th percentile of the joint posterior distribution (w.r.t. one of the parameters). The procedure for obtaining other points of the posterior distribution is similar to the one for obtaining the median values, where instead of 0.5 the percentage of interest is given. This procedure actually provides the confidence bounds on the parameters, which in the Bayesian framework are called ‘‘Credible Bounds‘‘. However, since the engineering interpretation is the same, and to avoid confusion, we refer to them as confidence bounds in this reference and in Weibull++.
Posterior Distributions for Functions of Parameters
As explained in Chapter 3, in Bayesian analysis, all the functions of the parameters are distributed. In other words, a posterior distribution is obtained for functions such as reliability and failure rate, instead of point estimate as in classical statistics. Therefore, in order to obtain a point estimate for these functions, a point on the posterior distributions needs to be calculated. Again, the expected value (mean) or median value are used.
[math]\displaystyle{ pdf }[/math] of the Times-to-Failure
The posterior distribution of the failure time is given by:
- [math]\displaystyle{ f(T|Data)=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }f(T,\beta ,\eta )f(\beta ,\eta |Data)d\eta d\beta }[/math] EQNREF WeibBayesPDF
- where:
- [math]\displaystyle{ f(T,\beta ,\eta )=\dfrac{\beta }{\eta }\left( \dfrac{T}{\eta }\right) ^{\beta -1}e^{-\left( \dfrac{T}{\eta }\right) ^{\beta }} }[/math]
For the [math]\displaystyle{ pdf }[/math] of the times-to-failure, only the expected value is calculated and reported in Weibull++.
Reliability
In order to calculate the median value of the reliability function, we first need to obtain posterior of the reliability. Since R(T) is a function of β, the density functions of β and R(T) have the following relationship:
- [math]\displaystyle{ \begin{align} f(R|Data,T)dR = & f(\beta |Data)d\beta)\\ = & (\int\nolimits_{0}^{\infty }f(\beta ,\eta |Data)d{\eta}) d{\beta} \\ =& \dfrac{\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }d\beta \end{align} }[/math] EQNREF Rpdf
The median value of the reliability is obtained by solving the following equation w.r.t. [math]\displaystyle{ \breve{R}: }[/math]
- [math]\displaystyle{ \int\nolimits_{0}^{\breve{R}}f(R|Data,T)dR=0.5 }[/math] EQNREF MedRel
The expected value of the reliability at time is given by:
- [math]\displaystyle{ R(T|Data)=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }R(T,\beta ,\eta )f(\beta ,\eta |Data)d\eta d\beta }[/math] where:
- [math]\displaystyle{ R(T,\beta ,\eta )=e^{-\left( \dfrac{T}{\eta }\right) ^{^{\beta }}} }[/math]
Failure Rate
The failure rate at time is given by:
- [math]\displaystyle{ \lambda (T|Data)=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\lambda (T,\beta ,\eta )L(\beta ,\eta )\varphi (\eta )\varphi (\beta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
- where:
- [math]\displaystyle{ \lambda (T,\beta ,\eta )=\dfrac{\beta }{\eta }\left( \dfrac{T}{\eta }\right) ^{\beta -1} }[/math]
Note on Calculated Results
As mentioned above, in order to obtain point estimates for the parameters of functions of the parameters in Bayesian analysis, the Median or Mean values of the different posterior [math]\displaystyle{ pdf }[/math]s are calculated. It is important to note that the Median value is preferable and is the default in Weibull++. This is because the Median value always corresponds to the 50th percentile of the distribution. On the other hand, the Mean is not a fixed point on the distribution, which could cause issues, especially when comparing results across different data sets.
Confidence Bounds on R(T)
The confidence bounds calculation under the Weibull-Bayesian analysis is very similar to the Bayesian Confidence Bounds method described in the previous section, with the exception that in the case of the Weibull-Bayesian Analysis the specified prior of β is considered instead of an non-informative prior. The Bayesian one-sided upper bound estimate for R(T) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{U}(T)}f(R|Data,T)dR=CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and (EQNREF Rpdf ) the following is obtained:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{T\exp (-\dfrac{\ln (-\ln R_{U})}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLRU
Eqn. (EQNREF 1CLRU ) can be solved for RU(T). The Bayesian one-sided lower bound estimate for [math]\displaystyle{ \ R(T) }[/math] is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{L}(T)}f(R|Data,T)dR=1-CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and (EQNREF Rpdf ) the following is obtained:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T\exp (-\dfrac{\ln (-\ln R_{L})}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=1-CL }[/math] EQNREF 1CLRL
Eqn. (EQNREF 1CLRL ) can be solved for RL(T). The Bayesian two-sided bounds estimate for R(T) is given by:
- [math]\displaystyle{ \int\nolimits_{R_{L}(T)}^{R_{U}(T)}f(R|Data,T)dR=CL }[/math] which is equivalent to:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{U}(T)}f(R|Data,T)dR=(1+CL)/2 }[/math]
- and
- [math]\displaystyle{ \int\nolimits_{0}^{R_{L}(T)}f(R|Data,T)dR=(1-CL)/2 }[/math]
Using the same method for one-sided bounds, RU(T)and RL(T) can be computed.
Confidence Bounds on Time [math]\displaystyle{ T }[/math]
Following the same procedure described for bounds on Reliability, the bounds of time can be calculated, given . The Bayesian one-sided upper bound estimate for T(R) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{U}(R)}f(T|Data,R)dT=CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and. (EQNREF WeibBayesPDF ), we obtain:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T_{U}\exp (-\dfrac{\ln (-\ln R)}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLTU
Eqn. (EQNREF 1CLTU ) can be solved for TU(R). The Bayesian one-sided lower bound estimate for T(R) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{L}(R)}f(T|Data,R)dT=1-CL }[/math]
- or:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{T_{L}\exp (\dfrac{-\ln (-\ln R)}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLTL
Eqn. (EQNREF 1CLTL ) can be solved for TL(R). The Bayesian two-sided lower bounds estimate for T(R) is:
- [math]\displaystyle{ \int\nolimits_{T_{L}(R)}^{T_{U}(R)}f(T|Data,R)dT=CL }[/math]
which is equivalent to:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{U}(R)}f(T|Data,R)dT=(1+CL)/2 }[/math]
- and:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{L}(R)}f(T|Data,R)dT=(1-CL)/2 }[/math]
Example 6
A manufacturer has tested prototypes of a modified product. The test was terminated at 2000 hours, with only two failures observed from a sample size of eighteen.
| Number of State | State of F or S | State End Time |
|---|---|---|
| 1 | F | 1180 |
| 1 | F | 1842 |
| 16 | S | 2000 |
Because of the lack of failure data in the prototype testing, the manufacturer decided to use information gathered from prior tests on this product to increase the confidence in the results of the prototype testing. This decision was made because failure analysis indicated that the failure mode of these two failures is the same as the one observed in previous tests. In other words, it is expected that the shape of the distribution hasn't changed, but hopefully the scale has, indicating longer life. The two-parameter Weibull distribution have been used to model all prior tests results. The list of the estimated β parameter is as follows:
| Betas Obtained for Similar Mode |
|---|
| 1.7 |
| 2.1 |
| 2.4 |
| 3.1 |
| 3.5 |
First, in order to fit the data to a Weibull-Bayesian model, a prior distribution for β needs to be determined. Based on the prior tests' β values, the prior distribution for β was found to be a lognormal distribution with μ = 0.9064, σ = 0.3325 (obtained by entering the β values into a Weibull++ Standard Folio and analyzing it based on the RRX analysis method.)
the test data is entered into a Standard Folio, the Weibull-Bayesian is selected under Distribution and the β prior distribution is entered after clicking the Calculate button.
Suppose that the reliability at 3000hr is the metric of interest in this example. This reliability can be obtained using Eqn. (EQNREF MedRel ), resulting in the median value of the posterior of the reliability at 3000hr. Using the QCP, this value is calculated to be 76.97. ( By default Weibull++ returns the median values of the posterior distribution. )
The posterior [math]\displaystyle{ pdf }[/math] of the reliability function at 3000hrs can be obtained using Eqn. (EQNREF Rpdf ). In Figure 6-10 the posterior [math]\displaystyle{ pdf }[/math] of the reliability at 3000hrs is plotted, with the corresponding median value as well as the 10th percentile value shown. The 10th percentile constitutes the 90 Lower 1-Sided bound on the reliability at 3000hrs, which is calculated to be 50.77.
Notice that the [math]\displaystyle{ pdf }[/math] plotted in Fig. 6-10 is of the reliability at 3000hrs, and not the [math]\displaystyle{ pdf }[/math] of the times-to-failure data. The [math]\displaystyle{ pdf }[/math] of the times-to-failure data can be obtained using Eqn. (EQNREF WeibBayesPDF ) and plotted using Weibull++, as shown next:
| The material on this page is copyrighted. | ©1992-2012. ReliaSoft Corporation. ALL RIGHTS RESERVED. |
Likelihood Ratio Confidence Bounds
As covered in Chapter 5, the likelihood confidence bounds are calculated by finding values for θ1 and θ2 that satisfy:
- [math]\displaystyle{ -2\cdot \text{ln}\left( \frac{L(\theta _{1},\theta _{2})}{L(\hat{\theta }_{1}, \hat{\theta }_{2})}\right) =\chi _{\alpha ;1}^{2} EQNREF lratio2 }[/math]
This equation can be rewritten as:
- [math]\displaystyle{ L(\theta _{1},\theta _{2})=L(\hat{\theta }_{1},\hat{\theta } _{2})\cdot e^{\frac{-\chi _{\alpha ;1}^{2}}{2}} EQNREF lratio3 }[/math]
For complete data, the likelihood function for the Weibull distribution is given by:
- [math]\displaystyle{ L(\beta ,\eta )=\prod_{i=1}^{N}f(x_{i};\beta ,\eta )=\prod_{i=1}^{N}\frac{ \beta }{\eta }\cdot \left( \frac{x_{i}}{\eta }\right) ^{\beta -1}\cdot e^{-\left( \frac{x_{i}}{\eta }\right) ^{\beta }} }[/math]
For a given value of α, values for β and η can be found which represent the maximum and minimum values that satisfy Eqn. (\ref {lratio3}). These represent the confidence bounds for the parameters at a confidence level δ, where α = δ for two-sided bounds and α = 2δ − 1 for one-sided.
Similarly, the bounds on time and reliability can be found by substituting the Weibull reliability equation into the likelihood function so that it is in terms of β and time or reliability, as discussed in Chapter 5. The likelihood ratio equation used to solve for bounds on time (Type 1) is:
- [math]\displaystyle{ L(\beta ,t)=\prod_{i=1}^{N}\frac{\beta }{\left( \frac{t}{(-\text{ln}(R))^{ \frac{1}{\beta }}}\right) }\cdot \left( \frac{x_{i}}{\left( \frac{t}{(-\text{ ln}(R))^{\frac{1}{\beta }}}\right) }\right) ^{\beta -1}\cdot \text{exp}\left[ -\left( \frac{x_{i}}{\left( \frac{t}{(-\text{ln}(R))^{\frac{1}{\beta }}} \right) }\right) ^{\beta }\right] }[/math]
The likelihood ratio equation used to solve for bounds on reliability (Type 2) is:
- [math]\displaystyle{ L(\beta ,R)=\prod_{i=1}^{N}\frac{\beta }{\left( \frac{t}{(-\text{ln}(R))^{ \frac{1}{\beta }}}\right) }\cdot \left( \frac{x_{i}}{\left( \frac{t}{(-\text{ ln}(R))^{\frac{1}{\beta }}}\right) }\right) ^{\beta -1}\cdot \text{exp}\left[ -\left( \frac{x_{i}}{\left( \frac{t}{(-\text{ln}(R))^{\frac{1}{\beta }}} \right) }\right) ^{\beta }\right] }[/math]
Bayesian Confidence Bounds
Bounds on Parameters
Bayesian Bounds use non-informative prior distributions for both parameters. From Chapter 5, we know that if the prior distribution of η and β are independent, the posterior joint distribution of η and β can be written as:
- [math]\displaystyle{ f(\eta ,\beta |Data)= \dfrac{L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )}{\int_{0}^{\infty }\int_{0}^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
The marginal distribution of η is:
- [math]\displaystyle{ f(\eta |Data) =\int_{0}^{\infty }f(\eta ,\beta |Data)d\beta = \dfrac{\int_{0}^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\beta }{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
where: [math]\displaystyle{ \varphi (\beta )=\frac{1}{\beta } }[/math] is the non-informative prior of β. [math]\displaystyle{ \varphi (\eta )=\frac{1}{\eta } }[/math] is the non-informative prior of η. Using these non-informative prior distributions, [math]\displaystyle{ f(\eta|Data) }[/math] can be rewritten as:
- [math]\displaystyle{ f(\eta |Data)=\dfrac{\int_{0}^{\infty }L(Data|\eta ,\beta )\frac{1}{\beta } \frac{1}{\eta }d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(Data|\eta ,\beta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } }[/math]
The one-sided upper bounds of η is:
- [math]\displaystyle{ CL=P(\eta \leq \eta _{U})=\int_{0}^{\eta _{U}}f(\eta |Data)d\eta }[/math]
The one-sided lower bounds of η is:
- [math]\displaystyle{ 1-CL=P(\eta \leq \eta _{L})=\int_{0}^{\eta _{L}}f(\eta |Data)d\eta }[/math] The two-sided bounds of η is:
- [math]\displaystyle{ CL=P(\eta _{L}\leq \eta \leq \eta _{U})=\int_{\eta _{L}}^{\eta _{U}}f(\eta |Data)d\eta }[/math] Same method is used to obtain the bounds of β.
Bounds on Time (Type 1)
From Chapter 5, we know that:
- [math]\displaystyle{ CL=\Pr (T\leq T_{U})=\Pr (\eta \leq T_{U}\exp (-\frac{\ln (-\ln R)}{\beta })) }[/math] From the posterior distribution of η, we have:
- [math]\displaystyle{ CL=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T_{U}\exp (-\dfrac{ \ln (-\ln R)}{\beta })}L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } EQNREF BayesCLT }[/math]
Eqn. (EQNREF BayesCLT ) is solved numerically for TU. The same method can be applied to calculate one sided lower bounds and two-sided bounds on time.
Bounds on Reliability (Type 2)
- [math]\displaystyle{ CL=\Pr (R\leq R_{U})=\Pr (\eta \leq T\exp (-\frac{\ln (-\ln R_{U})}{\beta })) }[/math] From the posterior distribution of η, we have:
- [math]\displaystyle{ CL=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T\exp (-\dfrac{\ln (-\ln R_{U})}{\beta })}L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } EQNREF BayesCLR }[/math]
Eqn. (EQNREF BayesCLR ) is solved numerically for RU. The same method can be used to calculate the one sided lower bounds and two-sided bounds on reliability.
Weibull-Bayesian Analysis
In this section, the Bayesian methods are presented for the two-parameter Weibull distribution. Bayesian concepts were introduced in Chapter 3. This model considers prior knowledge on the shape (β) parameter of the Weibull distribution when it is chosen to be fitted to a given set of data. There are many practical applications for this model, particularly when dealing with small sample sizes and some prior knowledge for the shape parameter is available. For example, when a test is performed, there is often a good understanding about the behavior of the failure mode under investigation, primarily through historical data. At the same time, most reliability tests are performed on a limited number of samples. Under these conditions, it would be very useful to use this prior knowledge with the goal of making more accurate predictions. A common approach for such scenarios is to use the one-parameter Weibull distribution, but this approach is too deterministic, too absolute you may say (and you would be right). The Weibull-Bayesian model in Weibull++ (which is actually a true "WeiBayes" model, unlike the one-parameter Weibull that is commonly referred to as such) offers an alternative to the one-parameter Weibull, by including the variation and uncertainty that might have been observed in the past on the shape parameter. Applying Bayes's rule on the two-parameter Weibull distribution and assuming the prior distributions of β and η are independent, we obtain the following posterior :
- [math]\displaystyle{ f(\beta ,\eta |Data)=\dfrac{L(\beta ,\eta )\varphi (\beta )\varphi (\eta )}{ \int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math] EQNREF WeibBayes
In this model, η is assumed to follow a noninformative prior distribution with the density function [math]\displaystyle{ \varphi (\eta )=\dfrac{1}{\eta } }[/math]. This is called Jeffrey's prior, and is obtained by performing a logarithmic transformation on η. Specifically, since η is always positive, we can assume that ln(η) follows a uniform distribution, U( − ∞, + ∞). Applying Jeffrey's rule [9] which says "in general, an approximate non-informative prior is taken proportional to the square root of Fisher's information", yields [math]\displaystyle{ \varphi (\eta )=\dfrac{1}{\eta }. }[/math]
The prior distribution of β, denoted as [math]\displaystyle{ \varphi (\beta ) }[/math], can be selected from the following distributions: normal, lognormal, exponential and uniform. The procedure of performing a Weibull-Bayesian analysis is as follows:
- Collect the times-to-failure data.
- Specify a prior distribution for β (the prior for η is assumed to be 1/η).
- Obtain the posterior from Eqn. (EQNREF WeibBayes ).
In other words, a distribution (the posterior ) is obtained, rather than a point estimate as in classical statistics (i.e., as in the parameter estimation methods described previously in this chapter). Therefore, if a point estimate needs to be reported, a point of the posterior needs to be calculated. Typical points of the posterior distribution used are the mean (expected value) or median. In Weibull++, both options are available and can be chosen from the Analysis page, under the Results As area, as shown next.
The expected value of β is obtained by:
- [math]\displaystyle{ E(\beta )=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\beta \cdot f(\beta ,\eta |Data)d\beta d\eta }[/math]
Similarly, the expected value of η is obtained by:
- [math]\displaystyle{ E(\eta )=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\eta \cdot f(\beta ,\eta |Data)d\beta d\eta }[/math]
The median points are obtained by solving the following equations for [math]\displaystyle{ \breve{\beta} }[/math] and [math]\displaystyle{ \breve{\eta} }[/math] respectively:
- [math]\displaystyle{ \int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\breve{\beta}}f(\beta ,\eta |Data)d\beta d\eta =0.5 }[/math]
- and
- [math]\displaystyle{ \int\nolimits_{0}^{\breve{\eta}}\int\nolimits_{0}^{\infty }f(\beta ,\eta |Data)d\beta d\eta =0.5 }[/math]
Of course, other points of the posterior distribution can be calculated as well. For example, one may want to calculate the 10th percentile of the joint posterior distribution (w.r.t. one of the parameters). The procedure for obtaining other points of the posterior distribution is similar to the one for obtaining the median values, where instead of 0.5 the percentage of interest is given. This procedure actually provides the confidence bounds on the parameters, which in the Bayesian framework are called ‘‘Credible Bounds‘‘. However, since the engineering interpretation is the same, and to avoid confusion, we refer to them as confidence bounds in this reference and in Weibull++.
Posterior Distributions for Functions of Parameters
As explained in Chapter 3, in Bayesian analysis, all the functions of the parameters are distributed. In other words, a posterior distribution is obtained for functions such as reliability and failure rate, instead of point estimate as in classical statistics. Therefore, in order to obtain a point estimate for these functions, a point on the posterior distributions needs to be calculated. Again, the expected value (mean) or median value are used.
[math]\displaystyle{ pdf }[/math] of the Times-to-Failure
The posterior distribution of the failure time is given by:
- [math]\displaystyle{ f(T|Data)=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }f(T,\beta ,\eta )f(\beta ,\eta |Data)d\eta d\beta }[/math] EQNREF WeibBayesPDF
- where:
- [math]\displaystyle{ f(T,\beta ,\eta )=\dfrac{\beta }{\eta }\left( \dfrac{T}{\eta }\right) ^{\beta -1}e^{-\left( \dfrac{T}{\eta }\right) ^{\beta }} }[/math]
For the [math]\displaystyle{ pdf }[/math] of the times-to-failure, only the expected value is calculated and reported in Weibull++.
Reliability
In order to calculate the median value of the reliability function, we first need to obtain posterior of the reliability. Since R(T) is a function of β, the density functions of β and R(T) have the following relationship:
- [math]\displaystyle{ \begin{align} f(R|Data,T)dR = & f(\beta |Data)d\beta)\\ = & (\int\nolimits_{0}^{\infty }f(\beta ,\eta |Data)d{\eta}) d{\beta} \\ =& \dfrac{\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }d\beta \end{align} }[/math] EQNREF Rpdf
The median value of the reliability is obtained by solving the following equation w.r.t. [math]\displaystyle{ \breve{R}: }[/math]
- [math]\displaystyle{ \int\nolimits_{0}^{\breve{R}}f(R|Data,T)dR=0.5 }[/math] EQNREF MedRel
The expected value of the reliability at time is given by:
- [math]\displaystyle{ R(T|Data)=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }R(T,\beta ,\eta )f(\beta ,\eta |Data)d\eta d\beta }[/math] where:
- [math]\displaystyle{ R(T,\beta ,\eta )=e^{-\left( \dfrac{T}{\eta }\right) ^{^{\beta }}} }[/math]
Failure Rate
The failure rate at time is given by:
- [math]\displaystyle{ \lambda (T|Data)=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\lambda (T,\beta ,\eta )L(\beta ,\eta )\varphi (\eta )\varphi (\beta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
- where:
- [math]\displaystyle{ \lambda (T,\beta ,\eta )=\dfrac{\beta }{\eta }\left( \dfrac{T}{\eta }\right) ^{\beta -1} }[/math]
Note on Calculated Results
As mentioned above, in order to obtain point estimates for the parameters of functions of the parameters in Bayesian analysis, the Median or Mean values of the different posterior [math]\displaystyle{ pdf }[/math]s are calculated. It is important to note that the Median value is preferable and is the default in Weibull++. This is because the Median value always corresponds to the 50th percentile of the distribution. On the other hand, the Mean is not a fixed point on the distribution, which could cause issues, especially when comparing results across different data sets.
Confidence Bounds on R(T)
The confidence bounds calculation under the Weibull-Bayesian analysis is very similar to the Bayesian Confidence Bounds method described in the previous section, with the exception that in the case of the Weibull-Bayesian Analysis the specified prior of β is considered instead of an non-informative prior. The Bayesian one-sided upper bound estimate for R(T) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{U}(T)}f(R|Data,T)dR=CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and (EQNREF Rpdf ) the following is obtained:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{T\exp (-\dfrac{\ln (-\ln R_{U})}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLRU
Eqn. (EQNREF 1CLRU ) can be solved for RU(T). The Bayesian one-sided lower bound estimate for [math]\displaystyle{ \ R(T) }[/math] is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{L}(T)}f(R|Data,T)dR=1-CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and (EQNREF Rpdf ) the following is obtained:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T\exp (-\dfrac{\ln (-\ln R_{L})}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=1-CL }[/math] EQNREF 1CLRL
Eqn. (EQNREF 1CLRL ) can be solved for RL(T). The Bayesian two-sided bounds estimate for R(T) is given by:
- [math]\displaystyle{ \int\nolimits_{R_{L}(T)}^{R_{U}(T)}f(R|Data,T)dR=CL }[/math] which is equivalent to:
- [math]\displaystyle{ \int\nolimits_{0}^{R_{U}(T)}f(R|Data,T)dR=(1+CL)/2 }[/math]
- and
- [math]\displaystyle{ \int\nolimits_{0}^{R_{L}(T)}f(R|Data,T)dR=(1-CL)/2 }[/math]
Using the same method for one-sided bounds, RU(T)and RL(T) can be computed.
Confidence Bounds on Time [math]\displaystyle{ T }[/math]
Following the same procedure described for bounds on Reliability, the bounds of time can be calculated, given . The Bayesian one-sided upper bound estimate for T(R) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{U}(R)}f(T|Data,R)dT=CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and. (EQNREF WeibBayesPDF ), we obtain:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T_{U}\exp (-\dfrac{\ln (-\ln R)}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLTU
Eqn. (EQNREF 1CLTU ) can be solved for TU(R). The Bayesian one-sided lower bound estimate for T(R) is given by:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{L}(R)}f(T|Data,R)dT=1-CL }[/math]
- or:
- [math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{T_{L}\exp (\dfrac{-\ln (-\ln R)}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLTL
Eqn. (EQNREF 1CLTL ) can be solved for TL(R). The Bayesian two-sided lower bounds estimate for T(R) is:
- [math]\displaystyle{ \int\nolimits_{T_{L}(R)}^{T_{U}(R)}f(T|Data,R)dT=CL }[/math]
which is equivalent to:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{U}(R)}f(T|Data,R)dT=(1+CL)/2 }[/math]
- and:
- [math]\displaystyle{ \int\nolimits_{0}^{T_{L}(R)}f(T|Data,R)dT=(1-CL)/2 }[/math]
Example 6
A manufacturer has tested prototypes of a modified product. The test was terminated at 2000 hours, with only two failures observed from a sample size of eighteen.
| Number of State | State of F or S | State End Time |
|---|---|---|
| 1 | F | 1180 |
| 1 | F | 1842 |
| 16 | S | 2000 |
Because of the lack of failure data in the prototype testing, the manufacturer decided to use information gathered from prior tests on this product to increase the confidence in the results of the prototype testing. This decision was made because failure analysis indicated that the failure mode of these two failures is the same as the one observed in previous tests. In other words, it is expected that the shape of the distribution hasn't changed, but hopefully the scale has, indicating longer life. The two-parameter Weibull distribution have been used to model all prior tests results. The list of the estimated β parameter is as follows:
| Betas Obtained for Similar Mode |
|---|
| 1.7 |
| 2.1 |
| 2.4 |
| 3.1 |
| 3.5 |
First, in order to fit the data to a Weibull-Bayesian model, a prior distribution for β needs to be determined. Based on the prior tests' β values, the prior distribution for β was found to be a lognormal distribution with μ = 0.9064, σ = 0.3325 (obtained by entering the β values into a Weibull++ Standard Folio and analyzing it based on the RRX analysis method.)
the test data is entered into a Standard Folio, the Weibull-Bayesian is selected under Distribution and the β prior distribution is entered after clicking the Calculate button.
Suppose that the reliability at 3000hr is the metric of interest in this example. This reliability can be obtained using Eqn. (EQNREF MedRel ), resulting in the median value of the posterior of the reliability at 3000hr. Using the QCP, this value is calculated to be 76.97. ( By default Weibull++ returns the median values of the posterior distribution. )
The posterior [math]\displaystyle{ pdf }[/math] of the reliability function at 3000hrs can be obtained using Eqn. (EQNREF Rpdf ). In Figure 6-10 the posterior [math]\displaystyle{ pdf }[/math] of the reliability at 3000hrs is plotted, with the corresponding median value as well as the 10th percentile value shown. The 10th percentile constitutes the 90 Lower 1-Sided bound on the reliability at 3000hrs, which is calculated to be 50.77.
Notice that the [math]\displaystyle{ pdf }[/math] plotted in Fig. 6-10 is of the reliability at 3000hrs, and not the [math]\displaystyle{ pdf }[/math] of the times-to-failure data. The [math]\displaystyle{ pdf }[/math] of the times-to-failure data can be obtained using Eqn. (EQNREF WeibBayesPDF ) and plotted using Weibull++, as shown next:
| The material on this page is copyrighted. | ©1992-2012. ReliaSoft Corporation. ALL RIGHTS RESERVED. |

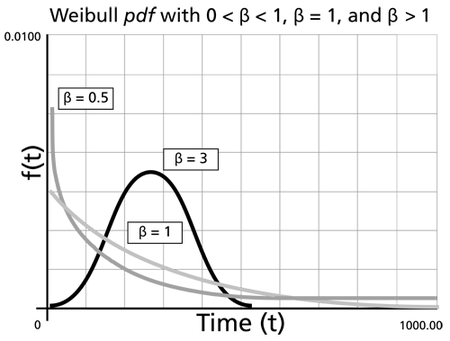
![Effect on [math]\displaystyle{ \beta\,\! }[/math] on the cdf on the Weibull probability plot with a fixed value of [math]\displaystyle{ \eta\,\! }[/math]](/images/b/bf/WB.8_effect_of_weibull.png)
![The effect of values of [math]\displaystyle{ \beta\,\! }[/math] on the Weibull reliability plot.](/images/0/0c/WB.8_weibull_reliability.png)
![The effect of [math]\displaystyle{ \beta\,\! }[/math] on the Weibull failure rate function.](/images/9/9c/WB.8_weibull_failure.png)
![The effects of [math]\displaystyle{ \eta\,\! }[/math] on the Weibull pdf for a common [math]\displaystyle{ \beta\,\! }[/math].](/images/thumb/d/da/WB.8_effects_of_n.png/450px-WB.8_effects_of_n.png)
![The effect of a positive location parameter, [math]\displaystyle{ \gamma\,\! }[/math], on the position of the Weibull pdf.](/images/thumb/8/8b/WB.8_location_parameter.png/450px-WB.8_location_parameter.png)