|
|
| (73 intermediate revisions by 6 users not shown) |
| Line 1: |
Line 1: |
| {{template:ALTABOOK|3}} | | {{template:ALTABOOK|3}} |
| | In this chapter, we will briefly present three lifetime distributions commonly used in accelerated life test analysis: the exponential, the Weibull and the lognormal distributions. Note that although all forms are mentioned below, ALTA uses the 1-parameter form of the exponential distribution and the 2-parameter form of the Weibull distribution. |
|
| |
|
| =Life Distributions=
| | Readers who are interested in a more rigorous overview of these distributions (or for information about other life distributions) can refer to the [https://help.reliasoft.com/reference/life_data_analysis Life data analysis reference]. For information about the parameter estimation methods, see [[Appendix_B:_Parameter_Estimation|Appendix B]].<br> |
| <br> | |
|
| |
|
| In this section we will briefly present three lifetime distributions commonly used in accelerated
| | =The Exponential Distribution= |
| life test analysis, namely the 1-parameter exponential, the 2-parameter Weibull and the lognormal
| | {{Exponential Distribution Definition}} |
| distributions. Readers who are interested in a more rigorous overview or in different forms of
| | ==Exponential Distribution Functions== |
| these and other life distributions can refer to ReliaSoft's Life Data Analysis Reference, Chapters 6-10 [31].
| | {{:Exponential Distribution Functions}} |
| <br>
| | == Characteristics of the Exponential Distribution== |
| | {{:Exponential Distribution Characteristics}} |
|
| |
|
| ==The Exponential Distribution== | | = The Weibull Distribution = |
| <br>
| | {{Weibull Distribution Definition}} |
| | ==Weibull Distribution Functions== |
| | {{:Weibull Distribution Functions}} |
| | ==Characteristics of the Weibull Distribution== |
| | {{:Weibull Distribution Characteristics}} |
|
| |
|
| The exponential distribution is a very commonly used distribution in reliability engineering. Due to its simplicity, it has been widely employed even in cases to which it does not apply. The exponential distribution is used to describe units that have a constant failure rate.
| | = The Lognormal Distribution = |
| The single-parameter exponential <math>pdf</math> is given by:
| | {{Lognormal Distribution Definition}} |
| <br>
| | ==Lognormal Distribution Functions== |
| | | {{:Lognormal Distribution Functions}} |
| ::<math>\begin{align}
| | ==Characteristics of the Lognormal Distribution== |
| & f(T)= & \lambda {{e}^{-\lambda T}}=\frac{1}{m}{{e}^{-\tfrac{1}{m}T}} \\
| | {{:Lognormal Distribution Characteristics}} |
| & T\ge & 0,\lambda >0,m>0
| |
| \end{align}</math>
| |
| <br>
| |
| | |
| where:
| |
| <br>
| |
| • <math>\lambda =</math> constant failure rate, in failures per unit of measurement, e.g. failures per hour, per cycle, etc.
| |
| • <math>\lambda =\tfrac{1}{m}.</math>
| |
| • <math>m=</math> mean time between failures, or to a failure.
| |
| • <math>T=</math> operating time, life, or age, in hours, cycles, miles, actuations, etc.
| |
| <br>
| |
| This distribution requires the estimation of only one parameter, <math>\lambda </math> , for its application.
| |
|
| |
| <br>
| |
| | |
| ===Statistical Properties Summary===
| |
| <br>
| |
| | |
| ====The Mean or MTTF====
| |
| <br>
| |
| | |
| The mean, <math>\overline{T},</math> or Mean Time To Failure (MTTF) of the 1-parameter exponential distribution is given by:
| |
| <br>
| |
| | |
| ::<math>\begin{align}
| |
| & \overline{T}= & \mathop{}_{0}^{\infty }t\cdot f(t)dt=\mathop{}_{0}^{\infty }t\cdot \lambda \cdot {{e}^{-\lambda t}}dt \\
| |
| & = & \frac{1}{\lambda }
| |
| \end{align}</math>
| |
| | |
| ====The Median====
| |
| | |
| <br>
| |
| The median, <math>\breve{T}</math>,
| |
| of the 1-parameter exponential distribution is given by:
| |
| <br>
| |
| ::<math>\breve{T}=\frac{1}{\lambda }0.693</math>
| |
| | |
| <br>
| |
| | |
| ====The Mode====
| |
| <br>
| |
| The mode, <math>\tilde{T},</math>
| |
| of the 1-parameter exponential distribution is given by:
| |
| <br>
| |
| | |
| ::<math>\tilde{T}=0</math>
| |
| | |
| <br>
| |
| | |
| ====The Standard Deviation====
| |
| <br>
| |
| The standard deviation, <math>{{\sigma }_{T}}</math> , of the 1-parameter exponential distribution is given by:
| |
| | |
| <br>
| |
| ::<math>{{\sigma }_{T}}=\frac{1}{\lambda }=m</math>
| |
| | |
| <br>
| |
| ====The Reliability Function====
| |
| | |
| <br>
| |
| The 1-parameter exponential reliability function is given by:
| |
| | |
| <br>
| |
| ::<math>R(T)={{e}^{-\lambda T}}={{e}^{-\tfrac{T}{m}}}</math>
| |
| <br>
| |
| This function is the complement of the exponential cumulative distribution function or:
| |
| | |
| <br>
| |
| ::<math>R(T)=1-Q(T)=1-\mathop{}_{0}^{T}f(T)dT</math>
| |
| | |
| <br>
| |
| and:
| |
| | |
| <br>
| |
| ::<math>R(T)=1-\mathop{}_{0}^{T}\lambda {{e}^{-\lambda T}}dT={{e}^{-\lambda T}}</math>
| |
| | |
| | |
| <br>
| |
| ====Conditional Reliability====
| |
| <br>
| |
| The conditional reliability function for the 1-parameter exponential distribution is given by:
| |
| | |
| <br>
| |
| ::<math>R(T,t)=\frac{R(T+t)}{R(T)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\lambda t}}</math>
| |
| <br>
| |
| which says that the reliability for a mission of <math>t</math> duration undertaken after the component or equipment has already accumulated <math>T</math> hours of operation from age zero is only a function of the mission duration, and not a function of the age at the beginning of the mission. This is referred to as the ``memoryless property.''
| |
| <br>
| |
| ====Reliable Life====
| |
| <br>
| |
| The reliable life, or the mission duration for a desired reliability goal, <math>{{t}_{R}}</math> , for the 1-parameter exponential distribution is given by:
| |
| <br>
| |
| | |
| ::<math>\begin{align}
| |
| & R({{t}_{R}})= & {{e}^{-\lambda {{t}_{R}}}} \\
| |
| & & \\
| |
| & \ln [R({{t}_{R}})]= & -\lambda {{t}_{R}}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| or:
| |
| <br>
| |
| | |
| ::<math>{{t}_{R}}=-\frac{\ln [R({{t}_{R}})]}{\lambda }</math>
| |
| | |
| <br>
| |
| ====Failure Rate Function====
| |
| | |
| <br>
| |
| The exponential failure rate function is given by:
| |
| | |
| <br>
| |
| ::<math>\lambda (T)=\frac{f(T)}{R(T)}=\frac{\lambda {{e}^{-\lambda (T)}}}{{{e}^{-\lambda (T)}}}=\lambda =\text{Constant}</math>
| |
| | |
| <br>
| |
| ===Characteristics===
| |
| | |
| <br>
| |
| The characteristics of the 1-parameter exponential distribution can be exemplified by examining its parameter, lambda, <math>\lambda ,</math> and the effect lambda has on the <math>pdf</math> , reliability and failure rate functions.
| |
| <br>
| |
| ====Effects of <math>\lambda </math> on the pdf====
| |
| <br>
| |
| [[File:ALTA4pdf.gif|center]]
| |
| <br>
| |
| ::Fig. 1: ''Pdf'' plot of the exponential distribution.
| |
| <br>
| |
| | |
| ::<math></math>
| |
| <br>
| |
| | |
| • The scale parameter is <math>\tfrac{1}{\lambda }</math> .
| |
| • As <math>\lambda </math> is decreased in value, the distribution is stretched out to the right, and as <math>\lambda </math> is increased, the distribution is pushed toward the origin.
| |
| • This distribution has no shape parameter as it has only one shape, i.e. the exponential. The only parameter it has is the failure rate, <math>\lambda </math> .
| |
| • The distribution starts at <math>T=0</math> at the level of <math>f(T=0)=\lambda </math> and decreases thereafter exponentially and monotonically as <math>T</math> increases, and is convex.
| |
| • As <math>T\to \infty </math> , <math>f(T)\to 0</math>.
| |
| • This <math>pdf</math> can be thought of as a special case of the Weibull <math>pdf</math> with <math>\beta =1</math> .
| |
| <br>
| |
| [[File:ALTA4reliabilityvstimeplot.gif|center]]
| |
| <br>
| |
| ::Fig. 2: Reliability plot of the exponential distributution.
| |
| <br>
| |
| | |
| ====Effects of <math>\lambda </math> on the Reliability Function====
| |
| | |
| <br>
| |
| • The 1-parameter exponential reliability function starts at the value of 1 at <math>T=0</math> . It decreases thereafter monotonically and is convex.
| |
| • As <math>T\to \infty </math> , <math>R(T\to \infty )\to 0</math>.
| |
| Effects of <math>\lambda </math> on the Failure Rate Function
| |
| The failure rate function for the exponential distribution is constant and it is equal to the parameter <math>\lambda </math> .
| |
| <br>
| |
| [[File:ALTA4FRvsTP.gif|center]]
| |
| <br>
| |
| ::Fig. 3:Failure Rate plot of the exponential distribution.
| |
| <br>
| |
| | |
| ==Parameter Estimation==
| |
| The parameter of the exponential distribution can be estimated graphically on probability plotting paper or analytically using either least squares or maximum likelihood. (Parameter estimation methods are presented in detail in Appendix B.)
| |
| | |
| ==Probability Plotting==
| |
| One method of calculating the parameter of the exponential distribution is by using probability plotting. To better illustrate this procedure, consider the following example.
| |
| | |
| <br>
| |
| | |
| ====Example 1====
| |
| <br>
| |
| | |
| Let's assume six identical units are reliability tested at the same application and operation
| |
| stress levels. All of these units fail during the test after operating for the following times (in hours), <math>{{T}_{i}}</math> : 96, 257, 498, 763, 1051 and 1744.
| |
| <br>
| |
| The steps for determining the parameters of the exponential <math>pdf</math> representing the
| |
| data, using probability plotting, are as follows:
| |
| <br>
| |
| • Rank the times-to-failure in ascending order as shown next.
| |
| <br>
| |
| | |
| ::<math>\begin{matrix}
| |
| \text{Time-to-} & \text{Failure Order Number} \\
| |
| \text{failure, hr} & \text{out of a Sample Size of 6} \\
| |
| \text{96} & \text{1} \\
| |
| \text{257} & \text{2} \\
| |
| \text{498} & \text{3} \\
| |
| \text{763} & \text{4} \\
| |
| \text{1,051} & \text{5} \\
| |
| \text{1,744} & \text{6} \\
| |
| \end{matrix}</math>
| |
| | |
| <br>
| |
| • Obtain their median rank plotting positions.
| |
| <br>
| |
| Median rank positions are used instead of other ranking methods because median ranks are at a
| |
| specific confidence level (50%).
| |
| <br>
| |
| • The times-to-failure, with their corresponding median ranks, are shown next:
| |
| | |
| <br>
| |
| ::<math>\begin{matrix}
| |
| \text{Time-to-} & \text{Median} \\
| |
| \text{failure, hr} & \text{Rank, }% \\
| |
| \text{96} & \text{10}\text{.91} \\
| |
| \text{257} & \text{26}\text{.44} \\
| |
| \text{498} & \text{42}\text{.14} \\
| |
| \text{763} & \text{57}\text{.86} \\
| |
| \text{1,051} & \text{73}\text{.56} \\
| |
| \text{1,744} & \text{89}\text{.10} \\
| |
| \end{matrix}</math>
| |
| | |
| <br>
| |
| • On an exponential probability paper, plot the times on the x-axis and their corresponding
| |
| rank value on the y-axis. Fig. 4 displays an example of an exponential probability paper. The
| |
| paper is simply a log-linear paper. (The solution is given in Fig. 2.)
| |
| <br>
| |
| [[File:ALTA4.1.gif|center]]
| |
| <br>
| |
| ::Fig. 4: Sample exponential probability paper.
| |
| <br>
| |
| • Draw the best possible straight line that goes through the <math>t=0</math> and <math>
| |
| (t)=100%</math> point and through the plotted points (as shown in Fig. 5).
| |
| <br>
| |
| • At the <math>Q(t)=63.2%</math> or <math>R(t)=36.8%</math> ordinate point, draw a
| |
| straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of the mean. For this case, <math>\widehat{\mu }=833</math> hr which means that <math>\lambda =\tfrac{1}{\mu }=0.0012</math> . (This is always at 63.2% since <math>(T)=1-{{e}^{-\tfrac{\mu }{\mu }}}=1-{{e}^{-1}}=0.632=63.2%).</math>
| |
| <br>
| |
| [[File:ALTA4.2.gif|center]]
| |
| <br>
| |
| ::Fig. 5: Probability plot for Example 1.
| |
| <br>
| |
| <br>
| |
| Now any reliability value for any mission time <math>t</math> can be obtained. For example, the
| |
| reliability for a mission of 15 hr, or any other time, can now be obtained either from the plot or analytically (i.e. using the equations given in Section <math>5.1.1</math> ).
| |
| | |
| <br>
| |
| To obtain the value from the plot, draw a vertical line from the abscissa, at <math>t=15</math>
| |
| hr, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read
| |
| <math>R(t)</math> . In this case, <math>R(t=15)=98.15%</math> . This can also be obtained
| |
| analytically, from the exponential reliability function.
| |
| | |
| <br>
| |
| | |
| ====MLE Parameter Estimation====
| |
| | |
| <br>
| |
| The parameter of the exponential distribution can also be estimated using the maximum likelihood estimation (MLE) method. This log-likelihood function is:
| |
| | |
| <br>
| |
| ::<math>\ln (L)=\Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }]</math>
| |
| <br>
| |
| where:
| |
| <br>
| |
| ::<math>R_{Li}^{\prime \prime }={{e}^{-\lambda T_{Li}^{\prime \prime }}}</math>
| |
| | |
| <br>
| |
| ::<math>R_{Ri}^{\prime \prime }={{e}^{-\lambda T_{Ri}^{\prime \prime }}}</math>
| |
| | |
| <br>
| |
| and:
| |
| <br>
| |
| • <math>{{F}_{e}}</math> is the number of groups of times-to-failure data points.
| |
| <br>
| |
| • <math>{{N}_{i}}</math> is the number of times-to-failure in the <math>{{i}^{th}}</math> time-to-failure data group.
| |
| <br>
| |
| • <math>\lambda </math> is the failure rate parameter (unknown a priori, the only parameter to be found).
| |
| <br>
| |
| • <math>{{T}_{i}}</math> is the time of the <math>{{i}^{th}}</math> group of time-to-failure data.
| |
| <br>
| |
| • <math>S</math> is the number of groups of suspension data points.
| |
| <br>
| |
| • <math>N_{i}^{\prime }</math> is the number of suspensions in the <math>{{i}^{th}}</math> group of suspension data points.
| |
| <br>
| |
| • <math>T_{i}^{\prime }</math> is the time of the <math>{{i}^{th}}</math> suspension data group.
| |
| <br>
| |
| • <math>FI</math> is the number of interval data groups.
| |
| <br>
| |
| • <math>N_{i}^{\prime \prime }</math> is the number of intervals in the i <math>^{th}</math> group of data intervals.
| |
| <br>
| |
| • <math>T_{Li}^{\prime \prime }</math> is the beginning of the i <math>^{th}</math> interval.
| |
| <br>
| |
| • <math>T_{Ri}^{\prime \prime }</math> is the ending of the i <math>^{th}</math> interval.
| |
| <br>
| |
| <br>
| |
| The solution will be found by solving for a parameter <math>\widehat{\lambda }</math> so that <math>\tfrac{\partial \Lambda }{\partial \lambda }=0</math> where:
| |
| <br>
| |
| ::<math>\frac{\partial \Lambda }{\partial \lambda }=\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{1}{\lambda }-{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }T_{i}^{\prime }-\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }}</math>
| |
| | |
| <br>
| |
| | |
| ====Example 2====
| |
| | |
| <br>
| |
| Using the same data as in the probability plotting example (Example 1), and assuming an exponential distribution, estimate the parameter using the MLE method.
| |
| <br>
| |
| ''Solution''
| |
| <br>
| |
| In this example we have non-grouped data without suspensions. Thus Eqn. (exp-mle) becomes:
| |
| <br>
| |
| ::<math>\frac{\partial \Lambda }{\partial \lambda }=\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,\left[ \frac{1}{\lambda }-\left( {{T}_{i}} \right) \right]=\underset{i=1}{\overset{14}{\mathop \sum }}\,\left[ \frac{1}{\lambda }-\left( {{T}_{i}} \right) \right]=0</math>
| |
| | |
| <br>
| |
| Substituting the values for <math>T</math> we get:
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \frac{6}{\lambda }= & 4409,\text{ or:} \\
| |
| & \lambda = & 0.00136\text{ failure/hr}
| |
| \end{align}</math>
| |
| | |
| ==The Weibull Distribution==
| |
| <br>
| |
| The Weibull distribution is one of the most commonly used distributions in reliability engineering because of the many shapes it attains for various values of <math>\beta </math> (slope). It can therefore model a great variety of data and life characteristics [18].
| |
| | |
| <br>
| |
| The 2-parameter Weibull <math>pdf</math> is given by:
| |
| <br>
| |
| ::<math>f(T)=\frac{\beta }{\eta }{{\left( \frac{T}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}</math>
| |
| <br>
| |
| where:
| |
| | |
| <br>
| |
| ::<math>f(T)\ge 0,\text{ }T\ge 0,\text{ }\beta >0,\text{ }\eta >0\text{ }</math>
| |
| <br>
| |
| and:
| |
| <br>
| |
| • <math>\eta =</math> scale parameter.
| |
| • <math>\beta =</math> shape parameter (or slope).
| |
| | |
| <br>
| |
| ===Statistical Properties Summary===
| |
| <br>
| |
| | |
| ====The Mean or MTTF====
| |
| <br>
| |
| | |
| The mean, <math>\overline{T},</math> of the 2-parameter Weibull <math>pdf</math> is given by:
| |
| <br>
| |
| | |
| ::<math>\overline{T}=\eta \cdot \Gamma \left( \frac{1}{\beta }+1 \right)</math>
| |
| | |
| <br>
| |
| where <math>\Gamma \left( \tfrac{1}{\beta }+1 \right)</math> is the gamma function evaluated at the value of <math>\left( \tfrac{1}{\beta }+1 \right)</math> .
| |
| | |
| <br>
| |
| ====The Median====
| |
| | |
| <br>
| |
| The median, <math>\breve{T},</math>
| |
| of the 2-parameter Weibull is given by:
| |
| <br>
| |
| ::<math>\breve{T}=\eta {{\left( \ln 2 \right)}^{\tfrac{1}{\beta }}}</math>
| |
| | |
| <br>
| |
| | |
| ====The Mode====
| |
| | |
| <br>
| |
| The mode, <math>\tilde{T},</math>
| |
| of the 2-parameter Weibull is given by:
| |
| | |
| <br>
| |
| ::<math>\tilde{T}=\eta {{\left( 1-\frac{1}{\beta } \right)}^{\tfrac{1}{\beta }}}</math>
| |
| | |
| <br>
| |
| | |
| ====The Standard Deviation====
| |
| | |
| The standard deviation, <math>{{\sigma }_{T}},</math>
| |
| of the 2-parameter Weibull is given by:
| |
| | |
| | |
| ::<math>{{\sigma }_{T}}=\eta \cdot \sqrt{\Gamma \left( \frac{2}{\beta }+1 \right)-\Gamma {{\left( \frac{1}{\beta }+1 \right)}^{2}}}</math>
| |
| | |
| ====The <math>cdf</math> and the Reliability Function====
| |
| | |
| The <math>cdf</math> of the 2-parameter Weibull distribution is given by:
| |
| | |
| | |
| ::<math>F(T)=1-{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}</math>
| |
| | |
| | |
| The Weibull reliability function is given by:
| |
| | |
| ::<math>\begin{align}
| |
| & R(T)= & 1-F(t) \\
| |
| & = & {{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}
| |
| \end{align}</math>
| |
| | |
| ====The Conditional Reliability Function====
| |
| | |
| The Weibull conditional reliability function is given by:
| |
| | |
| <math>R(T,t)=\frac{R(T+t)}{R(T)}=\frac{{{e}^{-{{\left( \tfrac{T+t}{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}}</math>
| |
| | |
| | |
| or:
| |
| | |
| <math>R(T,t)={{e}^{-\left[ {{\left( \tfrac{T+t}{\eta } \right)}^{\beta }}-{{\left( \tfrac{T}{\eta } \right)}^{\beta }} \right]}}</math>
| |
| | |
| | |
| Eqn. (e137) gives the reliability for a new mission of <math>t</math> duration, having already accumulated <math>T</math> hours of operation up to the start of this new mission, and the units are checked out to assure that they will start the next mission successfully. (It is called conditional because you can calculate the reliability of a new mission based on the fact that the unit(s) already accumulated <math>T</math> hours of operation successfully.)
| |
| | |
| ====The Reliable Life====
| |
| | |
| For the 2-parameter Weibull distribution, the reliable life, <math>{{T}_{R}}</math> , of a unit for a specified reliability, starting the mission at age zero, is given by:
| |
| | |
| ::<math>{{T}_{R}}=\eta \cdot {{\left\{ -\ln \left[ R\left( {{T}_{R}} \right) \right] \right\}}^{\tfrac{1}{\beta }}}</math>
| |
| | |
| | |
| This is the life for which the unit will function successfully with a reliability of <math>R({{T}_{R}})</math> . If <math>R({{T}_{R}})=0.50</math> then <math>{{T}_{R}}=\breve{T}</math>,
| |
| the median life, or the life by which half of the units will survive.
| |
| <br>
| |
| | |
| ====The Failure Rate Function====
| |
| <br>
| |
| The 2-parameter Weibull failure rate function,<math>\lambda (T)</math> ,
| |
| is given by:
| |
| | |
| ::<math>\lambda \left( T \right)=\frac{f\left( T \right)}{R\left( T \right)}=\frac{\beta }{\eta }{{\left( \frac{T}{\eta } \right)}^{\beta -1}}</math>
| |
| | |
| | |
| ===Characteristics===
| |
| | |
| The characteristics of the 2-parameter Weibull distribution can be exemplified by examining the two parameters, beta, <math>\beta ,</math> and eta, <math>\eta ,</math> and the effect they have on the <math>pdf,</math> reliability and failure rate functions.
| |
| | |
| ====Looking at <math>\beta </math>====
| |
| | |
| <br>
| |
| Beta, <math>\beta ,</math> is called the shape parameter or slope of the Weibull distribution. Changing the value of <math>\beta </math> forces a change in the shape of the <math>pdf</math> as shown in Fig. 6. In addition, when the <math>cdf</math> is plotted on Weibull probability paper, as shown in Fig. 7, a change in beta is a change in the slope of the distribution on Weibull probability paper.
| |
| <br>
| |
| '''Effects of <math>\beta </math> on the ''pdf'''''
| |
| <br>
| |
| <br>
| |
| [[File:ALTA4.3.gif|center]]
| |
| <br>
| |
| ::Fig. 6: Weibull ''pdf'' with <math>0<\Beta<1</math>, <math>\Beta=1 </math> and a fixed <math>\eta </math>.
| |
| | |
| <br>
| |
| | |
| | |
| <br>
| |
| ::<math></math>
| |
| | |
| <br>
| |
| <br>
| |
| • For <math>0<\beta <1</math> , the failure rate decreases with time and:
| |
| ::o As <math>T\to 0,</math> <math>f(T)\to \infty .</math>
| |
| ::o As <math>T\to \infty </math> , <math>f(T)\to 0</math> .
| |
| ::o <math>f(T)</math> decreases monotonically and is convex as <math>T</math> increases.
| |
| ::o The mode is non-existent.
| |
| <br>
| |
| <br>
| |
| • For <math>\beta =1,</math> it becomes the exponential distribution, as a special case, <br>
| |
| <br>
| |
| or:
| |
| <br>
| |
| <br>
| |
| ::<math>f(T)=\frac{1}{\eta }{{e}^{-\tfrac{T}{\eta }}};\text{ }\eta >0,T\ge 0</math>
| |
| <br>
| |
| where <math>\tfrac{1}{\eta }=\lambda =</math> chance, useful life, or failure rate.
| |
| <br>
| |
| <br>
| |
| • For <math>\beta >1</math> , <math>f(T),</math> the Weibull assumes wear-out type shapes (i.e. the failure rate increases with time) and:
| |
| <br>
| |
| ::o <math>f(T)=0</math> at <math>T=0</math> .
| |
| ::o <math>f(T)</math> increases as <math>T\to \tilde{T}</math> (mode) and decreases thereafter.
| |
| ::o For <math>\beta =2</math> it becomes the Rayleigh distribution as a special case. For <math>\beta <2.6</math> the Weibull <math>pdf</math> is positively skewed (has a right tail), for <math>2.6<\beta <3.7</math> its coefficient of skewness approaches zero (no tail); consequently, it may approximate the normal <math>pdf</math> , and for <math>\beta >3.7</math> it is negatively skewed (left tail).
| |
| <br>
| |
| <br>
| |
| • The parameter <math>\beta </math> is a pure number, i.e. it is dimensionless.
| |
| | |
| <br>
| |
| '''Effects of <math>\beta </math> on the Reliability Function and the ''cdf'''''
| |
| <br>
| |
| [[File:ALTA4.4.gif|center]]
| |
| <br>
| |
| ::Fig. 7: Weibull ''cdf'', or Unreliability vs. Time, on Weibull probability plotting paper with <math>0<\Beta<1</math>, <math>\Beta=1 </math> and a fixed <math>\eta </math>.
| |
| <br>
| |
| [[File:ALTA4.5.gif|center]]
| |
| <br>
| |
| ::Fig. 8: Weibull 1-''cdf'', or Reliability vs. Time, on linear scales with <math>0<\Beta<1</math>, <math>\Beta=1 </math> and a fixed <math>\eta </math>.
| |
| | |
| <br>
| |
| | |
| ::<math></math>
| |
| | |
| <br>
| |
| <br>
| |
| • <math>R(T)</math> decreases sharply and monotonically for <math>0<\beta <1</math> , it is convex, and decreases less sharply for the same <math>\beta </math> .
| |
| <br>
| |
| <br>
| |
| • For <math>\beta =1</math> and the same <math>\eta </math> , <math>R(T)</math> decreases monotonically but less sharply than for <math>0<\beta <1</math> , and is convex.
| |
| <br>
| |
| <br>
| |
| • For <math>\beta >1</math> , <math>R(T)</math> decreases as <math>T</math> increases but less sharply than before, and as wear-out sets in, it decreases sharply and goes through an inflection point.
| |
| <br>
| |
|
| |
| '''Effects of <math>\beta </math> on the Failure Rate Function'''
| |
| <br>
| |
| [[File:ALTA4.6.gif|center]]
| |
| <br>
| |
| ::Fig. 9: Weibull Failure Rate vs. Time with <math>0<\Beta<1 </math>, <math>\Beta=1 </math>, <math>\Beta>1 </math> .
| |
| | |
| | |
| <br>
| |
| ::<math></math>
| |
| | |
| <br>
| |
| <br>
| |
| • The Weibull failure rate for <math>0<\beta <1</math> is unbounded at <math>T=0</math> . The failure rate, <math>\lambda (T),</math> decreases thereafter monotonically and is convex, approaching the value of zero as <math>T\to \infty </math> or <math>\lambda (\infty )=0</math> . This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When such behavior is encountered, one or more of the following conclusions can be drawn:
| |
| <br>
| |
| ::o Burn-in testing and/or environmental stress screening are not well implemented.
| |
| ::o There are problems in the production line.
| |
| ::o Inadequate quality control.
| |
| ::o Packaging and transit problems.
| |
| <br>
| |
| • For <math>\beta =1</math> , <math>\lambda (T)</math> yields a constant value of <math>\tfrac{1}{\eta }</math> , or:
| |
|
| |
| <br>
| |
| ::<math>\lambda (T)=\lambda =\frac{1}{\eta }</math>
| |
|
| |
| <br>
| |
| This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
| |
| <br>
| |
| <br>
| |
| • For <math>\beta >1</math> , <math>\lambda (T)</math> increases as <math>T</math> increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For <math>1<\beta <2</math> the <math>\lambda (T)</math> curve is concave, consequently the failure rate increases at a decreasing rate as <math>T</math> increases.
| |
| <br>
| |
| <br>
| |
| • For <math>\beta =2</math> , or for the Rayleigh distribution case, the failure rate function is given by:
| |
|
| |
| <br>
| |
| ::<math>\lambda (T)=\frac{2}{\eta }\left( \frac{T}{\eta } \right)</math>
| |
|
| |
| <br>
| |
| hence there emerges a straight line relationship between <math>\lambda (T)</math> and <math>T</math> , starting at a value of <math>\lambda (T)=0</math> at <math>T=0</math> , and increasing thereafter with a slope of <math>\tfrac{2}{{{\eta }^{2}}}</math> . Consequently, the failure rate increases at a constant rate as <math>T</math> increases. Furthermore, if <math>\eta =1</math> the slope becomes equal to 2, and <math>\lambda (T)</math> becomes a straight line which passes through the origin with a slope of 2.
| |
| <br>
| |
| <br>
| |
| • When <math>\beta >2</math> the <math>\lambda (T)</math> curve is convex, with its slope increasing as <math>T</math> increases. Consequently, the failure rate increases at an increasing rate as <math>T</math> increases, indicating wear-out life.
| |
| | |
| <br>
| |
| <br>
| |
| | |
| ====Looking at <math>\eta </math>====
| |
| | |
| | |
| Eta, <math>\eta ,</math> is called the scale parameter of the Weibull distribution. The parameter <math>\eta </math> has the same units as <math>T</math> , such as hours, miles, cycles, actuations, etc.
| |
| <br>
| |
| [[File:ALTA4.7.gif|center]]
| |
| <br>
| |
|
| |
| <br>
| |
| • A change in the scale parameter <math>\eta </math> has the same effect on the distribution as a change of the abscissa scale.
| |
| ::o If <math>\eta </math> is increased while <math>\beta </math> is kept the same, the distribution gets stretched out to the right and its height decreases, while maintaining its shape and location.
| |
| ::o If <math>\eta </math> is decreased while <math>\beta </math> is kept the same, the distribution gets pushed in toward the left (i.e. toward its beginning, or 0) and its height increases.
| |
| <br>
| |
| | |
| ===Parameter Estimation===
| |
| | |
| <br>
| |
| The estimates of the parameters of the Weibull distribution can be found graphically on probability plotting paper, or analytically using either least squares or maximum likelihood. (Parameter estimation methods are presented in detail in Appendix B.)
| |
| <br>
| |
| ====Probability Plotting====
| |
| <br>
| |
| One method of calculating the parameters of the Weibull distribution is by using probability plotting. To better illustrate this procedure, consider the following example [18].
| |
| | |
| <br>
| |
| ====Example 3====
| |
| | |
| <br>
| |
| Let's assume six identical units are being reliability tested at the same application and operation stress levels. All of these units fail during the test after operating the following times (in hours), <math>{{T}_{i}}</math> : 93, 34, 16, 120, 53 and 75.
| |
| The steps for determining the parameters of the Weibull <math>pdf</math> representing the data, using probability plotting, are as follows:
| |
| <br>
| |
| • Rank the times-to-failure in ascending order as shown next.
| |
| | |
| <br>
| |
| ::<math>\begin{matrix}
| |
| \text{Time-to-} & \text{Failure Order Number} \\
| |
| \text{failure, hrs} & \text{out of a Sample Size of 6} \\
| |
| \text{16} & \text{1} \\
| |
| \text{34} & \text{2} \\
| |
| \text{53} & \text{3} \\
| |
| \text{75} & \text{4} \\
| |
| \text{93} & \text{5} \\
| |
| \text{120} & \text{6} \\
| |
| \end{matrix}</math>
| |
|
| |
| <br>
| |
| • Obtain their median rank plotting positions. The times-to-failure, with their corresponding median ranks, are shown next.
| |
| | |
| <br>
| |
| ::<math>\begin{matrix}
| |
| \text{Time-to-} & \text{Median} \\
| |
| \text{failure, hr} & \text{Rank, }% \\
| |
| \text{16} & \text{10}\text{.91} \\
| |
| \text{34} & \text{26}\text{.44} \\
| |
| \text{53} & \text{42}\text{.14} \\
| |
| \text{75} & \text{57}\text{.86} \\
| |
| \text{93} & \text{73}\text{.56} \\
| |
| \text{120} & \text{89}\text{.10} \\
| |
| \end{matrix}</math>
| |
| | |
| <br>
| |
| • On a Weibull probability paper, plot the times and their corresponding ranks. Fig. 11 displays an example of a Weibull probability paper (the solution is given in Fig. 12).
| |
| <br>
| |
| [[File:ALTA4.8.gif|center]]
| |
| <br>
| |
| ::Fig.11: Sample Weibull probability paper.
| |
| <br>
| |
| <br>
| |
| • Draw the best possible straight line through the plotted points (as shown in Fig. 12).
| |
| <br>
| |
| • Obtain the slope of this line by drawing a line, parallel to the one just obtained, through the slope indicator. This value is the estimate of the shape parameter <math>\widehat{\beta }</math> . In this case <math>\widehat{\beta }=1.4</math> .
| |
| <br>
| |
| • At the <math>Q(t)=63.2%</math> ordinate point, draw a straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of <math>\widehat{\eta }</math> . For this case <math>\widehat{\eta }=76</math> hr. (This is always at 63.2% since <math>Q(T)=1-{{e}^{-{{(\tfrac{\eta }{\eta })}^{\beta }}}}=1-{{e}^{-1}}=0.632=63.2%).</math>
| |
| <br>
| |
| [[File:ALTA4.9.gif|center]]
| |
| <br>
| |
| ::Fig. 12: Probability plot for Example 3.
| |
| <br>
| |
| | |
| Now any reliability value for any mission time <math>t</math> can be obtained. For example, the reliability for a mission of 15 hr, or any other time, can now be obtained either from the plot or analytically (i.e. using the equations given in Section 5.2.1).
| |
| To obtain the value from the plot, draw a vertical line from the abscissa, at <math>t=15</math> hr, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read <math>Q(t)</math> , in this case <math>Q(t=15)=9.8%</math> . Thus, <math>R(t=15)=1-Q(t)=90.2%</math> . This can also be obtained analytically from the Weibull reliability function since both of the parameters are known.
| |
| <br>
| |
| ::<math>R(t=15)={{e}^{-{{\left( \tfrac{15}{\eta } \right)}^{\beta }}}}={{e}^{-{{\left( \tfrac{15}{76} \right)}^{1.4}}}}=90.2%.</math>
| |
| <br>
| |
| <br>
| |
| <br>
| |
| | |
| ==MLE Parameter Estimation==
| |
| | |
| <br>
| |
| The parameters of the 2-parameter Weibull distribution can also be estimated using Maximum Likelihood Estimation (MLE). This log-likelihood function is composed of :
| |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{{{T}_{i}}}{\eta } \right)}^{\beta }}}} \right] \\
| |
| & & -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }}\overset{FI}{\mathop{+\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }]
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| where:
| |
| | |
| | |
| | |
| <br>
| |
| ::<math>R_{Li}^{\prime \prime }={{e}^{-{{(\tfrac{T_{Li}^{\prime \prime }}{\eta })}^{\beta }}}}</math>
| |
| | |
|
| |
| | |
| <br>
| |
| ::<math>R_{Ri}^{\prime \prime }={{e}^{-{{(\tfrac{T_{Ri}^{\prime \prime }}{\eta })}^{\beta }}}}</math>
| |
| | |
| | |
| <br>
| |
| • <math>{{F}_{e}}</math> is the number of groups of times-to-failure data points.
| |
| <br>
| |
| • .. is the number of times-to-failure in the <math>{{i}^{th}}</math> time-to-failure data group.
| |
| <br>
| |
| • <math>\beta </math> is the Weibull shape parameter (unknown a priori, the first of two parameters to be found).
| |
| <br>
| |
| • <math>\eta </math> is the Weibull scale parameter (unknown a priori, the second of two parameters to be found).
| |
| <br>
| |
| • <math>{{T}_{i}}</math> is the time of the <math>{{i}^{th}}</math> group of time-to-failure data.
| |
| <br>
| |
| • <math>S</math> is the number of groups of suspension data points.
| |
| <br>
| |
| • <math>N_{i}^{\prime }</math> is the number of suspensions in <math>{{i}^{th}}</math> group of suspension data points.
| |
| <br>
| |
| • <math>T_{i}^{\prime }</math> is the time of the <math>{{i}^{th}}</math> suspension data group.
| |
| <br>
| |
| • <math>FI</math> is the number of interval data groups.
| |
| <br>
| |
| • <math>N_{i}^{\prime \prime }</math> is the number of intervals in the i <math>^{th}</math> group of data intervals.
| |
| <br>
| |
| • <math>T_{Li}^{\prime \prime }</math> is the beginning of the i <math>^{th}</math> interval.
| |
| <br>
| |
| • <math>T_{Ri}^{\prime \prime }</math> is the ending of the i <math>^{th}</math> interval.
| |
| <br>
| |
| <br>
| |
| The solution is found by solving for a pair of parameters <math>\left( \widehat{\beta },\widehat{\eta } \right)</math> so that <math>\tfrac{\partial \Lambda }{\partial \beta }=0</math> and <math>\tfrac{\partial \Lambda }{\partial \eta }=0.</math> (Other methods can also be used, such as direct maximization of the likelihood function, without having to compute the derivatives.)
| |
| | |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \frac{\partial \Lambda }{\partial \beta }= & \frac{1}{\beta }\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}+\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}\ln \left( \frac{{{T}_{i}}}{\eta } \right) \\
| |
| & & -\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta }}\ln \left( \frac{{{T}_{i}}}{\eta } \right)-\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }}\ln \left( \frac{T_{i}^{\prime }}{\eta } \right) \\
| |
| & & +\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{-{{(\tfrac{T_{Li}^{\prime \prime }}{\eta })}^{\beta }}\ln (\tfrac{T_{Li}^{\prime \prime }}{\eta })R_{Li}^{\prime \prime }+{{(\tfrac{T_{Ri}^{\prime \prime }}{\eta })}^{\beta }}\ln (\tfrac{T_{Ri}^{\prime \prime }}{\eta })R_{Ri}^{\prime \prime }}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \\
| |
| & & \\
| |
| & \frac{\partial \Lambda }{\partial \eta }= & \frac{-\beta }{\eta }\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}+\frac{\beta }{\eta }\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta }} \\
| |
| & & +\frac{\beta }{\eta }\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\beta }{\eta }\frac{{{(\tfrac{T_{Li}^{\prime \prime }}{\eta })}^{\beta }}R_{Li}^{\prime \prime }-{{(\tfrac{T_{Ri}^{\prime \prime }}{\eta })}^{\beta }}R_{Ri}^{\prime \prime }}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }}.
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| <br>
| |
| | |
| ====Example 4====
| |
| | |
| Using the same data as in the probability plotting example (Example 3), and assuming a 2-parameter Weibull distribution, estimate the parameter using the MLE method.
| |
| <br>
| |
| '''Solution'''
| |
| <br>
| |
| In this case we have non-grouped data with no suspensions, thus Eqns. (mle2w1) and (mle2w2) become:
| |
| | |
| | |
| <br>
| |
| ::<math>\frac{\partial \Lambda }{\partial \beta }=\frac{6}{\beta }+\underset{i=1}{\overset{6}{\mathop{\sum }}}\,\ln \left( \frac{{{T}_{i}}}{\eta } \right)-\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta }}\ln \left( \frac{{{T}_{i}}}{\eta } \right)=0</math>
| |
| | |
| | |
| <br>
| |
| and:
| |
| | |
| | |
| <br>
| |
| ::<math>\frac{\partial \Lambda }{\partial \eta }=\frac{-\beta }{\eta }\cdot 6+\frac{\beta }{\eta }\underset{i=1}{\overset{6}{\mathop \sum }}\,{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta }}=0</math>
| |
| | |
| <br>
| |
| Solving the above equations simultaneously we get:
| |
| | |
| <br>
| |
| ::<math>\begin{matrix}
| |
| \widehat{\beta }=1.933 \\
| |
| \widehat{\eta }=73.526 \\
| |
| \end{matrix}</math>
| |
| | |
| ==The Lognormal Distribution==
| |
| <br>
| |
| | |
| The lognormal distribution is commonly used for general reliability analysis, cycles-to-failure in fatigue, material strengths and loading variables in probabilistic design. A random variable is lognormally distributed if the logarithm of the random variable is normally distributed. Since the logarithms of a lognormally distributed random variable are normally distributed, the lognormal distribution is given by:
| |
| <br>
| |
| | |
| | |
| ::<math>f({T}')=\frac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\bar{{T}'}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}</math>
| |
| | |
| <br>
| |
| | |
| where:
| |
| <br>
| |
| • <math>{T}'=\ln T</math> , and where the <math>T</math> s are the times-to-failure.
| |
| <br>
| |
| • <math>\bar{{T}'}=</math> mean of the natural logarithms of the times to failure.
| |
| <br>
| |
| • <math>{{\sigma }_{{{T}'}}}=</math> standard deviation of the natural logarithms of the times to failure.
| |
| <br>
| |
| The lognormal <math>pdf</math> can be obtained, realizing that for equal probabilities under the normal and lognormal <math>pdf</math> s incremental areas should also be equal, or:
| |
| <br>
| |
| | |
| | |
| ::<math>f(T)dT=f({T}')d{T}'</math>
| |
| <br>
| |
| | |
| Taking the derivative yields:
| |
| | |
| <br>
| |
| ::<math>d{T}'=\frac{dT}{T}</math>
| |
| <br>
| |
| | |
| Substitution yields:
| |
| <br>
| |
| | |
| ::<math>\begin{align}
| |
| & f(T)= & \frac{f({T}')}{T} \\
| |
| & = & \frac{1}{T\cdot {{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\bar{{T}'}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}
| |
| \end{align}</math>
| |
| <br>
| |
| | |
| | |
| where:
| |
| <br>
| |
| | |
| ::<math>f(T)\ge 0,T>0,-\infty <\bar{{T}'}<\infty ,{{\sigma }_{{{T}'}}}>0</math>
| |
| | |
| ===Statistical Properties Summary===
| |
| <br>
| |
| | |
| ====The Mean or MTTF====
| |
| <br>
| |
| | |
| • The mean of the lognormal distribution, <math>\bar{T}</math> , is given by:
| |
| | |
| <br>
| |
| | |
| ::<math>\bar{T}={{e}^{\bar{{T}'}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}}</math>
| |
| | |
| | |
| <br>
| |
| • The mean of the natural logarithms of the times-to-failure, <math>{{\bar{T}}^{^{\prime }}}</math> , in terms of <math>\bar{T}</math> and <math>{{\sigma }_{T}}</math> is given by:
| |
| | |
| <br>
| |
| | |
| ::<math>{{\bar{T}}^{\prime }}=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)</math>
| |
| | |
| | |
| ====The Standard Deviation====
| |
| | |
| • The standard deviation of the lognormal distribution, <math>{{\sigma }_{T}}</math> , is given by:
| |
| | |
| <br>
| |
| | |
| ::<math>{{\sigma }_{T}}=\sqrt{\left( {{e}^{2\bar{{T}'}+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)}</math>
| |
| | |
| <br>
| |
| • The standard deviation of the natural logarithms of the times-to-failure, <math>{{\sigma }_{{{T}'}}}</math> , in terms of <math>\bar{T}</math> and <math>{{\sigma }_{T}}</math> is given by:
| |
| | |
| <br>
| |
| ::<math>{{\sigma }_{{{T}'}}}=\sqrt{\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)}</math>
| |
| | |
| <br>
| |
| ====The Median====
| |
| | |
| <br>
| |
| • The median of the lognormal distribution is given by:
| |
| | |
| | |
| <br>
| |
| ::<math>\breve{T}={{e}^{{{\bar{T}}^{\prime }}}}</math>
| |
| | |
| ====The Mode====
| |
| <br>
| |
| | |
| • The mode of the lognormal distribution is given by:
| |
| | |
| | |
| <br>
| |
| ::<math>\tilde{T}={{e}^{{{\bar{T}}^{\prime }}-\sigma _{{{T}'}}^{2}}}</math>
| |
| | |
| ====Reliability Function====
| |
| | |
| <br>
| |
| For the lognormal distribution, the reliability for a mission of time <math>T</math> , starting at age 0, is given by:
| |
| | |
| | |
| <br>
| |
| ::<math>R(T)=\mathop{}_{T}^{\infty }f(t)dt</math>
| |
| | |
| <br>
| |
| or:
| |
| | |
| | |
| <br>
| |
| ::<math>R(T)=\mathop{}_{{{T}^{^{\prime }}}}^{\infty }\frac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t-\overline{{{T}'}}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt</math>
| |
| | |
| <br>
| |
| There is no closed form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables.
| |
| <br>
| |
| <br>
| |
| ====Lognormal Failure Rate====
| |
| <br>
| |
| The lognormal failure rate is given by:
| |
| | |
| | |
| <br>
| |
| ::<math>\lambda (T)=\frac{f(T)}{R(T)}=\frac{\tfrac{1}{{T}'{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{{T}'-\overline{{{T}'}}}{{{\sigma }_{{{T}'}}}})}^{2}}}}}{\mathop{}_{{{T}'}}^{\infty }\tfrac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{t-\overline{{{T}'}}}{{{\sigma }_{{{T}'}}}})}^{2}}}}dt}</math>
| |
| | |
| | |
| ===Characteristics===
| |
| | |
| <br>
| |
| • The lognormal distribution is a distribution skewed to the right.
| |
| <br>
| |
| • The <math>pdf</math> starts at zero, increases to its mode, and decreases thereafter.
| |
| <br>
| |
| [[File:chp4pdf.gif|center]]
| |
| <br>
| |
| ::Fig. 13: ''Pdf'' of the lognormal distribution.
| |
| <br>
| |
| <br>
| |
| ::<math></math>
| |
| | |
| <br>
| |
| The characteristics of the lognormal distribution can be exemplified by examining the two parameters, the log-mean, <math>({{\overline{T}}^{\prime }}),</math> and the log-std, <math>({{\sigma }_{{{T}'}}}),</math> and the effect they have on the <math>pdf</math> .
| |
| <br>
| |
| Looking at the Log-Mean <math>({{\overline{T}}^{\prime }})</math>
| |
| <br>
| |
| • The parameter, <math>\bar{{T}'}</math> , or the log-mean life, or the <math>MTT{F}'</math> in terms of the logarithm of the <math>{T}'s</math> is also the scale parameter, and is a unitless number.
| |
| <br>
| |
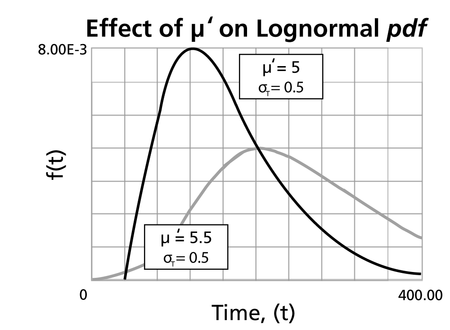
| • For the same <math>{{\sigma }_{{{T}'}}}</math> the <math>pdf</math> 's skewness increases as <math>\bar{{T}'}</math> increases.
| |
| <br>
| |
| <br>
| |
| [[File:chp4pdf2.gif|center]]
| |
| <br>
| |
| ::Fig. 14: ''Pdf'' of the lognormal distribution with different log-mean values.
| |
| <br>
| |
| | |
|
| |
| ====Looking at the Log-STD <math>({{\sigma }_{{{T}'}}})</math>====
| |
| <br>
| |
| • The parameter <math>{{\sigma }_{{{T}'}}}</math> , or the standard deviation of the <math>{T}'s</math> in terms of their logarithm or of their <math>{T}'</math> , is also the shape parameter, and not the scale parameter as in the normal <math>pdf</math> . It is a unitless number and assumes only positive values.
| |
| <br>
| |
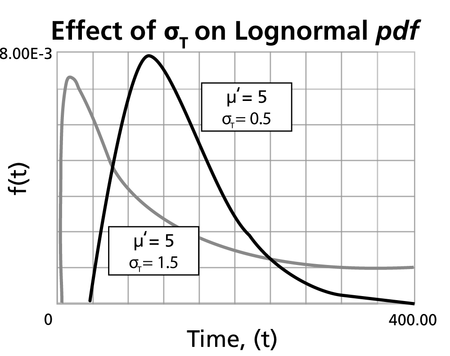
| • The degree of skewness increases as <math>{{\sigma }_{{{T}'}}}</math> increases, for a given <math>\bar{{T}'}</math> .
| |
| <br>
| |
| • For <math>{{\sigma }_{{{T}'}}}</math> values significantly greater than 1, the <math>pdf</math> rises very sharply in the beginning (i.e. for very small values of <math>T</math> near zero), and essentially follows the ordinate axis, peaks out early, and then decreases sharply like an exponential <math>pdf</math> or a Weibull <math>pdf</math> with <math>0<\beta <1</math> .
| |
| <br>
| |
| [[File:chp4pdf3.gif|center]]
| |
| <br>
| |
| ::Fig. 15: ''Pdf'' of the lognormal distribution with different log-std values.
| |
| <br>
| |
| | |
| ===Parameter Estimation===
| |
| | |
| The estimate of the parameters of the lognormal distribution can be found graphically on probability plotting paper or analytically using either least squares or maximum likelihood. (Parameter estimation methods are presented in detail in Appendix B.)
| |
| <br>
| |
| | |
| ====Probability Plotting====
| |
| | |
| <br>
| |
| One method of calculating the parameter of the lognormal distribution is by using probability plotting. To better illustrate this procedure, consider the following example.
| |
| | |
| | |
| <br>
| |
| ====Example 5====
| |
| | |
| | |
| <br>
| |
| Let's assume six identical units are being reliability tested at the same application and operation stress levels. All of these units fail during the test after operating the following times (in hours), <math>{{T}_{i}}</math> : 144, 385, 747, 1,144, 1,576 and 2,616.
| |
| The steps for determining the parameters of the lognormal <math>pdf</math> representing the data, using probability plotting, are as follows:
| |
| <br>
| |
| • Rank the times-to-failure in ascending order as shown next.
| |
|
| |
| <math>\begin{matrix}
| |
| \text{Time-to-} & \text{Failure Order Number} \\
| |
| \text{failure, hrs} & \text{out of a Sample Size of 6} \\
| |
| \text{144} & \text{1} \\
| |
| \text{385} & \text{2} \\
| |
| \text{747} & \text{3} \\
| |
| \text{1,144} & \text{4} \\
| |
| \text{1,576} & \text{5} \\
| |
| \text{2,616} & \text{6} \\
| |
| \end{matrix}</math>
| |
|
| |
|
| |
| • Obtain their median rank plotting positions. The times-to-failure, with their corresponding median ranks, are shown next:
| |
| <br>
| |
| | |
| | |
| ::<math>\begin{matrix}
| |
| \text{Time-to-} & \text{Median} \\
| |
| \text{failure, hr} & \text{Rank, }% \\
| |
| \text{144} & \text{10}\text{.91} \\
| |
| \text{385} & \text{26}\text{.44} \\
| |
| \text{747} & \text{42}\text{.14} \\
| |
| \text{1,144} & \text{57}\text{.86} \\
| |
| \text{1,576} & \text{73}\text{.56} \\
| |
| \text{2,616} & \text{89}\text{.09} \\
| |
| \end{matrix}</math>
| |
| | |
| | |
| • On a lognormal probability paper, plot the times and their corresponding rank value. Fig. 16 displays an example of a lognormal probability paper. The paper is simply a log-log paper. (The solution is given in Fig. 17.)
| |
| | |
| <br>
| |
| [[File:ALTA4.10.gif|center]]
| |
| <br>
| |
| ::Fig. 16: Sample lognormal probability plotting paper.
| |
| <br>
| |
| | |
|
| |
| • Draw the best possible straight line that goes through the <math>t=0</math>
| |
| and <math>R(t)=100%</math> point and through these points (as shown in Fig. 17).
| |
| • At the <math>Q(t)=50%</math> ordinate point, draw a straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of the median. For this case, <math>\breve{T}=760</math> hr which means that <math>{{\bar{T}}^{\prime }}=\ln(\breve{T})=6.633</math>(see Eqn. Median).
| |
| <br>
| |
| | |
| ::<math></math>
| |
| <br>
| |
| [[File:ALTA4.11.gif|center]]
| |
| <br>
| |
| ::Fig. 17: Probability plot for Example 5.
| |
| <br>
| |
| <br>
| |
| • The standard deviation, <math>{{\sigma }_{{{T}'}}},</math> can be found using the following equation:
| |
| | |
| <br>
| |
| | |
| ::<math>\begin{align}
| |
| & {{\sigma }_{{{T}'}}}= & \frac{\ln \left[ T(Q=97.7%) \right]-\ln \left[ T(Q=2.3%) \right]}{4} \\
| |
| & = & \frac{\ln (5100)-\ln (120)}{4} \\
| |
| & = & 0.937376
| |
| \end{align}</math>
| |
| | |
| | |
| <br>
| |
| Now any reliability value for any mission time <math>t</math> can be obtained. For example, the reliability for a mission of 200 hr, or any other time, can now be obtained either from the plot or analytically.
| |
| | |
| <br>
| |
| To obtain the value from the plot, draw a vertical line from the abscissa, at <math>t=200</math> hr, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read <math>Q(t)</math> . In this case, <math>R(t=200)=1-Q(t=200)=92%</math> . This can also be obtained analytically, from the lognormal reliability function. However, standard normal tables (or the Quick Statistical Reference in ALTA) must be used.
| |
| | |
| ====MLE Parameter Estimation====
| |
| | |
| <br>
| |
| The parameters of the lognormal distribution can also be estimated using Maximum Likelihood Estimation (MLE). This general log-likelihood function is:
| |
| | |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{{{\sigma }_{{{T}'}}}{{T}_{i}}}\phi \left( \frac{\ln \left( {{T}_{i}} \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right] \\
| |
| & & \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ 1-\Phi \left( \frac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right]+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })]
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| where:
| |
| | |
| <br>
| |
| ::<math>z_{Li}^{\prime \prime }=\frac{\ln T_{Li}^{\prime \prime }-{\mu }'}{\sigma _{T}^{\prime }}</math>
| |
| | |
| | |
| | |
| <br>
| |
| ::<math>z_{Ri}^{\prime \prime }=\frac{\ln T_{Ri}^{\prime \prime }-{\mu }'}{\sigma _{T}^{\prime }}</math>
| |
| | |
| <br>
| |
| and:
| |
| <br>
| |
| <br>
| |
| • <math>{{F}_{e}}</math> is the number of groups of times-to-failure data points.
| |
| <br>
| |
| • <math>{{N}_{i}}</math> is the number of times-to-failure in the <math>{{i}^{th}}</math> time-to-failure data group.
| |
| <br>
| |
| • <math>{\mu }'</math> is the mean of the natural logarithms of the times-to-failure (unknown a priori, the first of two parameters to be found).
| |
| <br>
| |
| • <math>{{\sigma }_{{{T}'}}}</math> is the standard deviation of the natural logarithms of the times-to-failure (unknown a priori, the second of two parameters to be found).
| |
| <br>
| |
| • <math>{{T}_{i}}</math> is the time of the <math>{{i}^{th}}</math> group of time-to-failure data.
| |
| <br>
| |
| • <math>S</math> is the number of groups of suspension data points.
| |
| <br>
| |
| • <math>N_{i}^{\prime }</math> is the number of suspensions in <math>{{i}^{th}}</math> group of suspension data points.
| |
| <br>
| |
| • <math>T_{i}^{\prime }</math> is the time of the <math>{{i}^{th}}</math> suspension data group.
| |
| <br>
| |
| • <math>FI</math> is the number of interval data groups.
| |
| <br>
| |
| • <math>N_{i}^{\prime \prime }</math> is the number of intervals in the i <math>^{th}</math> group of data intervals.
| |
| <br>
| |
| • <math>T_{Li}^{\prime \prime }</math> is the beginning of the i <math>^{th}</math> interval.
| |
| <br>
| |
| • <math>T_{Ri}^{\prime \prime }</math> is the ending of the i <math>^{th}</math> interval.
| |
| The solution will be found by solving for a pair of parameters <math>\left( {\mu }',{{\sigma }_{{{T}'}}} \right)</math> so that <math>\tfrac{\partial \Lambda }{\partial {\mu }'}=0</math> and <math>\tfrac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}=0,</math> where:
| |
| | |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \frac{\partial \Lambda }{\partial {\mu }'}= & \frac{1}{\sigma _{{{T}'}}^{2}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}(\ln ({{T}_{i}})-{\mu }') \\
| |
| & & +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}\overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\varphi (z_{Ri}^{\prime \prime })-\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))} \\
| |
| & & \\
| |
| & \frac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{\left( \ln ({{T}_{i}})-{\mu }' \right)}^{2}}}{\sigma _{{{T}'}}^{3}}-\frac{1}{{{\sigma }_{{{T}'}}}} \right) \\
| |
| & & +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}\overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{z_{Ri}^{\prime \prime }\varphi (z_{Ri}^{\prime \prime })-z_{Li}^{\prime \prime }\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))}
| |
| \end{align}</math>
| |
| | |
| <br>
| |
| and:
| |
| <br>
| |
| <br>
| |
| ::<math>\phi \left( x \right)=\frac{1}{\sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( x \right)}^{2}}}}</math>
| |
| | |
| | |
| <br>
| |
| ::<math>\Phi (x)=\frac{1}{\sqrt{2\pi }}\mathop{}_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dx</math>
| |
| | |
| | |
| <br>
| |
| ====Example 6====
| |
| | |
| <br>
| |
| Using the same data as in the probability plotting example (Example 5), and assuming a lognormal distribution, estimate the parameters using the MLE method.
| |
| <br>
| |
| <br>
| |
| <br>
| |
| ''Solution''
| |
| <br>
| |
| <br>
| |
| In this example we have non-grouped data without suspensions. Thus, the partials reduce to:
| |
| | |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & \frac{\partial \Lambda }{\partial {\mu }'}= & \frac{1}{\sigma _{{{T}'}}^{2}}\cdot \underset{i=1}{\overset{14}{\mathop \sum }}\,\ln ({{T}_{i}})-{\mu }'=0 \\
| |
| & \frac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}= & \underset{i=1}{\overset{14}{\mathop \sum }}\,\left( \frac{\ln ({{T}_{i}})-{\mu }'}{\sigma _{{{T}'}}^{3}}-\frac{1}{{{\sigma }_{{{T}'}}}} \right)=0
| |
| \end{align}</math>
| |
| | |
| | |
| <br>
| |
| Substituting the values of <math>{{T}_{i}}</math> and solving the above system simultaneously, we get:
| |
| | |
| | |
| <br>
| |
| ::<math>\begin{align}
| |
| & {{\sigma }_{{{T}'}}}= & 0.9537 \\
| |
| & {\mu }'= & 6.6356
| |
| \end{align}</math>
| |
| | |
| | |
| <br>
| |
| The mean and standard deviation of the times-to-failure can be estimated using Eqns. (mean) and (sdv):
| |
| | |
| | |
| <br>
| |
| ::<math>\overline{T}=\mu =1,200.31\text{ }hr</math>
| |
| | |
| | |
| <br>
| |
| and:
| |
| | |
| | |
| <br>
| |
| ::<math>{{\sigma }_{T}}=1,461.78\text{ }hr</math>
| |
| | |
| {{RS Copyright}}
| |
| [[Category:Acclerated_Testing_Reference]
| |
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/accelerated_life_testing_data_analysis
|
Chapter 3: Distributions Used in Accelerated Testing
|
|

| Chapter 3
|
| Distributions Used in Accelerated Testing
|
 Available Software:
ALTA
More Resources:
ALTA Examples
|
In this chapter, we will briefly present three lifetime distributions commonly used in accelerated life test analysis: the exponential, the Weibull and the lognormal distributions. Note that although all forms are mentioned below, ALTA uses the 1-parameter form of the exponential distribution and the 2-parameter form of the Weibull distribution.
Readers who are interested in a more rigorous overview of these distributions (or for information about other life distributions) can refer to the Life data analysis reference. For information about the parameter estimation methods, see Appendix B.
The Exponential Distribution
The exponential distribution is commonly used for components or systems exhibiting a constant failure rate. Due to its simplicity, it has been widely employed, even in cases where it doesn't apply. In its most general case, the 2-parameter exponential distribution is defined by:
- [math]\displaystyle{ \begin{align}
f(t)=\lambda e^{-\lambda (t-\gamma)}
\end{align}\,\! }[/math]
Where [math]\displaystyle{ \lambda\,\! }[/math] is the constant failure rate in failures per unit of measurement (e.g., failures per hour, per cycle, etc.) and [math]\displaystyle{ \gamma\,\! }[/math] is the location parameter. In addition, [math]\displaystyle{ \lambda =\tfrac{1}{m}\,\! }[/math], where [math]\displaystyle{ {m}\,\! }[/math] is the mean time between failures (or to failure).
If the location parameter, [math]\displaystyle{ \gamma\,\! }[/math], is assumed to be zero, then the distribution becomes the 1-parameter exponential or:
- [math]\displaystyle{ \begin{align}
f(t)=\lambda e^{-\lambda t}
\end{align}\,\! }[/math]
For a detailed discussion of this distribution, see The Exponential Distribution.
Exponential Distribution Functions
The Mean or MTTF
The mean, [math]\displaystyle{ \overline{T},\,\! }[/math] or mean time to failure (MTTF) is given by:
- [math]\displaystyle{ \begin{align}
\bar{T}= & \int_{\gamma }^{\infty }t\cdot f(t)dt \\
= & \int_{\gamma }^{\infty }t\cdot \lambda \cdot {{e}^{-\lambda t}}dt \\
= & \gamma +\frac{1}{\lambda }=m
\end{align}\,\! }[/math]
Note that when [math]\displaystyle{ \gamma =0\,\! }[/math], the MTTF is the inverse of the exponential distribution's constant failure rate. This is only true for the exponential distribution. Most other distributions do not have a constant failure rate. Consequently, the inverse relationship between failure rate and MTTF does not hold for these other distributions.
The Median
The median, [math]\displaystyle{ \breve{T}, \,\! }[/math] is:
- [math]\displaystyle{ \breve{T}=\gamma +\frac{1}{\lambda}\cdot 0.693 \,\! }[/math]
The Mode
The mode, [math]\displaystyle{ \tilde{T},\,\! }[/math] is:
- [math]\displaystyle{ \tilde{T}=\gamma \,\! }[/math]
The Standard Deviation
The standard deviation, [math]\displaystyle{ {\sigma }_{T}\,\! }[/math], is:
- [math]\displaystyle{ {\sigma}_{T}=\frac{1}{\lambda }=m\,\! }[/math]
The Exponential Reliability Function
The equation for the 2-parameter exponential cumulative density function, or cdf, is given by:
- [math]\displaystyle{ \begin{align}
F(t)=Q(t)=1-{{e}^{-\lambda (t-\gamma )}}
\end{align}\,\! }[/math]
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function of the 2-parameter exponential distribution is given by:
- [math]\displaystyle{ R(t)=1-Q(t)=1-\int_{0}^{t-\gamma }f(x)dx\,\! }[/math]
- [math]\displaystyle{ R(t)=1-\int_{0}^{t-\gamma }\lambda {{e}^{-\lambda x}}dx={{e}^{-\lambda (t-\gamma )}}\,\! }[/math]
The 1-parameter exponential reliability function is given by:
- [math]\displaystyle{ R(t)={{e}^{-\lambda t}}={{e}^{-\tfrac{t}{m}}}\,\! }[/math]
The Exponential Conditional Reliability Function
The exponential conditional reliability equation gives the reliability for a mission of [math]\displaystyle{ t\,\! }[/math] duration, having already successfully accumulated [math]\displaystyle{ T\,\! }[/math] hours of operation up to the start of this new mission. The exponential conditional reliability function is:
- [math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)}=\frac{{{e}^{-\lambda (T+t-\gamma )}}}{{{e}^{-\lambda (T-\gamma )}}}={{e}^{-\lambda t}}\,\! }[/math]
which says that the reliability for a mission of [math]\displaystyle{ t\,\! }[/math] duration undertaken after the component or equipment has already accumulated [math]\displaystyle{ T\,\! }[/math] hours of operation from age zero is only a function of the mission duration, and not a function of the age at the beginning of the mission. This is referred to as the memoryless property.
The Exponential Reliable Life Function
The reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}\,\! }[/math], for the 1-parameter exponential distribution is:
- [math]\displaystyle{ R({{t}_{R}})={{e}^{-\lambda ({{t}_{R}}-\gamma )}}\,\! }[/math]
- [math]\displaystyle{ \begin{align}
\ln[R({{t}_{R}})]=-\lambda({{t}_{R}}-\gamma )
\end{align}\,\! }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=\gamma -\frac{\ln [R({{t}_{R}})]}{\lambda }\,\! }[/math]
The Exponential Failure Rate Function
The exponential failure rate function is:
- [math]\displaystyle{ \lambda (t)=\frac{f(t)}{R(t)}=\frac{\lambda {{e}^{-\lambda (t-\gamma )}}}{{{e}^{-\lambda (t-\gamma )}}}=\lambda =\text{constant}\,\! }[/math]
Once again, note that the constant failure rate is a characteristic of the exponential distribution, and special cases of other distributions only. Most other distributions have failure rates that are functions of time.
Characteristics of the Exponential Distribution
The primary trait of the exponential distribution is that it is used for modeling the behavior of items with a constant failure rate. It has a fairly simple mathematical form, which makes it fairly easy to manipulate. Unfortunately, this fact also leads to the use of this model in situations where it is not appropriate. For example, it would not be appropriate to use the exponential distribution to model the reliability of an automobile. The constant failure rate of the exponential distribution would require the assumption that the automobile would be just as likely to experience a breakdown during the first mile as it would during the one-hundred-thousandth mile. Clearly, this is not a valid assumption. However, some inexperienced practitioners of reliability engineering and life data analysis will overlook this fact, lured by the siren-call of the exponential distribution's relatively simple mathematical models.
The Effect of lambda and gamma on the Exponential pdf
- The exponential pdf has no shape parameter, as it has only one shape.
- The exponential pdf is always convex and is stretched to the right as [math]\displaystyle{ \lambda \,\! }[/math] decreases in value.
- The value of the pdf function is always equal to the value of [math]\displaystyle{ \lambda \,\! }[/math] at [math]\displaystyle{ t=0\,\! }[/math] (or [math]\displaystyle{ t=\gamma \,\! }[/math]).
- The location parameter, [math]\displaystyle{ \gamma \,\! }[/math], if positive, shifts the beginning of the distribution by a distance of [math]\displaystyle{ \gamma \,\! }[/math] to the right of the origin, signifying that the chance failures start to occur only after [math]\displaystyle{ \gamma \,\! }[/math] hours of operation, and cannot occur before this time.
- The scale parameter is [math]\displaystyle{ \tfrac{1}{\lambda }=\bar{T}-\gamma =m-\gamma \,\! }[/math].
- As [math]\displaystyle{ t\to \infty \,\! }[/math], [math]\displaystyle{ f(t)\to 0\,\! }[/math].
The Effect of lambda and gamma on the Exponential Reliability Function
- The 1-parameter exponential reliability function starts at the value of 100% at [math]\displaystyle{ t=0\,\! }[/math], decreases thereafter monotonically and is convex.
- The 2-parameter exponential reliability function remains at the value of 100% for [math]\displaystyle{ t=0\,\! }[/math] up to [math]\displaystyle{ t=\gamma \,\! }[/math], and decreases thereafter monotonically and is convex.
- As [math]\displaystyle{ t\to \infty \,\! }[/math], [math]\displaystyle{ R(t\to \infty )\to 0\,\! }[/math].
- The reliability for a mission duration of [math]\displaystyle{ t=m=\tfrac{1}{\lambda }\,\! }[/math], or of one MTTF duration, is always equal to [math]\displaystyle{ 0.3679\,\! }[/math] or 36.79%. This means that the reliability for a mission which is as long as one MTTF is relatively low and is not recommended because only 36.8% of the missions will be completed successfully. In other words, of the equipment undertaking such a mission, only 36.8% will survive their mission.
The Effect of lambda and gamma on the Failure Rate Function
- The 1-parameter exponential failure rate function is constant and starts at [math]\displaystyle{ t=0\,\! }[/math].
- The 2-parameter exponential failure rate function remains at the value of 0 for [math]\displaystyle{ t=0\,\! }[/math] up to [math]\displaystyle{ t=\gamma \,\! }[/math], and then keeps at the constant value of [math]\displaystyle{ \lambda\,\! }[/math].
The Weibull Distribution
The Weibull distribution is a general purpose reliability distribution used to model material strength, times-to-failure of electronic and mechanical components, equipment or systems. In its most general case, the 3-parameter Weibull pdf is defined by:
- [math]\displaystyle{ f(t)=\frac{\beta}{\eta } \left( \frac{t-\gamma }{\eta } \right)^{\beta -1}{e}^{-(\tfrac{t-\gamma }{\eta }) ^{\beta}}\,\! }[/math]
where [math]\displaystyle{ \beta \,\! }[/math] = shape parameter, [math]\displaystyle{ \eta \,\! }[/math] = scale parameter and [math]\displaystyle{ \gamma\,\! }[/math] = location parameter.
If the location parameter, [math]\displaystyle{ \gamma\,\! }[/math], is assumed to be zero, then the distribution becomes the 2-parameter Weibull or:
- [math]\displaystyle{ f(t)=\frac{\beta}{\eta }( \frac{t }{\eta } )^{\beta -1}{e}^{-(\tfrac{t }{\eta }) ^{\beta}}\,\! }[/math]
One additional form is the 1-parameter Weibull distribution, which assumes that the location parameter, [math]\displaystyle{ \gamma\,\! }[/math] is zero, and the shape parameter is a known constant, or [math]\displaystyle{ \beta \,\! }[/math] = constant = [math]\displaystyle{ C\,\! }[/math], so:
- [math]\displaystyle{ f(t)=\frac{C}{\eta}(\frac{t}{\eta})^{C-1}e^{-(\frac{t}{\eta})^C}
\,\! }[/math]
For a detailed discussion of this distribution, see The Weibull Distribution.
Weibull Distribution Functions
The Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} \,\! }[/math], (also called MTTF) of the Weibull pdf is given by:
- [math]\displaystyle{ \overline{T}=\gamma +\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
where
- [math]\displaystyle{ \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
is the gamma function evaluated at the value of:
- [math]\displaystyle{ \left( { \frac{1}{\beta }}+1\right) \,\! }[/math]
The gamma function is defined as:
- [math]\displaystyle{ \Gamma (n)=\int_{0}^{\infty }e^{-x}x^{n-1}dx \,\! }[/math]
For the 2-parameter case, this can be reduced to:
- [math]\displaystyle{ \overline{T}=\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
Note that some practitioners erroneously assume that [math]\displaystyle{ \eta \,\! }[/math] is equal to the MTTF, [math]\displaystyle{ \overline{T}\,\! }[/math].
This is only true for the case of:
[math]\displaystyle{ \beta=1 \,\! }[/math] or:
- [math]\displaystyle{
\begin{align}
\overline{T} &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\
&= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\
&= \eta \cdot \Gamma \left( {2}\right) \\
&= \eta \cdot 1\\
&= \eta
\end{align}
\,\! }[/math]
The Median
The median, [math]\displaystyle{ \breve{T}\,\! }[/math], of the Weibull distribution is given by:
- [math]\displaystyle{ \breve{T}=\gamma +\eta \left( \ln 2\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Mode
The mode, [math]\displaystyle{ \tilde{T} \,\! }[/math], is given by:
- [math]\displaystyle{ \tilde{T}=\gamma +\eta \left( 1-\frac{1}{\beta }\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Standard Deviation
The standard deviation, [math]\displaystyle{ \sigma _{T}\,\! }[/math], is given by:
- [math]\displaystyle{ \sigma _{T}=\eta \cdot \sqrt{\Gamma \left( {\frac{2}{\beta }}+1\right) -\Gamma \left( {\frac{1}{ \beta }}+1\right) ^{2}} \,\! }[/math]
The Weibull Reliability Function
The equation for the 3-parameter Weibull cumulative density function, cdf, is given by:
- [math]\displaystyle{ F(t)=1-e^{-\left( \frac{t-\gamma }{\eta }\right) ^{\beta }} \,\! }[/math]
This is also referred to as unreliability and designated as [math]\displaystyle{ Q(t) \,\! }[/math] by some authors.
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function for the 3-parameter Weibull distribution is then given by:
- [math]\displaystyle{ R(t)=e^{-\left( { \frac{t-\gamma }{\eta }}\right) ^{\beta }} \,\! }[/math]
The Weibull Conditional Reliability Function
The 3-parameter Weibull conditional reliability function is given by:
- [math]\displaystyle{ R(t|T)={ \frac{R(T+t)}{R(T)}}={\frac{e^{-\left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }}}{e^{-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }}}} \,\! }[/math]
or:
- [math]\displaystyle{ R(t|T)=e^{-\left[ \left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }\right] } \,\! }[/math]
These give the reliability for a new mission of [math]\displaystyle{ t \,\! }[/math] duration, having already accumulated [math]\displaystyle{ T \,\! }[/math] time of operation up to the start of this new mission, and the units are checked out to assure that they will start the next mission successfully. It is called conditional because you can calculate the reliability of a new mission based on the fact that the unit or units already accumulated hours of operation successfully.
The Weibull Reliable Life
The reliable life, [math]\displaystyle{ T_{R}\,\! }[/math], of a unit for a specified reliability, [math]\displaystyle{ R\,\! }[/math], starting the mission at age zero, is given by:
- [math]\displaystyle{ T_{R}=\gamma +\eta \cdot \left\{ -\ln ( R ) \right\} ^{ \frac{1}{\beta }} \,\! }[/math]
This is the life for which the unit/item will be functioning successfully with a reliability of [math]\displaystyle{ R\,\! }[/math]. If [math]\displaystyle{ R = 0.50\,\! }[/math], then [math]\displaystyle{ T_{R}=\breve{T} \,\! }[/math], the median life, or the life by which half of the units will survive.
The Weibull Failure Rate Function
The Weibull failure rate function, [math]\displaystyle{ \lambda(t) \,\! }[/math], is given by:
- [math]\displaystyle{ \lambda \left( t\right) = \frac{f\left( t\right) }{R\left( t\right) }=\frac{\beta }{\eta }\left( \frac{ t-\gamma }{\eta }\right) ^{\beta -1} \,\! }[/math]
Characteristics of the Weibull Distribution
The Weibull distribution is widely used in reliability and life data analysis due to its versatility. Depending on the values of the parameters, the Weibull distribution can be used to model a variety of life behaviors. We will now examine how the values of the shape parameter, [math]\displaystyle{ \beta\,\! }[/math], and the scale parameter, [math]\displaystyle{ \eta\,\! }[/math], affect such distribution characteristics as the shape of the curve, the reliability and the failure rate. Note that in the rest of this section we will assume the most general form of the Weibull distribution, (i.e., the 3-parameter form). The appropriate substitutions to obtain the other forms, such as the 2-parameter form where [math]\displaystyle{ \gamma = 0,\,\! }[/math] or the 1-parameter form where [math]\displaystyle{ \beta = C = \,\! }[/math] constant, can easily be made.
Effects of the Shape Parameter, beta
The Weibull shape parameter, [math]\displaystyle{ \beta\,\! }[/math], is also known as the slope. This is because the value of [math]\displaystyle{ \beta\,\! }[/math] is equal to the slope of the regressed line in a probability plot. Different values of the shape parameter can have marked effects on the behavior of the distribution. In fact, some values of the shape parameter will cause the distribution equations to reduce to those of other distributions. For example, when [math]\displaystyle{ \beta = 1\,\! }[/math], the pdf of the 3-parameter Weibull distribution reduces to that of the 2-parameter exponential distribution or:
- [math]\displaystyle{ f(t)={\frac{1}{\eta }}e^{-{\frac{t-\gamma }{\eta }}} \,\! }[/math]
where [math]\displaystyle{ \frac{1}{\eta }=\lambda = \,\! }[/math] failure rate. The parameter [math]\displaystyle{ \beta\,\! }[/math] is a pure number, (i.e., it is dimensionless).
The following figure shows the effect of different values of the shape parameter, [math]\displaystyle{ \beta\,\! }[/math], on the shape of the pdf. As you can see, the shape can take on a variety of forms based on the value of [math]\displaystyle{ \beta\,\! }[/math].
For [math]\displaystyle{ 0\lt \beta \leq 1 \,\! }[/math]:
- As [math]\displaystyle{ t \rightarrow 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\! }[/math]), [math]\displaystyle{ f(t)\rightarrow \infty.\,\! }[/math]
- As [math]\displaystyle{ t\rightarrow \infty\,\! }[/math], [math]\displaystyle{ f(t)\rightarrow 0\,\! }[/math].
- [math]\displaystyle{ f(t)\,\! }[/math] decreases monotonically and is convex as it increases beyond the value of [math]\displaystyle{ \gamma\,\! }[/math].
- The mode is non-existent.
For [math]\displaystyle{ \beta \gt 1 \,\! }[/math]:
- [math]\displaystyle{ f(t) = 0\,\! }[/math] at [math]\displaystyle{ t = 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\! }[/math]).
- [math]\displaystyle{ f(t)\,\! }[/math] increases as [math]\displaystyle{ t\rightarrow \tilde{T} \,\! }[/math] (the mode) and decreases thereafter.
- For [math]\displaystyle{ \beta \lt 2.6\,\! }[/math] the Weibull pdf is positively skewed (has a right tail), for [math]\displaystyle{ 2.6 \lt \beta \lt 3.7\,\! }[/math] its coefficient of skewness approaches zero (no tail). Consequently, it may approximate the normal pdf, and for [math]\displaystyle{ \beta \gt 3.7\,\! }[/math] it is negatively skewed (left tail). The way the value of [math]\displaystyle{ \beta\,\! }[/math] relates to the physical behavior of the items being modeled becomes more apparent when we observe how its different values affect the reliability and failure rate functions. Note that for [math]\displaystyle{ \beta = 0.999\,\! }[/math], [math]\displaystyle{ f(0) = \infty\,\! }[/math], but for [math]\displaystyle{ \beta = 1.001\,\! }[/math], [math]\displaystyle{ f(0) = 0.\,\! }[/math] This abrupt shift is what complicates MLE estimation when [math]\displaystyle{ \beta\,\! }[/math] is close to 1.
The Effect of beta on the cdf and Reliability Function
The above figure shows the effect of the value of [math]\displaystyle{ \beta\,\! }[/math] on the cdf, as manifested in the Weibull probability plot. It is easy to see why this parameter is sometimes referred to as the slope. Note that the models represented by the three lines all have the same value of [math]\displaystyle{ \eta\,\! }[/math]. The following figure shows the effects of these varied values of [math]\displaystyle{ \beta\,\! }[/math] on the reliability plot, which is a linear analog of the probability plot.
- [math]\displaystyle{ R(t)\,\! }[/math] decreases sharply and monotonically for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] and is convex.
- For [math]\displaystyle{ \beta = 1\,\! }[/math], [math]\displaystyle{ R(t)\,\! }[/math] decreases monotonically but less sharply than for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] and is convex.
- For [math]\displaystyle{ \beta \gt 1\,\! }[/math], [math]\displaystyle{ R(t)\,\! }[/math] decreases as increases. As wear-out sets in, the curve goes through an inflection point and decreases sharply.
The Effect of beta on the Weibull Failure Rate
The value of [math]\displaystyle{ \beta\,\! }[/math] has a marked effect on the failure rate of the Weibull distribution and inferences can be drawn about a population's failure characteristics just by considering whether the value of [math]\displaystyle{ \beta\,\! }[/math] is less than, equal to, or greater than one.
As indicated by above figure, populations with [math]\displaystyle{ \beta \lt 1\,\! }[/math] exhibit a failure rate that decreases with time, populations with [math]\displaystyle{ \beta = 1\,\! }[/math] have a constant failure rate (consistent with the exponential distribution) and populations with [math]\displaystyle{ \beta \gt 1\,\! }[/math] have a failure rate that increases with time. All three life stages of the bathtub curve can be modeled with the Weibull distribution and varying values of [math]\displaystyle{ \beta\,\! }[/math]. The Weibull failure rate for [math]\displaystyle{ 0 \lt \beta \lt 1\,\! }[/math] is unbounded at [math]\displaystyle{ T = 0\,\! }[/math] (or [math]\displaystyle{ \gamma\,\!)\,\! }[/math]. The failure rate, [math]\displaystyle{ \lambda(t),\,\! }[/math] decreases thereafter monotonically and is convex, approaching the value of zero as [math]\displaystyle{ t\rightarrow \infty\,\! }[/math] or [math]\displaystyle{ \lambda (\infty) = 0\,\! }[/math]. This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When encountering such behavior in a manufactured product, it may be indicative of problems in the production process, inadequate burn-in, substandard parts and components, or problems with packaging and shipping. For [math]\displaystyle{ \beta = 1\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] yields a constant value of [math]\displaystyle{ { \frac{1}{\eta }} \,\! }[/math] or:
- [math]\displaystyle{ \lambda (t)=\lambda ={\frac{1}{\eta }} \,\! }[/math]
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
For [math]\displaystyle{ \beta \gt 1\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] increases as [math]\displaystyle{ t\,\! }[/math] increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For [math]\displaystyle{ 1 \lt \beta \lt 2,\,\! }[/math] the [math]\displaystyle{ \lambda(t)\,\! }[/math] curve is concave, consequently the failure rate increases at a decreasing rate as [math]\displaystyle{ t\,\! }[/math] increases.
For [math]\displaystyle{ \beta = 2\,\! }[/math] there emerges a straight line relationship between [math]\displaystyle{ \lambda(t)\,\! }[/math] and [math]\displaystyle{ t\,\! }[/math], starting at a value of [math]\displaystyle{ \lambda(t) = 0\,\! }[/math] at [math]\displaystyle{ t = \gamma\,\! }[/math], and increasing thereafter with a slope of [math]\displaystyle{ { \frac{2}{\eta ^{2}}} \,\! }[/math]. Consequently, the failure rate increases at a constant rate as [math]\displaystyle{ t\,\! }[/math] increases. Furthermore, if [math]\displaystyle{ \eta = 1\,\! }[/math] the slope becomes equal to 2, and when [math]\displaystyle{ \gamma = 0\,\! }[/math], [math]\displaystyle{ \lambda(t)\,\! }[/math] becomes a straight line which passes through the origin with a slope of 2. Note that at [math]\displaystyle{ \beta = 2\,\! }[/math], the Weibull distribution equations reduce to that of the Rayleigh distribution.
When [math]\displaystyle{ \beta \gt 2,\,\! }[/math] the [math]\displaystyle{ \lambda(t)\,\! }[/math] curve is convex, with its slope increasing as [math]\displaystyle{ t\,\! }[/math] increases. Consequently, the failure rate increases at an increasing rate as [math]\displaystyle{ t\,\! }[/math] increases, indicating wearout life.
Effects of the Scale Parameter, eta
A change in the scale parameter [math]\displaystyle{ \eta\,\! }[/math] has the same effect on the distribution as a change of the abscissa scale. Increasing the value of [math]\displaystyle{ \eta\,\! }[/math] while holding [math]\displaystyle{ \beta\,\! }[/math] constant has the effect of stretching out the pdf. Since the area under a pdf curve is a constant value of one, the "peak" of the pdf curve will also decrease with the increase of [math]\displaystyle{ \eta\,\! }[/math], as indicated in the above figure.
- If [math]\displaystyle{ \eta\,\! }[/math] is increased while [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math] are kept the same, the distribution gets stretched out to the right and its height decreases, while maintaining its shape and location.
- If [math]\displaystyle{ \eta\,\! }[/math] is decreased while [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \gamma\,\! }[/math] are kept the same, the distribution gets pushed in towards the left (i.e., towards its beginning or towards 0 or [math]\displaystyle{ \gamma\,\! }[/math]), and its height increases.
- [math]\displaystyle{ \eta\,\! }[/math] has the same units as [math]\displaystyle{ t\,\! }[/math], such as hours, miles, cycles, actuations, etc.
Effects of the Location Parameter, gamma
The location parameter, [math]\displaystyle{ \gamma\,\! }[/math], as the name implies, locates the distribution along the abscissa. Changing the value of [math]\displaystyle{ \gamma\,\! }[/math] has the effect of sliding the distribution and its associated function either to the right (if [math]\displaystyle{ \gamma \gt 0\,\! }[/math]) or to the left (if [math]\displaystyle{ \gamma \lt 0\,\! }[/math]).
- When [math]\displaystyle{ \gamma = 0,\,\! }[/math] the distribution starts at [math]\displaystyle{ t=0\,\! }[/math] or at the origin.
- If [math]\displaystyle{ \gamma \gt 0,\,\! }[/math] the distribution starts at the location [math]\displaystyle{ \gamma\,\! }[/math] to the right of the origin.
- If [math]\displaystyle{ \gamma \lt 0,\,\! }[/math] the distribution starts at the location [math]\displaystyle{ \gamma\,\! }[/math] to the left of the origin.
- [math]\displaystyle{ \gamma\,\! }[/math] provides an estimate of the earliest time-to-failure of such units.
- The life period 0 to [math]\displaystyle{ + \gamma\,\! }[/math] is a failure free operating period of such units.
- The parameter [math]\displaystyle{ \gamma\,\! }[/math] may assume all values and provides an estimate of the earliest time a failure may be observed. A negative [math]\displaystyle{ \gamma\,\! }[/math] may indicate that failures have occurred prior to the beginning of the test, namely during production, in storage, in transit, during checkout prior to the start of a mission, or prior to actual use.
- [math]\displaystyle{ \gamma\,\! }[/math] has the same units as [math]\displaystyle{ t\,\! }[/math], such as hours, miles, cycles, actuations, etc.
The Lognormal Distribution
The lognormal distribution is commonly used for general reliability analysis, cycles-to-failure in fatigue, material strengths and loading variables in probabilistic design. When the natural logarithms of the times-to-failure are normally distributed, then we say that the data follow the lognormal distribution.
The pdf of the lognormal distribution is given by:
- [math]\displaystyle{ \begin{align}
& f(t)=\frac{1}{t{\sigma}'\sqrt{2\pi}}e^{-\tfrac{1}{2}(\tfrac{t'-{\mu'}}{\sigma'})^2}\\
& f(t)\ge 0,t\gt 0,{\sigma'}\gt 0 \\
& {t'}= \ln (t)
\end{align}\,\!
}[/math]
where [math]\displaystyle{ {\mu'}\,\! }[/math] is the mean of the natural logarithms of the times-to-failure and [math]\displaystyle{ {\sigma'}\,\! }[/math] is the standard deviation of the natural logarithms of the times to failure.
For a detailed discussion of this distribution, see The Lognormal Distribution.
Lognormal Distribution Functions
The Mean or MTTF
The mean of the lognormal distribution, [math]\displaystyle{ \mu \,\! }[/math], is discussed in Kececioglu [19]:
- [math]\displaystyle{ \mu ={{e}^{{\mu }'+\tfrac{1}{2}\sigma'^{2}}}\,\! }[/math]
The mean of the natural logarithms of the times-to-failure, [math]\displaystyle{ \mu'\,\! }[/math], in terms of [math]\displaystyle{ \bar{T}\,\! }[/math] and [math]\displaystyle{ {{\sigma}}\,\! }[/math] is given by:
- [math]\displaystyle{ {\mu }'=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma^{2}}{{{{\bar{T}}}^{2}}}+1 \right)\,\! }[/math]
The Median
The median of the lognormal distribution, [math]\displaystyle{ \breve{T}\,\! }[/math], is discussed in Kececioglu [19]:
- [math]\displaystyle{ \breve{T}={{e}^{{{\mu}'}}}\,\! }[/math]
The Mode
The mode of the lognormal distribution, [math]\displaystyle{ \tilde{T}\,\! }[/math], is discussed in Kececioglu [19]:
- [math]\displaystyle{ \tilde{T}={{e}^{{\mu }'-\sigma'^{2}}}\,\! }[/math]
The Standard Deviation
The standard deviation of the lognormal distribution, [math]\displaystyle{ {\sigma }_{T}\,\! }[/math], is discussed in Kececioglu [19]:
- [math]\displaystyle{ {\sigma}_{T} =\sqrt{\left( {{e}^{2\mu '+\sigma {{'}^{2}}}} \right)\left( {{e}^{\sigma {{'}^{2}}}}-1 \right)}\,\! }[/math]
The standard deviation of the natural logarithms of the times-to-failure, [math]\displaystyle{ {\sigma}'\,\! }[/math], in terms of [math]\displaystyle{ \bar{T}\,\! }[/math] and [math]\displaystyle{ {\sigma}\,\! }[/math] is given by:
- [math]\displaystyle{ \sigma '=\sqrt{\ln \left( \frac{{\sigma}_{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)}\,\! }[/math]
The Lognormal Reliability Function
The reliability for a mission of time [math]\displaystyle{ t\,\! }[/math], starting at age 0, for the lognormal distribution is determined by:
- [math]\displaystyle{ R(t)=\int_{t}^{\infty }f(x)dx\,\! }[/math]
or:
- [math]\displaystyle{ {{R}({t})}=\int_{\text{ln}(t)}^{\infty }\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx\,\! }[/math]
As with the normal distribution, there is no closed-form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability we will not discuss manual solution methods. For interested readers, full explanations can be found in the references.
The Lognormal Conditional Reliability Function
The lognormal conditional reliability function is given by:
- [math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)}=\frac{\int_{\text{ln}(T+t)}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}ds}{\int_{\text{ln}(T)}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx}\,\! }[/math]
Once again, the use of standard normal tables is necessary to solve this equation, as no closed-form solution exists.
The Lognormal Reliable Life Function
As there is no closed-form solution for the lognormal reliability equation, no closed-form solution exists for the lognormal reliable life either. In order to determine this value, one must solve the following equation for [math]\displaystyle{ t\,\! }[/math]:
- [math]\displaystyle{ {{R}_{t}}=\int_{\text{ln}(t)}^{\infty }\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx\,\! }[/math]
The Lognormal Failure Rate Function
The lognormal failure rate is given by:
- [math]\displaystyle{ \lambda (t)=\frac{f(t)}{R(t)}=\frac{\tfrac{1}{t\cdot {{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{{t}'-{\mu }'}{{{\sigma' }}})}^{2}}}}}{\int_{{{t}'}}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{x-{\mu }'}{{{\sigma' }}})}^{2}}}}dx}\,\! }[/math]
As with the reliability equations, standard normal tables will be required to solve for this function.
Characteristics of the Lognormal Distribution
- The lognormal distribution is a distribution skewed to the right.
- The pdf starts at zero, increases to its mode, and decreases thereafter.
- The degree of skewness increases as [math]\displaystyle{ {{\sigma'}}\,\! }[/math] increases, for a given [math]\displaystyle{ \mu'\,\! }[/math]
- For the same [math]\displaystyle{ {{\sigma'}}\,\! }[/math], the pdf 's skewness increases as [math]\displaystyle{ {\mu }'\,\! }[/math] increases.
- For [math]\displaystyle{ {{\sigma' }}\,\! }[/math] values significantly greater than 1, the pdf rises very sharply in the beginning, (i.e., for very small values of [math]\displaystyle{ T\,\! }[/math] near zero), and essentially follows the ordinate axis, peaks out early, and then decreases sharply like an exponential pdf or a Weibull pdf with [math]\displaystyle{ 0\lt \beta \lt 1\,\! }[/math].
- The parameter, [math]\displaystyle{ {\mu }'\,\! }[/math], in terms of the logarithm of the [math]\displaystyle{ {T}'s\,\! }[/math] is also the scale parameter, and not the location parameter as in the case of the normal pdf.
- The parameter [math]\displaystyle{ {{\sigma'}}\,\! }[/math], or the standard deviation of the [math]\displaystyle{ {T}'s\,\! }[/math] in terms of their logarithm or of their [math]\displaystyle{ {T}'\,\! }[/math], is also the shape parameter and not the scale parameter, as in the normal pdf, and assumes only positive values.
Lognormal Distribution Parameters in ReliaSoft's Software
In ReliaSoft's software, the parameters returned for the lognormal distribution are always logarithmic. That is: the parameter [math]\displaystyle{ {\mu }'\,\! }[/math] represents the mean of the natural logarithms of the times-to-failure, while [math]\displaystyle{ {{\sigma' }}\,\! }[/math] represents the standard deviation of these data point logarithms. Specifically, the returned [math]\displaystyle{ {{\sigma' }}\,\! }[/math] is the square root of the variance of the natural logarithms of the data points. Even though the application denotes these values as mean and standard deviation, the user is reminded that these are given as the parameters of the distribution, and are thus the mean and standard deviation of the natural logarithms of the data. The mean value of the times-to-failure, not used as a parameter, as well as the standard deviation can be obtained through the QCP or the Function Wizard.

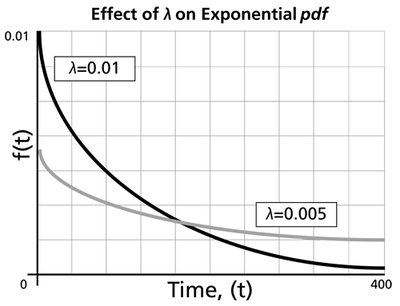
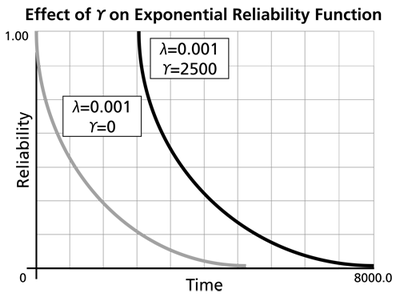
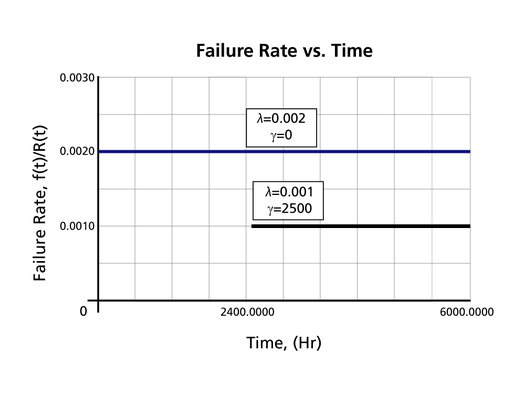
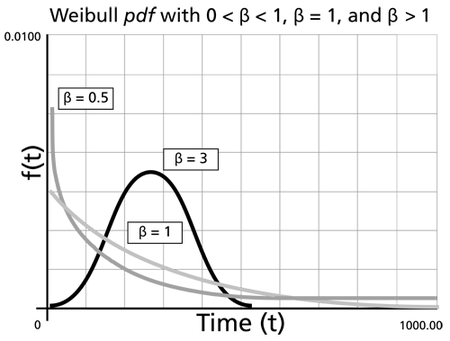
![Effect on [math]\displaystyle{ \beta\,\! }[/math] on the cdf on the Weibull probability plot with a fixed value of [math]\displaystyle{ \eta\,\! }[/math]](/images/b/bf/WB.8_effect_of_weibull.png)
![The effect of values of [math]\displaystyle{ \beta\,\! }[/math] on the Weibull reliability plot.](/images/0/0c/WB.8_weibull_reliability.png)
![The effect of [math]\displaystyle{ \beta\,\! }[/math] on the Weibull failure rate function.](/images/9/9c/WB.8_weibull_failure.png)
![The effects of [math]\displaystyle{ \eta\,\! }[/math] on the Weibull pdf for a common [math]\displaystyle{ \beta\,\! }[/math].](/images/thumb/d/da/WB.8_effects_of_n.png/450px-WB.8_effects_of_n.png)
![The effect of a positive location parameter, [math]\displaystyle{ \gamma\,\! }[/math], on the position of the Weibull pdf.](/images/thumb/8/8b/WB.8_location_parameter.png/450px-WB.8_location_parameter.png)