1P-Exponential MLE Solution for Interval Data: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(3 intermediate revisions by the same user not shown)
Line 1: Line 1:
{{InProgress}}
{{Reference Example}}
{{Reference Example}}


Compares the MLE solution, likelihood ratio bound and Fisher Matrix bound for a 1-parameter exponential distribution with interval data.
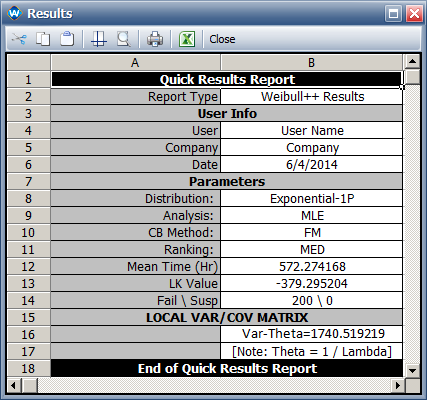
This example validates the calculations for the MLE solution, likelihood ratio bound and Fisher Matrix bound for a 1-parameter exponential distribution with interval data in Weibull++ standard folios.
 


{{Reference_Example_Heading1}}
{{Reference_Example_Heading1}}
Line 33: Line 33:


{{Reference_Example_Heading3}}
{{Reference_Example_Heading3}}
The cumulative distribution function for an exponential distribution is:  
The cumulative distribution function for an exponential distribution is:  


Line 38: Line 39:




The ML estimate <math>\hat{\theta}\,\!</math> = 572.3, and the standard deviation is <math>se_{\hat\theta}\,\!</math> = 41.72. Therefore the variance is 1740.56. The 95% 2-sided confidence interval for <math>{\theta}\,\!</math> are:
The ML estimate <math>\hat{\theta}\,\!</math> = 572.3, and the standard deviation is <math>se_{\hat\theta}\,\!</math> = 41.72. Therefore the variance is 1740.56.  
 


The 95% 2-sided confidence interval for <math>{\theta}\,\!</math> are:


* Based on the likelihood ratio, the confidence interval is [498, 662]. The calculation is based on
* Based on the likelihood ratio, the confidence interval is [498, 662]. The calculation is based on


::<math>-2ln\left [ \frac{L(\theta)}{L(\hat{\theta})} \right ] = X^{2}_{(0.90,1)}\,\!</math>
::<math>-2ln\left [ \frac{L(\theta)}{L(\hat{\theta})} \right ] = X^{2}_{(0.90,1)}\,\!</math>
Line 53: Line 55:


::<math>\begin{alignat}{2}
::<math>\begin{alignat}{2}
[\theta_{L},\theta_{U}]&= \hat{\theta}exp(\pm 1.96\times \frac{se_{\hat{\theta}}}{\hat{\theta}})\\
[\theta_{L},\theta_{U}]&= \hat{\theta}exp\left(\pm 1.96\times \frac{se_{\hat{\theta}}}{\hat{\theta}}\right)\\
&=\left [572.3\times exp \left(-1.96\times\tfrac{41.72}{572.3}\right),572.3\times exp \left(1.96\times\tfrac{41.72}{572.3}\right)\right]\\
&= \left[572.3\times exp \left(-1.96\times\frac{41.72}{572.3}\right),572.3\times exp \left(1.96\times\frac{41.72}{572.3}\right)\right]\\
&= [496,660]\\
&= [496,660]\\
\end{alignat}</math>
\end{alignat}</math>
Line 73: Line 75:
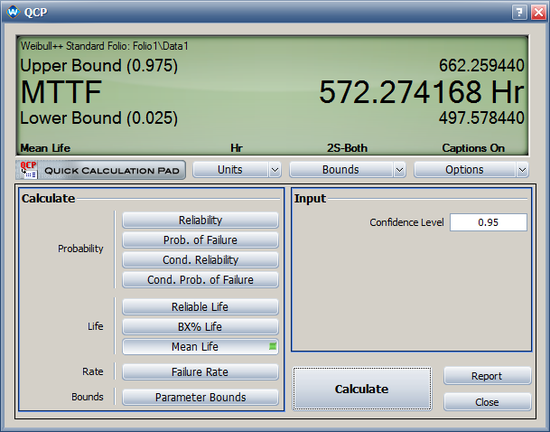
* Based on the likelihood ratio (Select LRB for the confidence bound), the confidence interval is:
* Based on the likelihood ratio (Select LRB for the confidence bound), the confidence interval is:


[[Image:1PE_interval_data.png|center]]
[[Image:1PE_interval_data_qcp.png|center|550 px]]




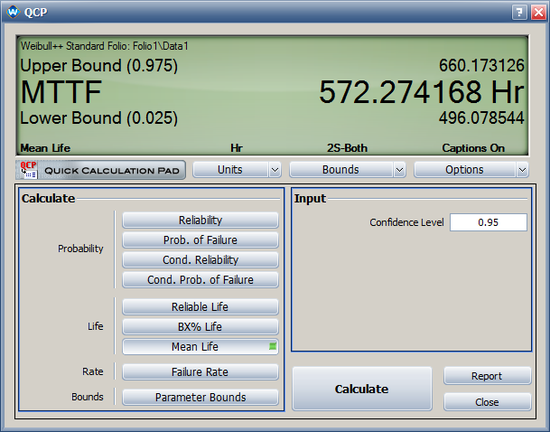
* Based on lognormal approximation (select FM for the bound method), the confidence bounds are:  
* Based on lognormal approximation (select FM for the bound method), the confidence bounds are:  


::<math>\begin{alignat}{2}
[[Image:1PE_interval_data_qcp_FM.png|center|550 px]]
[\theta_{L},\theta_{U}]&= \hat{\theta}exp\left(\pm 1.96 \times \frac{se_{\hat{\theta}}}{\hat{\theta}}\right)\\
&= \left[572.3 \times exp\left(- 1.96 \times \frac{40.466}{572.3}\right), 572.3 \times exp\left(1.96 \times \frac{40.466}{572.3}\right)\right]\\
&= [498, 657]\\
\end{alignat}</math>

Latest revision as of 16:16, 28 September 2015

Weibull Reference Examples Banner.png


New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.



1P-Exponential MLE Solution for Interval Data

This example validates the calculations for the MLE solution, likelihood ratio bound and Fisher Matrix bound for a 1-parameter exponential distribution with interval data in Weibull++ standard folios.


Reference Case

Example 7.1 on page 154 in the book Statistical Methods for Reliability Data by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998. The sample size of 200 data is used here.


Data

Number in State Last Inspected State F/S State End Time
41 0 F 100
44 100 F 300
24 300 F 500
32 500 F 700
29 700 F 1000
21 1000 F 2000
9 2000 F 4000


Result

The cumulative distribution function for an exponential distribution is:

[math]\displaystyle{ F(t)=1-e^{-\left( \frac{t}{\theta }\right )}\,\! }[/math]


The ML estimate [math]\displaystyle{ \hat{\theta}\,\! }[/math] = 572.3, and the standard deviation is [math]\displaystyle{ se_{\hat\theta}\,\! }[/math] = 41.72. Therefore the variance is 1740.56.


The 95% 2-sided confidence interval for [math]\displaystyle{ {\theta}\,\! }[/math] are:

  • Based on the likelihood ratio, the confidence interval is [498, 662]. The calculation is based on
[math]\displaystyle{ -2ln\left [ \frac{L(\theta)}{L(\hat{\theta})} \right ] = X^{2}_{(0.90,1)}\,\! }[/math]


The two solutions of [math]\displaystyle{ \theta\,\! }[/math] in the above equation will be the confidence bounds for [math]\displaystyle{ \theta\,\! }[/math].


  • Based on lognormal approximation, the confidence interval is [496, 660]. The calculation is:
[math]\displaystyle{ \begin{alignat}{2} [\theta_{L},\theta_{U}]&= \hat{\theta}exp\left(\pm 1.96\times \frac{se_{\hat{\theta}}}{\hat{\theta}}\right)\\ &= \left[572.3\times exp \left(-1.96\times\frac{41.72}{572.3}\right),572.3\times exp \left(1.96\times\frac{41.72}{572.3}\right)\right]\\ &= [496,660]\\ \end{alignat} }[/math]


Results in Weibull++


The ML estimator for [math]\displaystyle{ \theta\,\! }[/math] and its variance are 572.27 and 1740.52, respectively. They are given below.

1PE interval data.png

The ML estimator for [math]\displaystyle{ \theta\,\! }[/math] and the variance are the same as the values given in the book.


The 95% 2-sided confidence interval for [math]\displaystyle{ \theta\,\! }[/math] are:

  • Based on the likelihood ratio (Select LRB for the confidence bound), the confidence interval is:
1PE interval data qcp.png


  • Based on lognormal approximation (select FM for the bound method), the confidence bounds are:
1PE interval data qcp FM.png
Retrieved from "https://www.reliawiki.com/index.php?title=1P-Exponential_MLE_Solution_for_Interval_Data&oldid=60808"