Temperature-Nonthermal (TNT)-Weibull Model: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
Kate Racaza (talk | contribs) No edit summary |
||
| (14 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Reference Example|{{Banner ALTA Reference Examples}}}} | {{Reference Example|{{Banner ALTA Reference Examples}}}} | ||
This example | This example validates the calculations for the temperature-nonthermal life-stress relationship with a Weibull distribution in ALTA standard folios. | ||
| Line 105: | Line 105: | ||
*The maximum likelihood estimation (MLE) results for the parameters are: <math>\,\!\alpha _{0}=0.671</math> , <math>\,\!\alpha _{1}=4640.1</math> , <math>\,\!\alpha _{2}=-0.445</math> and <math>\,\!\beta =1.805</math>. | *The maximum likelihood estimation (MLE) results for the parameters are: <math>\,\!\alpha _{0}=0.671</math> , <math>\,\!\alpha _{1}=4640.1</math> , <math>\,\!\alpha _{2}=-0.445</math> and <math>\,\!\beta =1.805</math>. | ||
*The eta parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as <math>\,\!4.244\times 10^{6}</math>. | *The <math>\,\!\eta</math> parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as <math>\,\!4.244\times 10^{6}</math>. | ||
*The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992. | *The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992. | ||
| Line 114: | Line 114: | ||
{{Reference_Example_Heading4|ALTA}} | {{Reference_Example_Heading4|ALTA}} | ||
We will first perform the analysis using the general log-linear (GLL) life-stress relationship, and then compare its results with the temperature-nonthermal (TNT) life-stress relationship. | |||
'''General Log-Linear (GLL)-Weibull Model''' | |||
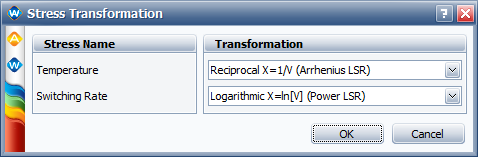
To use the GLL-Weibull model with the same life-stress relationship as the one in the book, the following stress transformations should be used: | |||
[[image:Two Stress GLL Weibull_Stress Transform.png|center]] | [[image:Two Stress GLL Weibull_Stress Transform.png|center]] | ||
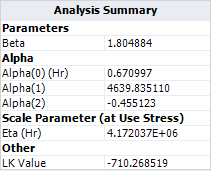
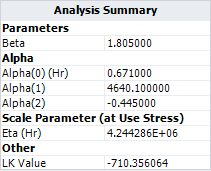
Based on this model, the maximum likelihood estimation (MLE) results for the parameters are: | |||
[[image:Two Stress GLL Weibull_Analysis Summary GLL.png|center]] | [[image:Two Stress GLL Weibull_Analysis Summary GLL.png|center]] | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">'''Results in ALTA'''</div> | |||
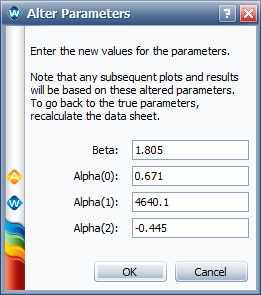
These results are slightly different from the results given in the book (especially for <math>\,\!\alpha _{2}</math>). To see what the log likelihood value (LK Value) would be if we used the parameter values in the book, we use the Alter Parameters tool, as shown next. | |||
[[image:Two Stress GLL Weibull_Alter Parameters.png|center]] | |||
The resulting LK Value for the altered parameters is -710.356064, as shown next. | |||
: | [[image:Two Stress GLL Weibull_Analysis Summary GLL new alpha.png|center]] | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">'''Altered Parameters'''</div> | |||
This likelihood value is slightly smaller than the value that was originally calculated in ALTA, which was -710.268519. Therefore, the result in ALTA is better in terms of maximizing the log likelihood value. | |||
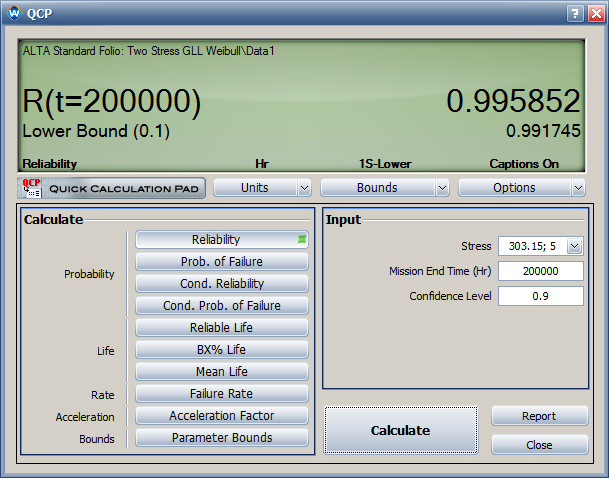
Using the parameters originally calculated in ALTA: | |||
*The <math>\,\!\eta</math> parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as <math>\,\!4.172\times 10^{6}</math>. | |||
*The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 F) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992. | *The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 F) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992, as shown next. | ||
[[image:Two Stress GLL Weibull_QPC Reliability.png|center]] | [[image:Two Stress GLL Weibull_QPC Reliability.png|center]] | ||
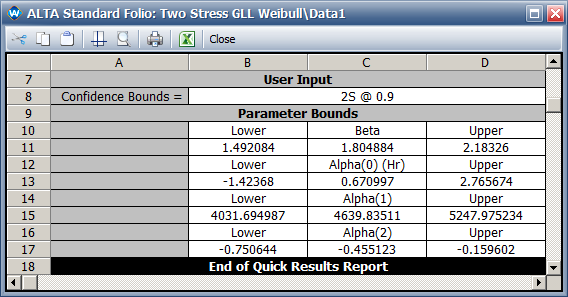
*The two-sided 90% confidence interval for parameter <math>\,\!\alpha _{2}</math> is [-0.751, -0.160]. | *The two-sided 90% confidence interval for parameter <math>\,\!\alpha _{2}</math> is [-0.751, -0.160], as shown next. | ||
[[image:Two Stress GLL Weibull_Parameter Bounds.png|center]] | [[image:Two Stress GLL Weibull_Parameter Bounds.png|center]] | ||
'''Temperature-Nonthermal (TNT)-Weibull Model''' | |||
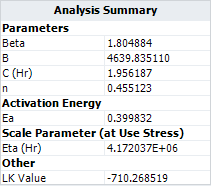
If we use the temperature-nonthermal life-stress relationship to analyze the data, the same results would be obtained, as shown in the following picture. Therefore, by selecting the appropriate stress transformations, a general log-linear model can become a temperature-nonthermal model. | |||
[[image:Two Stress GLL Weibull_Analysis Summary TNT.png|center]] | [[image:Two Stress GLL Weibull_Analysis Summary TNT.png|center]] | ||
Latest revision as of 18:21, 28 September 2015
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.