Arrhenius-Lognormal Model: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
Kate Racaza (talk | contribs) No edit summary |
||
| (12 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Reference Example| | {{Reference Example|{{Banner ALTA Reference Examples}}}} | ||
This example validates the | This example validates the results for the Arrhenius life stress relationship with a Lognormal distribution in ALTA standard folios. | ||
| Line 10: | Line 10: | ||
{{Reference_Example_Heading2}} | {{Reference_Example_Heading2}} | ||
Device | Device A was tested under several different temperature settings. The following table shows the data. | ||
{| {{table}} | {| {{table}} | ||
| Line 93: | Line 93: | ||
| 1||S||5000||353.15||4 | | 1||S||5000||353.15||4 | ||
|} | |} | ||
{{Reference_Example_Heading3}} | {{Reference_Example_Heading3}} | ||
The following function is used for the Ln-Mean <math>\,\!\mu {}'</math> : | The following function is used for the Ln-Mean <math>\,\!\mu {}'</math>: | ||
::<math>\,\!\mu {}'=\beta _{0}+\beta _{1}\times \frac{11605}{T}</math> | ::<math>\,\!\mu {}'=\beta _{0}+\beta _{1}\times \frac{11605}{T}</math> | ||
where ''T'' is the temperature; <math>\,\!\beta _{1}</math> is the activation energy; <math>\,\!11605</math> is from reciprocal of the Boltzmann constant . This function can be written in the following way: | |||
where ''T'' is the temperature; <math>\,\!\beta _{1}</math> is the activation energy; <math>\,\!11605</math> is from the reciprocal of the Boltzmann constant. This function can be written in the following way: | |||
::<math>\,\!e^{{\mu }'}=e^{\alpha _{0}+\frac{\alpha _{1}}{T}}</math> | ::<math>\,\!e^{{\mu }'}=e^{\alpha _{0}+\frac{\alpha _{1}}{T}}</math> | ||
The above equation is the general log-linear model in ALTA. In ALTA, the coefficients are denoted by <math>\,\!\alpha _{i}</math> . | |||
The above equation is the general log-linear model in ALTA. In ALTA, the coefficients are denoted by <math>\,\!\alpha _{i}</math>. | |||
In fact, the above model also can be expressed using the traditional Arrhenius model: | In fact, the above model also can be expressed using the traditional Arrhenius model: | ||
::<math>\,\!e^{{\mu }'}=e^{\alpha _{0}+\frac{\alpha _{1}}{T}}=C\times e^{\frac{B}{T}}</math> | ::<math>\,\!e^{{\mu }'}=e^{\alpha _{0}+\frac{\alpha _{1}}{T}}=C\times e^{\frac{B}{T}}</math> | ||
In the book, the following results are provided: | In the book, the following results are provided: | ||
*ML estimations for the model parameters are: <math>\,\!\sigma =0.98</math> ,<math>\,\!\beta _{0}=-13.469</math> , <math>\,\!\beta _{1}=0.6279</math> (or <math>\,\!\alpha _{1}=7286.78</math>). | |||
*ML estimations for the model parameters are: <math>\,\!\sigma =0.98</math> , <math>\,\!\beta _{0}=-13.469</math> , <math>\,\!\beta _{1}=0.6279</math> (or <math>\,\!\alpha _{1}=7286.78</math>). | |||
*The 95% confidence interval for <math>\,\!\sigma</math> is [0.75, 1.28], for <math>\,\!\beta _{0}</math> is [-19.1, -7.8] and for <math>\,\!\beta _{1}</math> is [0.47, 0.79]. | *The 95% confidence interval for <math>\,\!\sigma</math> is [0.75, 1.28], for <math>\,\!\beta _{0}</math> is [-19.1, -7.8] and for <math>\,\!\beta _{1}</math> is [0.47, 0.79]. | ||
*The variance/covariance matrix for <math>\,\!\sigma</math> , <math>\,\!\beta _{0}</math> and <math>\,\!\beta _{1}</math> is | |||
*The variance/covariance matrix for <math>\,\!\sigma</math> , <math>\,\!\beta _{0}</math> and <math>\,\!\beta _{1}</math> is: | |||
::<math>\,\!\begin{bmatrix} | ::<math>\,\!\begin{bmatrix} | ||
| Line 125: | Line 137: | ||
In terms of <math>\,\!\sigma</math> , <math>\,\!\alpha _{0}</math> and <math>\,\!\alpha _{1}</math>, the variance/covariance matrix is: | :In terms of <math>\,\!\sigma</math> , <math>\,\!\alpha _{0}</math> and <math>\,\!\alpha _{1}</math>, the variance/covariance matrix is: | ||
:<math>\,\!\begin{bmatrix} | |||
::<math>\,\!\begin{bmatrix} | |||
0.0176 & -0.195 & 68.4695\\ | 0.0176 & -0.195 & 68.4695\\ | ||
-0.195 & 8.336 & -2773.5950\\ | -0.195 & 8.336 & -2773.5950\\ | ||
68.4695 & -2773.5950 & 929264.5725 | 68.4695 & -2773.5950 & 929264.5725 | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
*The log-likelihood value is -321.7. | |||
{{Reference_Example_Heading4|ALTA}} | |||
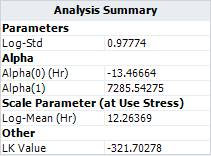
*ML estimations for the model parameters are: | |||
[[image:Arrhenius Lognormal_Analysis Summary.png|center]] | |||
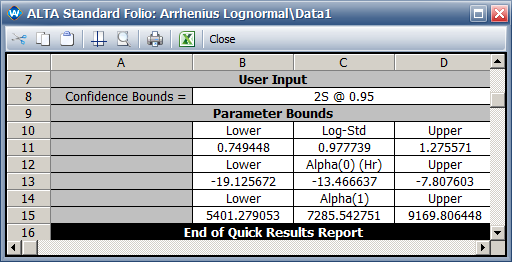
*The 95% confidence intervals are: | |||
[[image:Arrhenius Lognormal_Parameter Bounds.png|center]] | |||
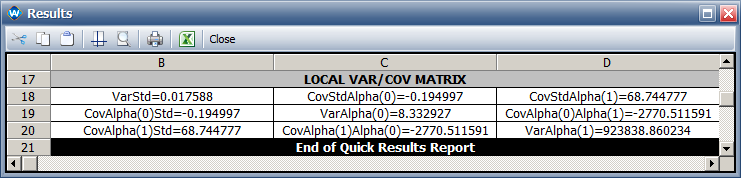
The variance/covariance matrix for <math>\,\!\sigma</math> , <math>\,\!\alpha _{0}</math> and <math>\,\!\alpha _{1}</math> is: | |||
[[image:Arrhenius Lognormal_Var_Cov Results.png|center]] | |||
*The log-likelihood value is -321.7. | |||
It can be seen that all the results in ALTA are very close to the results in the book. | |||
Latest revision as of 18:20, 28 September 2015
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.