General Log-Linear (GLL)-Weibull Model: Difference between revisions
Jump to navigation
Jump to search
(Created page with '{{Reference Example|ALTA_Reference_Examples_Banner.png|ALTA_Reference_Examples}} Validate calculation of GLL relationship for Weibull distribution {{Reference_Example_Heading1}…') |
Kate Racaza (talk | contribs) No edit summary |
||
| (29 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Reference Example| | {{Reference Example|{{Banner ALTA Reference Examples}}}} | ||
This example validates the results for the GLL life-stress relationship with a Weibull distribution in ALTA standard folios. | |||
{{Reference_Example_Heading1}} | {{Reference_Example_Heading1}} | ||
The data set is from Example 7.14 on page 297 in book ''Life Cycle Reliability Engineering'' by Dr. Guangbin Yang, John Wiley & Sons, 2007. | |||
{{Reference_Example_Heading2}} | {{Reference_Example_Heading2}} | ||
The data | The following table shows the data. | ||
{| {{table}} | {| {{table}} | ||
!State F/S | !State F/S | ||
| Line 80: | Line 81: | ||
{{Reference_Example_Heading3}} | |||
The model used in the book is: | |||
::<math>\,\!ln\left ( \eta \right )=\alpha _{0}+\alpha _{1}\frac{1}{T}</math> | |||
{{ | The book has the following results: | ||
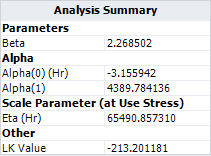
*The model parameters are: <math>\,\!\alpha _{0}=-3.156</math> , <math>\,\!\alpha _{1}=4390</math> and <math>\,\!\beta =2.27</math>. | |||
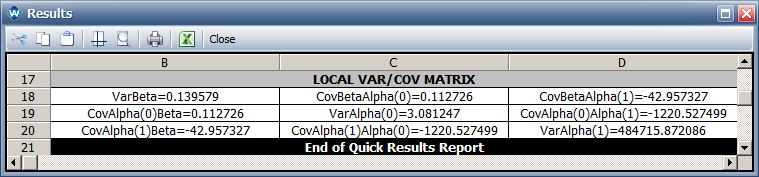
*The variance of each parameter is: <math>\,\!Var\left ( \alpha _{0} \right )=3.08</math> , <math>\,\!Var\left ( \alpha _{1} \right )=484819.5</math> and <math>\,\!Var\left ( \beta\right )=0.1396</math> . | |||
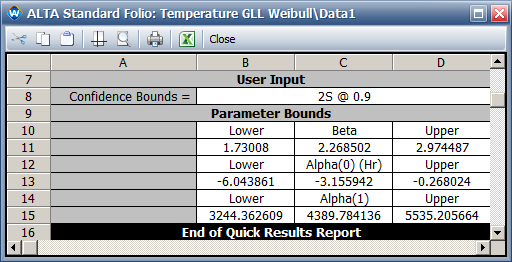
*The two-sided 90% confidence intervals for the model parameters are: <math>\,\!\left [ \alpha _{0,L},\alpha _{0,U} \right ]=\left [ -6.044, -0.269 \right ]</math> , <math>\,\!\left [ \alpha _{1,L},\alpha _{1,U} \right ]=\left [ 3244.8, 5535.3 \right ]</math> and <math>\,\!\left [ \beta _{1,L},\beta _{1,U} \right ]=\left [ 1.73, 2.97 \right ]</math> . | |||
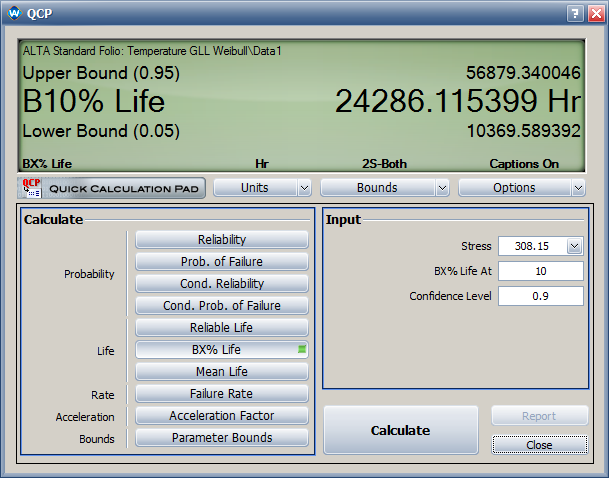
*The estimated B10 life at temperature of 35°C is 24,286 hours. The two-sided 90% confidence interval is [10371, 56867]. | |||
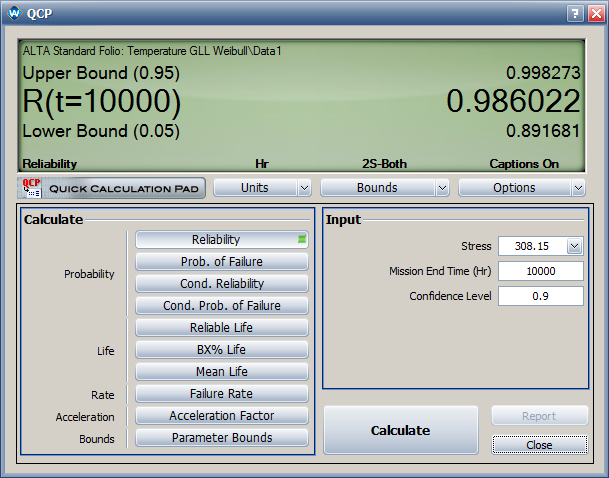
*The estimated reliability at 35°C and 10,000 hours is <math>\,\!R\left ( 10000 \right )=0.9860</math> . The two-sided 90% confidence interval is [0.892, 0.998]. | |||
{{Reference_Example_Heading4|ALTA}} | {{Reference_Example_Heading4|ALTA}} | ||
In ALTA, the GLL model with Weibull distribution is used. Since temperature is the stress, the reciprocal transform is used. The results are: | |||
*The model parameters are: | |||
[[image:Temperature GLL Weibull_Analysis Summary.png|center]] | |||
*The variances of the parameters are: | |||
[[image:Temperature GLL Weibull_Var_Cov Results.png|center]] | |||
*The two-sided 90% confidence intervals for the model parameters are: | |||
[[image:Temperature GLL Weibull_Parameter Bounds.png|center]] | |||
*The estimated B10 life and its two-sided 90% confidence intervals are: | |||
[[image:Temperature GLL Weibull_QPC B10 Life.png|center]] | |||
*The estimated reliability with its two-sided 90% confidence interval at 35°C and 10,000 hours are: | |||
[[image:Temperature GLL Weibull_QPC Reliability.png|center]] | |||
Latest revision as of 18:21, 28 September 2015
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.