Test-Fix-Test Data Reference Example: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
Kate Racaza (talk | contribs) No edit summary |
||
| (33 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Reference Example| | {{Reference Example|{{Banner RGA Reference_Examples}}|Test-Fix-Test Data}} | ||
This example validates the results for test-fix-test data (time terminated) in RGA. | |||
This example | |||
| Line 7: | Line 6: | ||
Crow, L.H., ''Confidence Interval Procedures for the Weibull Process with Applications to Reliability Growth'', U.S. Army Material Systems Analysis Activity, 1981. | Crow, L.H., ''Confidence Interval Procedures for the Weibull Process with Applications to Reliability Growth'', U.S. Army Material Systems Analysis Activity, 1981. | ||
For this example, the following will be calculated: | |||
*Parameters of the Crow-AMSAA (NHPP) model | |||
*Demonstrated MTBF (DMTBF) | |||
*80% two-sided confidence bounds on the DMTBF | |||
{{Reference_Example_Heading2}} | {{Reference_Example_Heading2}} | ||
The following table shows the data. | |||
{| {{table|12%}} | |||
|- | |||
| 0.2 | |||
|- | |||
| 4.2 | |||
|- | |||
| 4.5 | |||
|- | |||
| 5 | |||
|- | |||
| 5.4 | |||
|- | |||
| 6.1 | |||
|- | |||
| 7.9 | |||
|- | |||
| 14.8 | |||
|- | |||
| 19.2 | |||
|- | |||
| 48.6 | |||
|- | |||
| 85.8 | |||
|- | |||
| 108.9 | |||
|- | |||
| 127.2 | |||
|- | |||
| 129.8 | |||
|- | |||
| 150.1 | |||
|- | |||
| 159.7 | |||
|- | |||
| 227.4 | |||
|- | |||
| 244.7 | |||
|- | |||
| 262.7 | |||
|- | |||
| 315.3 | |||
|- | |||
| 329.6 | |||
|- | |||
| 404.3 | |||
|- | |||
| 486.2 | |||
|- | |||
|+'''Termination Time = 500 hours''' | |||
|} | |||
{{Reference_Example_Heading3}} | {{Reference_Example_Heading3}} | ||
{{Reference_Example_Heading4| | The book has the following results: | ||
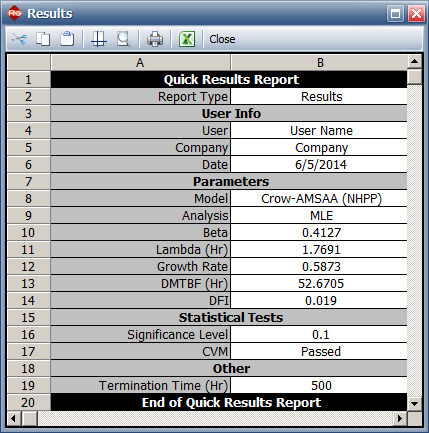
*Beta = 0.413, Lambda = 1.769 | |||
*DMTBF = 52.7 | |||
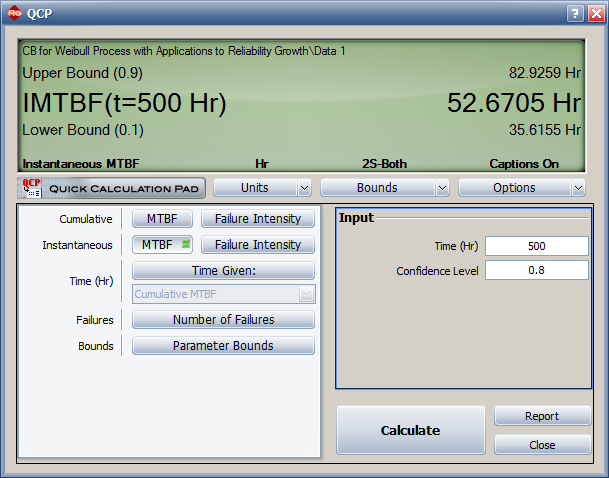
*Confidence Bounds on DMTBF (CL = 80%) = (35.6, 82.9) | |||
{{Reference_Example_Heading4|RGA}} | |||
In RGA, the Crow-AMSAA (NHPP) model with the maximum likelihood estimation (MLE) method was used to calculate the results. The following equations are used to calculate <math>\beta\,\!</math> and <math>\lambda\,\!</math>. | |||
::<math>\begin{align} | |||
\hat{\beta }=&\frac{N}{N\ln T^{*}-\underset{i=1}{\overset{N}{\mathop \sum }}\,T_{i}}\\ | |||
\\ | |||
=&\frac{23}{{23\cdot \ln \left ( 500 \right )}-87.2106}\\ | |||
\\ | |||
=&0.4127 | |||
\end{align}\,\!</math> | |||
::<math>\begin{align} | |||
\hat{\lambda }=&\frac{N}{T^{*\beta }}\\ | |||
\\ | |||
=&\frac{23}{500^{0.4127}}\\ | |||
\\ | |||
=&1.7691 | |||
\end{align}\,\!</math> | |||
*The model parameters are: | |||
[[image:CB for Weibull_Results.png|center]] | |||
*The instantaneous MTBF and its two-sided 80% confidence bounds are: | |||
[[image:CB for Weibull_QPC.png|center]] | [[image:CB for Weibull_QPC.png|center]] | ||
Latest revision as of 18:26, 28 September 2015
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.