Lognormal MLE Solution with Right Censored Data: Difference between revisions
Jump to navigation
Jump to search
Kate Racaza (talk | contribs) (Created page with '{{Reference Example}} This example compares the Lognormal MLE solution with Fisher matrix bound for right censored data. {{Reference_Example_Heading1}} The data on page 199 of…') |
Kate Racaza (talk | contribs) No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{Reference Example}} | {{Reference Example}} | ||
This example | This example validates the calculations for the Lognormal MLE solution with Fisher matrix bound for right censored data in Weibull++ standard folios. | ||
{{Reference_Example_Heading1}} | {{Reference_Example_Heading1}} | ||
The data on page 199 of the book ''Statistical Methods for Reliability Data'' by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998 is used. | The data set on page 199 of the book ''Statistical Methods for Reliability Data'' by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998 is used. | ||
| Line 33: | Line 33: | ||
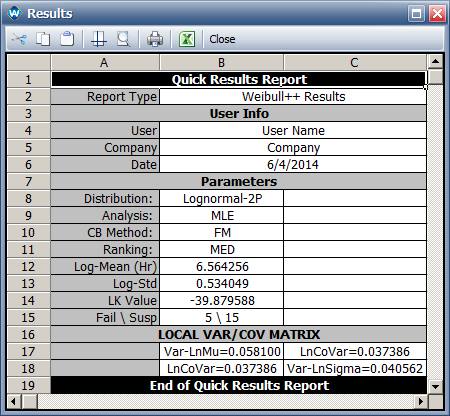
* The MLE solution is <math>\hat{\mu} = 6.56, \ \hat{\sigma} = 0.543\,\!</math>. | * The MLE solution is <math>\hat{\mu} = 6.56, \ \hat{\sigma} = 0.543\,\!</math>. | ||
* The variance and covariance matrix is | * The variance and covariance matrix is | ||
| Line 46: | Line 45: | ||
* The MLE solution and the variance/covariance matrix: | * The following picture shows the MLE solution and the variance/covariance matrix: | ||
[[Image:Lg_right_censored_matrix.png|center]] | [[Image:Lg_right_censored_matrix.png|center]] | ||
* The Fisher matrix bound for parameters: | * The Fisher matrix bound for parameters are: | ||
:For Ln-mu (using normal approximation of Eqn. 8.7 on page 187): | :For Ln-mu (using normal approximation of Eqn. 8.7 on page 187): | ||
::<math>[\hat{\mu}'_{L}, \hat{\mu}'_{U}] = \hat{\mu}' \pm z_{(1-\alpha | ::<math>[\hat{\mu}'_{L}, \hat{\mu}'_{U}] = \hat{\mu}' \pm z_{(1-\alpha / 2)}se_{\hat{\mu}'}\,\!</math> | ||
| Line 61: | Line 60: | ||
::<math>\begin{alignat}{2} | ::<math>\begin{alignat}{2} | ||
[\hat{\mu}'_{L}, \hat{\mu}'_{U}] =& \hat{\mu}' \pm z_{(1-\alpha | [\hat{\mu}'_{L}, \hat{\mu}'_{U}] =& \hat{\mu}' \pm z_{(1-\alpha /2)}se_{\hat{\mu}'}\\ | ||
=& 6.564256 \pm 1.96 \times (0.0581)^{0.5}\\ | =& 6.564256 \pm 1.96 \times (0.0581)^{0.5}\\ | ||
=& [6.0918, 7.0366933]\\ | =& [6.0918, 7.0366933]\\ | ||
| Line 69: | Line 68: | ||
:For Ln-Std (using log-normal approximation of Eqn. 8.8 on page 188): | :For Ln-Std (using log-normal approximation of Eqn. 8.8 on page 188): | ||
::<math>[\hat{\sigma}'_{L}, \hat{\sigma}'_{U}] = \hat{\sigma}'exp (\pm \frac{z_{(1-\alpha | ::<math>[\hat{\sigma}'_{L}, \hat{\sigma}'_{U}] = \hat{\sigma}'exp (\pm \frac{z_{(1-\alpha /2)}se_{\hat{\sigma}'}}{\hat{\sigma}'})\,\!</math> | ||
| Line 75: | Line 74: | ||
::<math>\begin{alignat}{2} | ::<math>\begin{alignat}{2} | ||
[\hat{\sigma}'_{L}, \hat{\sigma}'_{U}] =& \hat{\sigma}'exp (\pm \frac{z_{(1-\alpha | [\hat{\sigma}'_{L}, \hat{\sigma}'_{U}] =& \hat{\sigma}'exp (\pm \frac{z_{(1-\alpha /2)}se_{\hat{\sigma}'}}{\hat{\sigma}'})\\ | ||
=& 0.534049 \times exp(\pm \tfrac{1.96\times 0.040562^{0.5}}{0.534049})\\ | =& 0.534049 \times exp(\pm \tfrac{1.96\times 0.040562^{0.5}}{0.534049})\\ | ||
=& [0.255, 1.118]\\ | =& [0.255, 1.118]\\ | ||
| Line 81: | Line 80: | ||
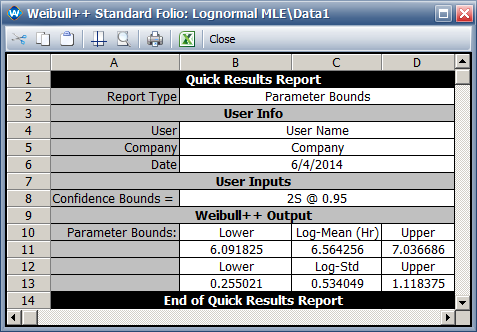
:The results in Weibull++ | :The following picture shows the results in Weibull++: | ||
[[Image:Lg_right_censored_bounds.png|center]] | [[Image:Lg_right_censored_bounds.png|center]] | ||
Latest revision as of 16:18, 28 September 2015
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.