Probability Plotting Example: Difference between revisions
Lisa Hacker (talk | contribs) No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| (12 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner Weibull Examples}} | <noinclude>{{Banner Weibull Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/life_data_analysis Life data analysis reference] and in the [https://help.reliasoft.com/reference/accelerated_life_testing_data_analysis Accelerated life testing reference]''. | ||
</noinclude> | </noinclude> | ||
Let's assume six identical units are reliability tested at the same application and operation | Let's assume six identical units are reliability tested at the same application and operation | ||
stress levels. All of these units fail during the test after operating for the following times (in hours): 96, 257, 498, 763, 1051 and 1744. | stress levels. All of these units fail during the test after operating for the following times (in hours): 96, 257, 498, 763, 1051 and 1744. | ||
The steps for using the probability plotting method to determine the parameters of the exponential | The steps for using the probability plotting method to determine the parameters of the exponential ''pdf'' representing the | ||
data are as follows: | data are as follows: | ||
| Line 11: | Line 11: | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
\text{ | \text{Failure} & \text{Failure Order Number} \\ | ||
\text{ | \text{Time (Hr)} & \text{out of a Sample Size of 6} \\ | ||
\text{96} & \text{1} \\ | \text{96} & \text{1} \\ | ||
\text{257} & \text{2} \\ | \text{257} & \text{2} \\ | ||
| Line 19: | Line 19: | ||
\text{1,051} & \text{5} \\ | \text{1,051} & \text{5} \\ | ||
\text{1,744} & \text{6} \\ | \text{1,744} & \text{6} \\ | ||
\end{matrix}</math></center> | \end{matrix}\,\!</math></center> | ||
Obtain their median rank plotting positions. Median rank positions are used instead of other ranking methods because median ranks are at a | Obtain their median rank plotting positions. Median rank positions are used instead of other ranking methods because median ranks are at a | ||
| Line 27: | Line 27: | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
\text{ | \text{Failure} & \text{Median} \\ | ||
\text{ | \text{Time (Hr)} & \text{Rank, }% \\ | ||
\text{96} & \text{10}\text{.91} \\ | \text{96} & \text{10}\text{.91} \\ | ||
\text{257} & \text{26}\text{.44} \\ | \text{257} & \text{26}\text{.44} \\ | ||
| Line 35: | Line 35: | ||
\text{1,051} & \text{73}\text{.56} \\ | \text{1,051} & \text{73}\text{.56} \\ | ||
\text{1,744} & \text{89}\text{.10} \\ | \text{1,744} & \text{89}\text{.10} \\ | ||
\end{matrix}</math></center> | \end{matrix}\,\!</math></center> | ||
On an exponential probability paper, plot the times on the x-axis and their corresponding | On an exponential probability paper, plot the times on the x-axis and their corresponding | ||
| Line 41: | Line 41: | ||
paper is simply a log-linear paper. | paper is simply a log-linear paper. | ||
[[ | [[Image:ALTA4.1.png|center|500px]] | ||
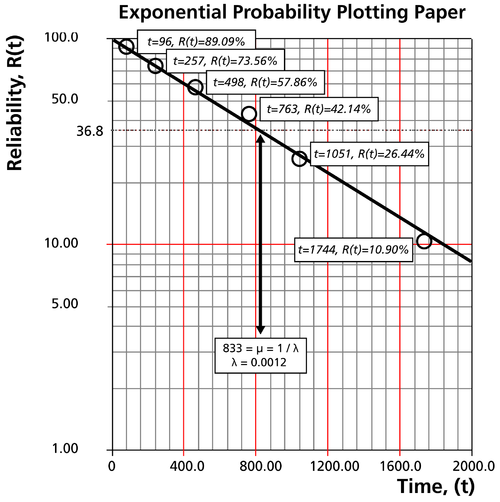
Draw the best possible straight line that goes through the | Draw the best possible straight line that goes through the <math>t=0\,\!</math> and <math> | ||
(t)=100%</math> | (t)=100%\,\!</math> point and through the plotted points (as shown in the plot below). | ||
At the | At the <math>Q(t)=63.2%\,\!</math> or <math>R(t)=36.8%\,\!</math> ordinate point, draw a | ||
straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of the mean. For this case, | straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of the mean. For this case, <math>\widehat{\mu }=833\,\!</math> hours which means that <math>\lambda =\tfrac{1}{\mu }=0.0012\,\!</math> (This is always at 63.2% because <math>(T)=1-{{e}^{-\tfrac{\mu }{\mu }}}=1-{{e}^{-1}}=0.632=63.2%)\,\!</math>. | ||
[[ | [[Image:ALTA4.2.png|center|500px]] | ||
Now any reliability value for any mission time | Now any reliability value for any mission time <math>t\,\!</math> can be obtained. For example, the | ||
reliability for a mission of 15 | reliability for a mission of 15 hours, or any other time, can now be obtained either from the plot or analytically. | ||
To obtain the value from the plot, draw a vertical line from the abscissa, at | To obtain the value from the plot, draw a vertical line from the abscissa, at <math>t=15\,\!</math> | ||
hours, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read | |||
<math>R(t)</math> . In this case, | <math>R(t)\,\!</math>. In this case, <math>R(t=15)=98.15%\,\!</math>. This can also be obtained | ||
analytically, from the exponential reliability function. | analytically, from the exponential reliability function. | ||
Latest revision as of 18:33, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life data analysis reference and in the Accelerated life testing reference.
Let's assume six identical units are reliability tested at the same application and operation stress levels. All of these units fail during the test after operating for the following times (in hours): 96, 257, 498, 763, 1051 and 1744.
The steps for using the probability plotting method to determine the parameters of the exponential pdf representing the data are as follows:
Rank the times-to-failure in ascending order as shown next.
Obtain their median rank plotting positions. Median rank positions are used instead of other ranking methods because median ranks are at a specific confidence level (50%).
The times-to-failure, with their corresponding median ranks, are shown next:
On an exponential probability paper, plot the times on the x-axis and their corresponding rank value on the y-axis. The next figure displays an example of an exponential probability paper. The paper is simply a log-linear paper.
Draw the best possible straight line that goes through the [math]\displaystyle{ t=0\,\! }[/math] and [math]\displaystyle{ (t)=100%\,\! }[/math] point and through the plotted points (as shown in the plot below).
At the [math]\displaystyle{ Q(t)=63.2%\,\! }[/math] or [math]\displaystyle{ R(t)=36.8%\,\! }[/math] ordinate point, draw a straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of the mean. For this case, [math]\displaystyle{ \widehat{\mu }=833\,\! }[/math] hours which means that [math]\displaystyle{ \lambda =\tfrac{1}{\mu }=0.0012\,\! }[/math] (This is always at 63.2% because [math]\displaystyle{ (T)=1-{{e}^{-\tfrac{\mu }{\mu }}}=1-{{e}^{-1}}=0.632=63.2%)\,\! }[/math].
Now any reliability value for any mission time [math]\displaystyle{ t\,\! }[/math] can be obtained. For example, the reliability for a mission of 15 hours, or any other time, can now be obtained either from the plot or analytically.
To obtain the value from the plot, draw a vertical line from the abscissa, at [math]\displaystyle{ t=15\,\! }[/math] hours, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read [math]\displaystyle{ R(t)\,\! }[/math]. In this case, [math]\displaystyle{ R(t=15)=98.15%\,\! }[/math]. This can also be obtained analytically, from the exponential reliability function.