2P Exponential Example: Difference between revisions
Kate Racaza (talk | contribs) (Started review. Will need theory input) |
Lisa Hacker (talk | contribs) No edit summary |
||
| (6 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner Weibull Examples}}[ | <noinclude>{{Banner Weibull Examples}} | ||
'''2 Parameter Exponential | ''This example also appears in the [https://help.reliasoft.com/reference/life_data_analysis Life data analysis reference]''. | ||
</noinclude> | |||
'''2-Parameter Exponential RRY Example'''<br> | |||
14 units were being reliability tested and the following life test data were obtained. Assuming that the data follow a 2-parameter exponential distribution, estimate the parameters and determine the correlation coefficient, <math>\rho \,\!</math>, using rank regression on Y (RRY). | |||
{| border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | |||
{|align="center" border= | |||
|- | |- | ||
!colspan="2" style="text-align:center"| Life Test Data | |||
|- | |- | ||
|- align="center" | |- align="center" | ||
| Line 41: | Line 41: | ||
|14 ||100 | |14 ||100 | ||
|} | |} | ||
'''Solution''' | '''Solution''' | ||
Construct | Construct the following table, as shown next. | ||
<center><math>\overset{{}}{\mathop{\text{Table}\text{- Least Squares Analysis}}}\,</math></center> | <center><math>\overset{{}}{\mathop{\text{Table}\text{- Least Squares Analysis}}}\,\,\!</math></center> | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Line 69: | Line 65: | ||
\text{14} & \text{100} & \text{0}\text{.9517} & \text{-3}\text{.0303} & \text{10000} & \text{9}\text{.1829} & \text{-303}\text{.0324} \\ | \text{14} & \text{100} & \text{0}\text{.9517} & \text{-3}\text{.0303} & \text{10000} & \text{9}\text{.1829} & \text{-303}\text{.0324} \\ | ||
\sum_{}^{} & \text{630} & {} & \text{-13}\text{.2315} & \text{40600} & \text{22}\text{.1148} & \text{-927}\text{.4899} \\ | \sum_{}^{} & \text{630} & {} & \text{-13}\text{.2315} & \text{40600} & \text{22}\text{.1148} & \text{-927}\text{.4899} \\ | ||
\end{matrix}</math></center> | \end{matrix}\,\!</math></center> | ||
The median rank values ( <math>F({{t}_{i}})</math> ) can be found in rank tables or they can be estimated using the '''Quick Statistical Reference | The median rank values ( <math>F({{t}_{i}})\,\!</math> ) can be found in rank tables or they can be estimated using the '''Quick Statistical Reference''' in Weibull++. | ||
Given the values in the table above, calculate <math>\hat{a}</math> and <math>\hat{b}</math>: | Given the values in the table above, calculate <math>\hat{a}\,\!</math> and <math>\hat{b}\,\!</math>: | ||
| Line 80: | Line 76: | ||
\\ | \\ | ||
\hat{b}= & \frac{-927.4899-(630)(-13.2315)/14}{40,600-{{(630)}^{2}}/14} | \hat{b}= & \frac{-927.4899-(630)(-13.2315)/14}{40,600-{{(630)}^{2}}/14} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
or: | or: | ||
::<math>\hat{b}=-0.02711</math> | ::<math>\hat{b}=-0.02711\,\!</math> | ||
and: | and: | ||
::<math>\hat{a}=\overline{y}-\hat{b}\overline{t}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}{N}</math> | ::<math>\hat{a}=\overline{y}-\hat{b}\overline{t}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}{N}\,\!</math> | ||
or: | or: | ||
::<math>\hat{a}=\frac{-13.2315}{14}-(-0.02711)\frac{630}{14}=0.2748</math> | ::<math>\hat{a}=\frac{-13.2315}{14}-(-0.02711)\frac{630}{14}=0.2748\,\!</math> | ||
Therefore: | Therefore: | ||
::<math>\hat{\lambda }=-\hat{b}=-(-0.02711)=0.02711\text{ failures/hour}</math> | ::<math>\hat{\lambda }=-\hat{b}=-(-0.02711)=0.02711\text{ failures/hour}\,\!</math> | ||
and: | and: | ||
::<math>\hat{\gamma }=\frac{\hat{a}}{\hat{\lambda }}=\frac{0.2748}{0.02711}</math> | ::<math>\hat{\gamma }=\frac{\hat{a}}{\hat{\lambda }}=\frac{0.2748}{0.02711}\,\!</math> | ||
or: | or: | ||
::<math>\hat{\gamma }=10.1365\text{ hours}</math> | ::<math>\hat{\gamma }=10.1365\text{ hours}\,\!</math> | ||
Then: | Then: | ||
::<math>f(t)=(0.02711)\cdot {{e}^{-0.02711(T-10.136)}}</math> | ::<math>f(t)=(0.02711)\cdot {{e}^{-0.02711(T-10.136)}}\,\!</math> | ||
The correlation coefficient can be estimated using | The correlation coefficient can be estimated using equation for calculating the correlation coefficient: | ||
::<math>\hat{\rho }=-0.9679</math> | ::<math>\hat{\rho }=-0.9679\,\!</math> | ||
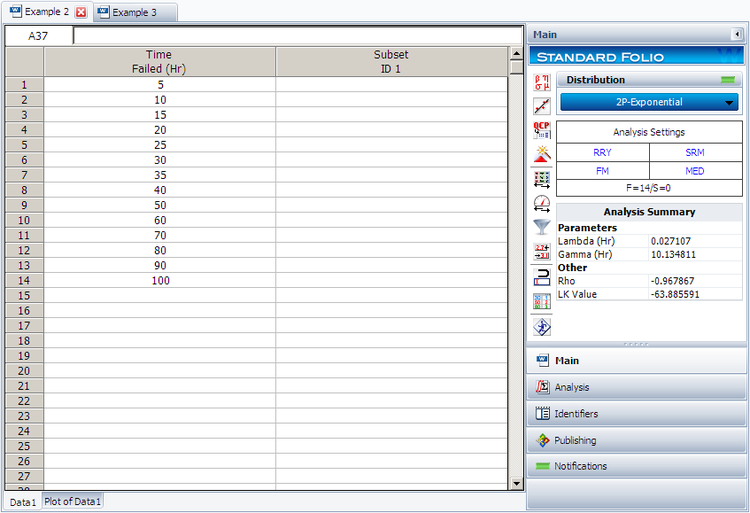
This example can be repeated using Weibull++ | This example can be repeated using Weibull++, choosing 2-parameter exponential and rank regression on Y (RRY), as shown next. | ||
[[Image:Exponential Example 2 Data Folio.png | [[Image:Exponential Example 2 Data Folio.png|center|750px|]] | ||
The estimated parameters and the correlation coefficient using Weibull++ were found to be: | |||
::<math>\hat{\lambda }=0.0271\text{ fr/hr },\hat{\gamma }=10.1348\text{ hr },\hat{\rho }=-0.9679\,\!</math> | |||
Please note that the user must deselect the '''Reset if location parameter > T1 on Exponential''' option on the Calculations page of the Application Setup window. | |||
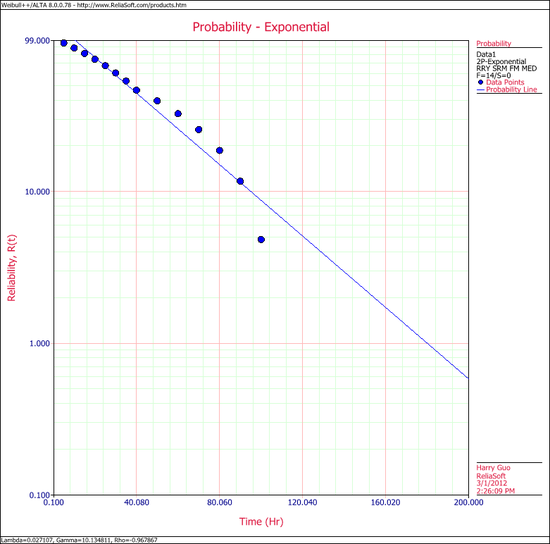
The probability plot can be obtained simply by clicking the '''Plot''' icon. | The probability plot can be obtained simply by clicking the '''Plot''' icon. | ||
[[Image:Exponential Example 2 Plot.png | [[Image:Exponential Example 2 Plot.png|center|550px|]] | ||
Latest revision as of 21:45, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example also appears in the Life data analysis reference.
2-Parameter Exponential RRY Example
14 units were being reliability tested and the following life test data were obtained. Assuming that the data follow a 2-parameter exponential distribution, estimate the parameters and determine the correlation coefficient, [math]\displaystyle{ \rho \,\! }[/math], using rank regression on Y (RRY).
| Life Test Data | |
|---|---|
| Data point index | Time-to-failure |
| 1 | 5 |
| 2 | 10 |
| 3 | 15 |
| 4 | 20 |
| 5 | 25 |
| 6 | 30 |
| 7 | 35 |
| 8 | 40 |
| 9 | 50 |
| 10 | 60 |
| 11 | 70 |
| 12 | 80 |
| 13 | 90 |
| 14 | 100 |
Solution
Construct the following table, as shown next.
The median rank values ( [math]\displaystyle{ F({{t}_{i}})\,\! }[/math] ) can be found in rank tables or they can be estimated using the Quick Statistical Reference in Weibull++.
Given the values in the table above, calculate [math]\displaystyle{ \hat{a}\,\! }[/math] and [math]\displaystyle{ \hat{b}\,\! }[/math]:
- [math]\displaystyle{ \begin{align} \hat{b}= & \frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}}{{y}_{i}}-(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}})(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}})/14}{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,t_{i}^{2}-{{(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}})}^{2}}/14} \\ \\ \hat{b}= & \frac{-927.4899-(630)(-13.2315)/14}{40,600-{{(630)}^{2}}/14} \end{align}\,\! }[/math]
or:
- [math]\displaystyle{ \hat{b}=-0.02711\,\! }[/math]
and:
- [math]\displaystyle{ \hat{a}=\overline{y}-\hat{b}\overline{t}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}{N}\,\! }[/math]
or:
- [math]\displaystyle{ \hat{a}=\frac{-13.2315}{14}-(-0.02711)\frac{630}{14}=0.2748\,\! }[/math]
Therefore:
- [math]\displaystyle{ \hat{\lambda }=-\hat{b}=-(-0.02711)=0.02711\text{ failures/hour}\,\! }[/math]
and:
- [math]\displaystyle{ \hat{\gamma }=\frac{\hat{a}}{\hat{\lambda }}=\frac{0.2748}{0.02711}\,\! }[/math]
or:
- [math]\displaystyle{ \hat{\gamma }=10.1365\text{ hours}\,\! }[/math]
Then:
- [math]\displaystyle{ f(t)=(0.02711)\cdot {{e}^{-0.02711(T-10.136)}}\,\! }[/math]
The correlation coefficient can be estimated using equation for calculating the correlation coefficient:
- [math]\displaystyle{ \hat{\rho }=-0.9679\,\! }[/math]
This example can be repeated using Weibull++, choosing 2-parameter exponential and rank regression on Y (RRY), as shown next.
The estimated parameters and the correlation coefficient using Weibull++ were found to be:
- [math]\displaystyle{ \hat{\lambda }=0.0271\text{ fr/hr },\hat{\gamma }=10.1348\text{ hr },\hat{\rho }=-0.9679\,\! }[/math]
Please note that the user must deselect the Reset if location parameter > T1 on Exponential option on the Calculations page of the Application Setup window.
The probability plot can be obtained simply by clicking the Plot icon.